
§2.2线性方程与常数变易法 ●讲授内容:一阶线性微分方程极其法.Bernoulli方程的解法, 0教学要点:一阶线性微分方程的解法,常数变易法. 例2.12求方程的通解 (+)-w=e(x+为常数. d 例2.13求方程 dx 2x-y 的通解. 例2.14求方程 dy x+y 的通解 d 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 §2.2 线性方程与常数变易法 教学要点: 一阶线性微分方程的解法,常数变易法. 讲授内容: 一阶线性微分方程极其法.Bernoulli方程的解法. 例2.13 求方程 的通解. 2 2 dy y dx x y = − 例2.14 求方程 的通解. 4 3 2 dy x y dx xy + = 例2.12 求方程的通解 n为常数. 1 ( 1) ( 1) dy x n x ny e x dx + + − = +

§2.2线性方程与常数变易法 一阶线性微分方程的标准形式为: (2.19) d .-P(x)y+Q(x) 其中P(x),Q(x)在所讨论的区间上为x的连续函数,当Qx)=0时, (2.19)成为 y =P(x)y (2.20) dx 我们称(2.20)为一阶齐次线性方程.Q(x)≠0时,(2.19)称为线 性非齐次方程,并称Q(x)为线性方程(2.19)的非齐次项.(2.20)的 通解为 P(x)d (2.21) 结束 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 一阶线性微分方程的标准形式为: ( ) ( ) (2.19) dy P x y x dx = +Q 其中P(x),Q(x)在所讨论的区间上为x的连续函数,当Q(x)≡0 时, (2.19)成为 ( ) (2.20) dy P x y dx = 我们称(2.20)为一阶齐次线性方程.Q(x)≠0时,(2.19)称为线 性非齐次方程,并称Q(x)为线性方程(2.19)的非齐次项.(2.20)的 通解为 ( ) (2.21) P x dx y ce = §2.2 线性方程与常数变易法

§2.2线性方程与常数变易法 =P(x)y+Q(x) (2.19) y (2.20) dx dx =P(x)y (2.19)与(2.20)的左端多了一项Qx),我们想,如果(2.21)中的c不是 常数而是x的某个函数,那么y对x导数就会出现两项,因此如果 将c取为适当的函数c(x),那么它有可能满足(2.19)为此,令 y=c(x)elP(o (2.22) 其中cx)为待定函数.要使(2.22)满足(2.21),cc)应取什么样的函 数呢?为此我们将(2.22)及其导数 y(x)=c(P(x)c(x)e 代入(2.19)得 c(x)ec()P(x)e=c(x)P(x)e() 结束 帮助 返回 首页
结束 帮助 上一页 返回 下一页 目录 首页 (2.19)与(2.20)的左端多了一项Q(x),我们想,如果(2.21)中的c不是 常数而是x的某个函数,那么y对x导数就会出现两项,因此如果 将c取为适当的函数c(x),那么它有可能满足(2.19).为此,令 ( ) ( ) (2.22) P x dx y c x e = 其中c(x)为待定函数.要使(2.22)满足(2.21),c(x)应取什么样的函 数呢?为此我们将(2.22)及其导数 ( ) ( ) '( ) '( ) ( ) ( ) P x dx P x dx y x c x e P x c x e = + 代入(2.19)得 §2.2 线性方程与常数变易法 ( ) ( ) (2.19) dy P x y x dx = +Q ( ) (2.20) dy P x y dx = ( ) ( ) ( ) '( ) ( ) ( ) ( ) ( ) ( ) P x dx P x dx P x dx c x e c x P x e c x P x e Q x + = +
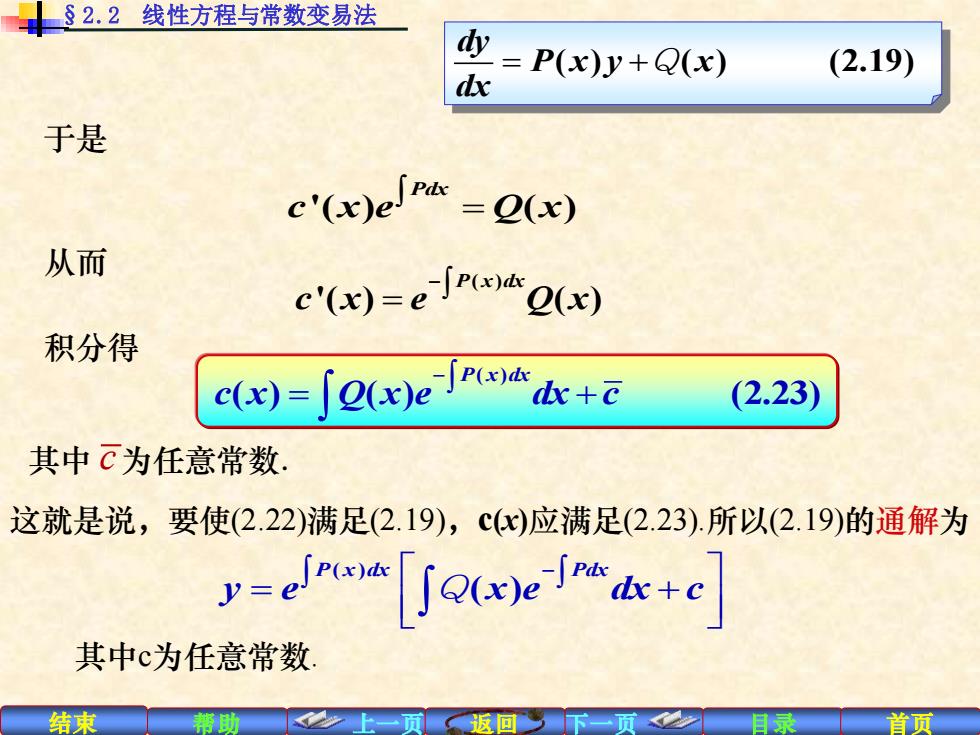
§2.2线性方程与常数变易法 y =P(x)y+Q(x) (2.19) dx 于是 e"(x)e =Q(x) 从而 c"(x)=eQ(x) 积分得 c(e)=∫2()e临+ (2.23) 其中c为任意常数, 这就是说,要使(2.22)满足(2.19),cx)应满足(2.23).所以(2.19)的通解为 y-f Soee 其中c为任意常数 结束 帮助 首页
结束 帮助 上一页 返回 下一页 目录 首页 '( ) ( ) Pdx c x e Q x = 从而 ( ) '( ) ( ) P x dx c x e Q x − = 积分得 ( ) ( ) ( ) (2.23) P x dx c x Q x e dx c − = + 其中 c 为任意常数. §2.2 线性方程与常数变易法 于是 这就是说,要使(2.22)满足(2.19),c(x)应满足(2.23).所以(2.19)的通解为 ( ) ( ) P x dx Pdx y e x e dx c − = + Q 其中c为任意常数. ( ) ( ) (2.19) dy P x y x dx = +Q

§2.2线性方程与常数变易法 以上的方法称为常数变易法。 此外,不难得到方程(2.19)满足y(x。)的解为 edr 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 0 0 0 ( ) ( ) 0 ( ) [ ( ) ] x x x x P t dt P t dt x x y x e y x e dt − = + Q §2.2 线性方程与常数变易法 以上的方法称为常数变易法. 此外,不难得到方程(2.19)满足 y x y ( )0 0 = 的解为
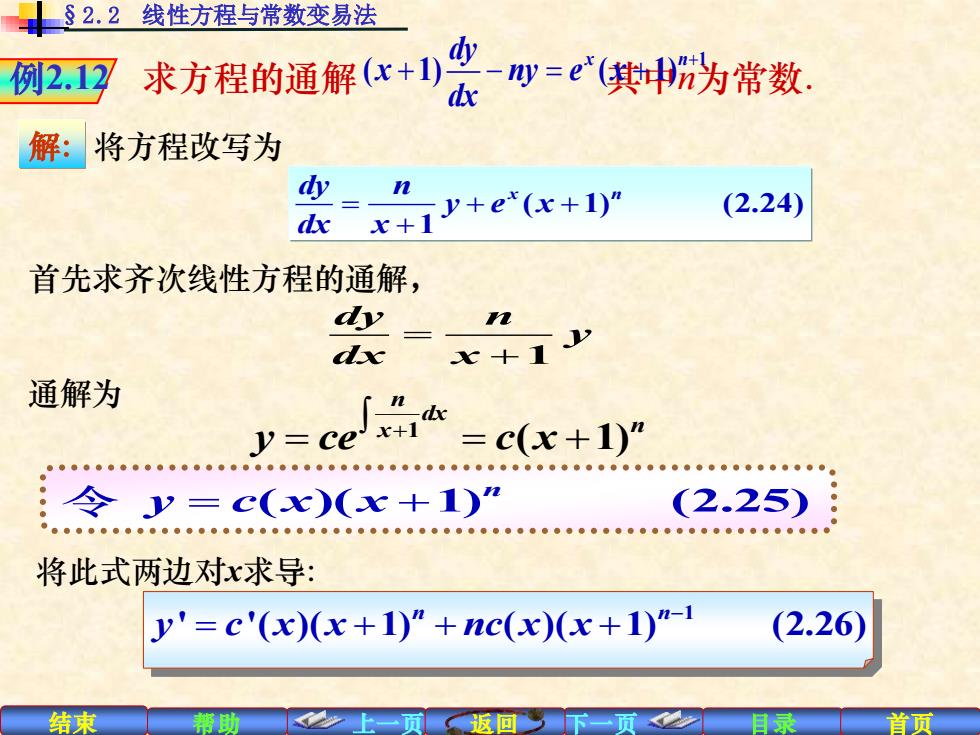
82.2线性方程与常数变易法 例2.12 求方程的通解(x+) -=e(中为常数。 d 解:将方程改写为 =x+ex+) d (2.24) 首先求齐次线性方程的通解, dy 1 dxc r+1少 通解为 y=ce =c(x+1)” 令y=c(x)(x+1)” (2.25) ●● 将此式两边对x求导: y'=c'(x)x+1)”+nc(x)x+1)"- (2.26) 结束 帮助 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 例2.12 求方程的通解 其中n为常数. 1 ( 1) ( 1) dy x n x ny e x dx + + − = + 解: 将方程改写为 ( 1) (2.24) 1 dy n x n y e x dx x = + + + 首先求齐次线性方程的通解, 1 dy n y dx x = + 通解为 1 ( 1) n dx x n y ce c x + = = + ( )( 1) (2.25) n 令 y c x x = + §2.2 线性方程与常数变易法 将此式两边对x求导: 1 ' '( )( 1) ( )( 1) (2.26) n n y c x x nc x x − = + + +
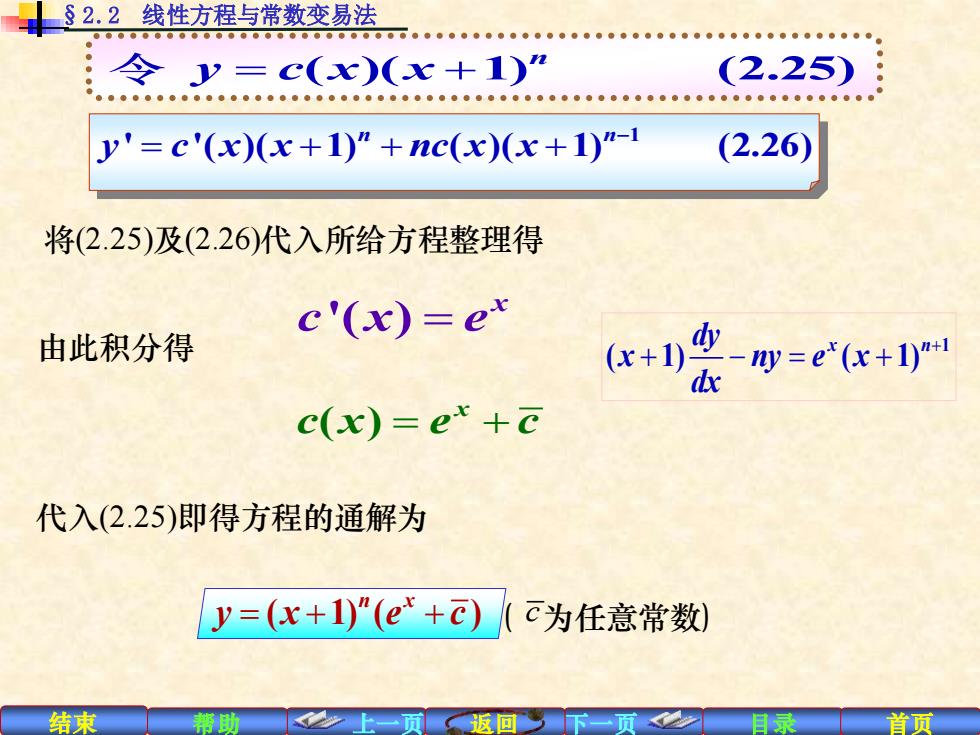
§2.2线性方程与常数变易法 令y=c(x)(x+1)” (2.25) y'=c'(x)(x+1)”+nc(x)(x+1)"-1 (2.26) 将(2.25)及(2.26)代入所给方程整理得 c'(x)=e' 由此积分得 x+项-四=e(x+1 c(x)=ex+c 代入(2.25)即得方程的通解为 y=(c+1)"(e+c)(c为任意常数) 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 '( ) x c x e = 由此积分得 ( ) x c x e c = + 代入(2.25)即得方程的通解为 ( 1) ( ) n x y x e c = + + ( c 为任意常数) §2.2 线性方程与常数变易法 将(2.25)及(2.26)代入所给方程整理得 1 ' '( )( 1) ( )( 1) (2.26) n n y c x x nc x x − = + + + ( )( 1) (2.25) n 令 y c x x = + 1 ( 1) ( 1) dy x n x ny e x dx + + − = +

§2.2线性方程与常数变易法 例2.13求方程 解:原方程不是未知函数y的线性方程但我们可将改写为 dx2x-y'=2 x-y y 把x看成未知函数,而把y看成自变量,这是一个线性方程应 用常数变易法公式,可得原方程的通解为 x=e房产咖+=yre-1nlp 结束 助2上一面扳回下一页<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 例2.13 求方程 的通解 2 . 2 dy y dx x y = − 解: 原方程不是未知函数 y 的线性方程.但我们可将改写为 2 dx x y 2 2 x y dy y y − = = − 把 x 看成未知函数,而把 y 看成自变量,这是一个线性方程.应 用常数变易法公式,可得原方程的通解为 2 2 2 [ ( ) ] ( ln ) dy dy y y x e y e dy c y c y − = − + = − §2.2 线性方程与常数变易法

§2.2线性方程与常数变易法 下面再介绍一种可化为线性方程的方程,它有如下形式 =P()y+2(x)y" (2.27) d 其中Px),Qc)为x的连续函数,n≠0,1为实常数.我们称(2.27) 为Bernoulli方程y≠0时,将(2.27)改写为 y"y'=P(x)y-"+2(x) 于是 1 dyl-n 1-n dx =p(x)y"+2(x) 令z=得” d =1-n)P(x)z+(1-n)2(x) 这是一个关于z的线性方程,由常数变易公式可得通解,然后代回 原来的变量,便得(2.27)的通解.当>0时,Jy=0也是解 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 其中P(x),Q(x)为x的连续函数,n≠0,1为实常数.我们称(2.27) 为Bernoulli方程.y≠0时,将(2.27)改写为 1 ' ( ) ( ) n n y y P x y Q x − − = + 于是 1 1 1 ( ) ( ) 1 n dy n p x y Q x n dx − − = + − 令 得 1 n z y − = (1 ) ( ) (1 ) ( ) dz n P x z n Q x dx = − + − 这是一个关于z的线性方程,由常数变易公式可得通解,然后代回 原来的变量,便得(2.27)的通解.当n>0时, y=0也是解. §2.2 线性方程与常数变易法 下面再介绍一种可化为线性方程的方程,它有如下形式 ( ) ( ) (2.27) dy n P x y Q x y dx = +

S2.2线性方程与常数变易法 y =P(x)y+Q(x)y” (2.27) dx 例2.14 求方程 y 通解。 dx 解:将方程改写为 少_1 =二y+x3y2(这是n=-2时的Bernoulli方程.】 dx x 两端乘y得 y21 y3+x3,即 -3 dx x 3+33 令y°得关于z的一个线性方程 dz =3z+3x3 3 通解为 dx (3xexdx+c)=x(3x+c) 故原方程的通解为. =x3(3x+c):其中c为任意常数 结束 用 上一页返回下一页<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 例2.14 求方程 的通解. 4 3 2 dy x y dx xy + = 解: 将方程改写为 dy 1 3 2 y x y dx x − = + (这是 n =-2时的Bernoulli方程.) 两端乘 得 2 y 2 3 3 1 , dy y y x dx x = + 即 3 3 3 3 3 dy y x dx x = + 令 得关于z的一个线性方程 3 y z = 3 3 3 dz z x dx x = + §2.2 线性方程与常数变易法 ( ) ( ) (2.27) dy n P x y Q x y dx = + 通解为 3 3 3 3 ( 3 ) (3 ) dx dx x x z e x e dx c x x c − = + = + 故原方程的通解为. 3 3 y x x c = + (3 ) 其中c 为任意常数