
常微分方程多媒体教学课件 第二章:一阶微分方程的初等解法 ○第一节变量分离方程与变量变换 ○第二节线性方程与常数变易法 ○第三节恰当方程与积分因子 第四节一阶隐方程与参数表示 。总结 ○本章重点与难点 测试题 结束 帮助 返回下一顶<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 第二章:一阶微分方程的初等解法 常微分方程多媒体教学课件 第一节 变量分离方程与变量变换 第二节 线性方程 与常数变 易法 第三节 恰 当 方 程与 积分 因 子 第四节 一阶隐方程 与 参数表示 本章重点与难点 总结 测试题

第二章一阶微分方程的初等解法 本章介绍一阶方程的初等解法。初等解法也称为初等积 分法。之所以称为初等积分法,是因为这样解法最后都 把求解的问题化成求积分,并将方程的通解用初等函数 或它的积分表达出来。凡是能做到这一点的常微分方程, 称为可积方程。并不是所有的一阶微分方程都是可积的, 即一般的微分方程它没有初等解法。这一章将介绍若干 个可积方程的解法。这些内容虽然简单,但都是常微分 方程求解的基本方法。 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 第二章 一阶微分方程的初等解法 • 本章介绍一阶方程的初等解法。初等解法也称为初等积 分法。之所以称为初等积分法,是因为这样解法最后都 把求解的问题化成求积分,并将方程的通解用初等函数 或它的积分表达出来。凡是能做到这一点的常微分方程, 称为可积方程。并不是所有的一阶微分方程都是可积的, 即一般的微分方程它没有初等解法。这一章将介绍若干 个可积方程的解法。这些内容虽然简单,但都是常微分 方程求解的基本方法

§2.1变量分离方程与变量变换 一.分离变量法 例2.1 例2.2 例2.3 例2.4 二.可化为变量分离方程的方程 例2.5 例2.9 例2.6 例2.10 例2.7 例2.11 例2.8 结束 上一版下而 首页
结束 帮助 上一页 返回 下一页 目录 首页 §2.1 变量分离方程与变量变换 一.分离变量法 二.可化为变量分离方程的方程 例2.1 例2.2 例2.5 例2.3 例2.4 例2.6 例2.9 例2.10 例2.8 例2.7 例2.11
§2.1变量分离方程与变量变换 讲授内容: 1.变量分离方程及其求解方法 2.可化为变量分离的方程 教学要求: 掌握一解变量分离方程求解方法;掌握齐 次方程求解方法. 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 §2.1 变量分离方程与变量变换 1.变量分离方程及其求解方法. 2.可化为变量分离的方程. 掌握一解变量分离方程求解方法;掌握齐 次方程求解方法. 讲授内容: 教学要求:
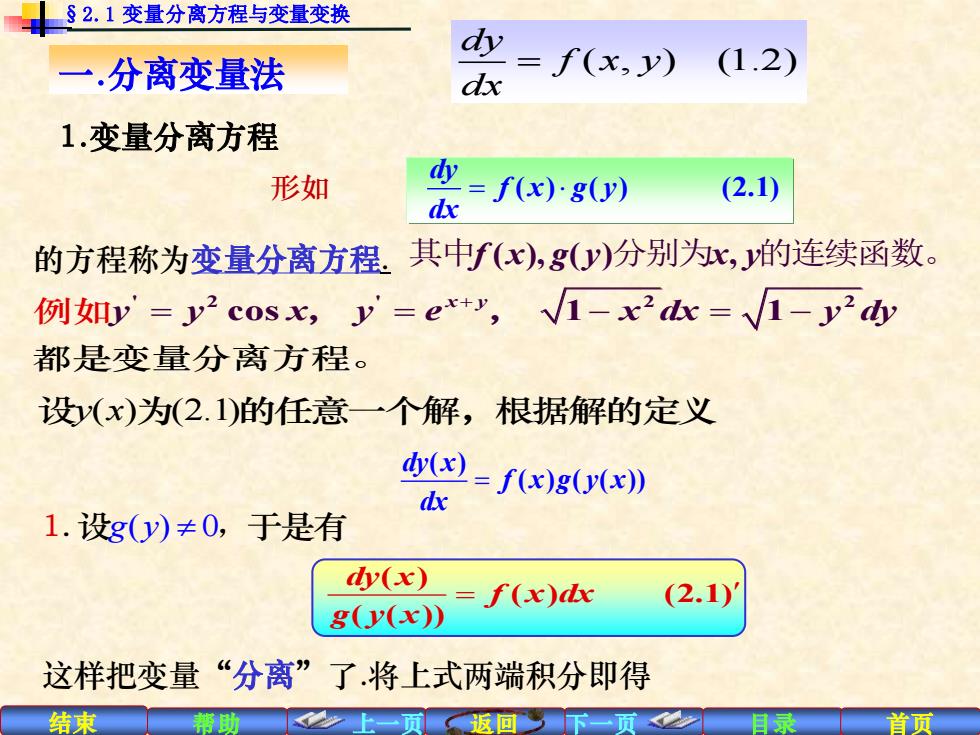
§2.1变量分离方程与变量变换 dy 一.分离变量法 dx .=f(x,y) (1.2) 1.变量分离方程 形如 =f(x)80) d (2.1) 的方程称为变量分离方程。其中f(x),g()分别为r,的连续函数。 例y'=y2cosx,y'=e*+",√1-x2dx=√1-y2y 都是变量分离程。 设(x)为(2.1)的任意一个解,根据解的定义 (x d 2=fx)g(0(x》 1.设g(y)≠0,于是有 dy(x) (2.1) g(v(x)) =f(x)dx 这样把变量“分离”了.将上式两端积分即得 结束 帮助 2一贡返回下页<之 首页
结束 帮助 上一页 返回 下一页 目录 首页 ' 2 ' 2 2 cos 1 1 x y y y x y e x dx y dy + 例如 = = − = − 都是变量分 , , 离方程。 1. 设g y( ) 0 ,于是有 ( ) ( ) (2.1) ( ( )) dy x f x dx g y x = 一.分离变量法 1.变量分离方程 的方程称为变量分离方程. 其中f x g y x y ( ), ( ) , 分别为 的连续函数。 这样把变量“分离”了.将上式两端积分即得 设y x( ) (2.1) 为 的任意一个解,根据解的定义 ( ) ( ) ( ( )) dy x f x g y x dx = §2.1 变量分离方程与变量变换 ( ) ( ) (2.1) dy f x g y dx 形如 = ( , ) (1.2) dy f x y dx =

§2.1变量分离方程与变量变换 dv(x) 「f(x)dk+C(2.2) 8(y(x) 这里C是使得2.2)有意义的任意常数.这说明(2.2)的任意一个解必须满足方程 设 ∫g+c n-·r-eh+C (2.3) 则(2.3)可写为 Φ(y)=F(x)+C (2.4) 下面证明,方程(2.4),既(2.2)存在隐函数yy),它是(2.1)的解。 从而(2.2)是(2.1)的解. 结束 帮助 返正
结束 帮助 上一页 返回 下一页 目录 首页 ( ) ( ) (2.2) ( ( )) dy x f x dx C g y x = + 这里C是使得(2.2)有意义的任意常数.这说明(2.2) 的任意一个解必须满足方程 ( ) ( ) dy f x dx C g y = + ( ) ( ) ( ( )) dy x y g y x = F x f x dx C ( ) ( ) (2.3) = + , = + ( ) ( ) (2.4) y F x C 设 则(2.3)可写为 下面证明,方程(2.4) ,既(2.2)存在隐函数 y=y(x) ,它是(2.1)的解. 从而(2.2) 是(2.1)的解. §2.1 变量分离方程与变量变换

§2.1变量分离方程与变量变换 事实上,由于Fx)gy)连续且g(y)≠0,故由隐函数存在定理,(2.4)存 在唯一的隐函数yyx)连续,可微。 所以D(y(x)=F(x)+C 即 9=∫fx)k+C g(y(x)) 两边对x求导: y(x) =f(x) ()=「(x). g(y(x)) dyo(y(x)) dx 或Jy'(x)=f(x)p(y(x) 这表明y=yx)是(2.1)的解.从而2.4)是(2.1)的解 综上所述,求(2.1)的解的问题就化成了求(2.1)'两端的积分,并从 (2.4)中求yx)的问题。 结束 帮助 上一面意扳同下顶<2必 首页
结束 帮助 上一页 返回 下一页 目录 首页 所以 + ( ( )) ( ) y x F x C 事实上,由于F(x),g(y)连续且g(y)0,故由隐函数存在定理, (2.4)存 在唯一的隐函数 y=y(x) 连续,可微. ( ) ( ) ( ( )) dy x f x dx C g y x + 即 两边对x求导: ' ( ) ( ) ( ( )) y x f x g y x = ' 或 y x f x y x ( ) ( ) ( ( )) = 这表明y=y(x)是(2.1)的解.从而(2.4) 是(2.1)的解. 综上所述,求(2.1)的解的问题就化成了求(2.1)'两端的积分, 并从 (2.4)中求y(x)的问题。 ( ) ( ) ( ( )) ( ( )) d dy x d dy x dy dx y x dy y x dx = ( ) ( ) ( ( )) ( ( )) d dy x d dy x dy dx y x dy y x dx = §2.1 变量分离方程与变量变换

§2.1变量分离方程与变量变换 2.若存在y=yo,使得g(y)=0. 此时y=也是(2.1)的一个解。 所以(2.1)除了通积分(2.2),还可能有一些常数解。 例2.求解方程少 =y2cosx,并求出满足初始条件 y(0)=1的解。 解:首先,将方程分离变量得 y cos xdx (设y≠0) 对两边积分推出 =sinx+c (☒) 这里c为任意常数,但是无论c取怎样的常数值,这个解都 不包含原来方程的解y=0,因而原方程的一切解应由上述 通解和解y=0组成 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 0 0 2. ( ) 0. 若存在y y g y = = ,使得 0 此时y y = 也是(2.1)的一个解。 所以(2.1)除了通积分(2.2),还可能有一些常数解。 2 (0) s 1 2. co dy y x dx y = = 例 1求解方程 ,并求出满足初始条件 的解。 解: 首先,将方程分离变量得 2 cos ( 0) dy xdx y y = 设 对两边积分推出 1 sin ( ) x c y − = + 这里c为任意常数,但是无论c取怎样的常数值,这个解都 不包含原来方程的解 y=0,因而原方程的一切解应由上述 通解和解 y=0组成. §2.1 变量分离方程与变量变换

§2.1变量分离方程与变量变换 其次,为了求出给定初值问题的特解,不难看出解y=0显 然不满足初始条件,因此只能在通解中去找出所需要的解 为此在方程(⑧)中令x=0,Jy=0即得c=-1,于是所求初值问题 的解为 y= 1-sinx 例2.2 求出方程 的通解。 dx 1-x2 解: 显然y=士1是方程的解.令y≠士1,将方程进行变量分离得 1 A-= 1 对两边积分推出 arcsin y=arcsinx+C 结束 上一页返回下一页<2 首页
结束 帮助 上一页 返回 下一页 目录 首页 2 2 2.2 1 1 dy y dx x − = − 例 求出方程 的通解。 2 2 1 1 1 1 dy dx y x = − − 解: 对两边积分推出 显然y=±1是方程的解.令y ±1,将方程进行变量分离得 arcsin arcsin y x C = + 其次,为了求出给定初值问题的特解,不难看出解y=0显 然不满足初始条件,因此只能在通解中去找出所需要的解. 为此在方程()中令x=0, y=0 即得 c= -1,于是所求初值问题 的解为 1 1 sin y x = − §2.1 变量分离方程与变量变换

§2.1变量分离方程与变量变换 其中C为任意常数.因此通解为 y=sin(arcsinx+c) 例2.3 求解方程J+(x2-4x)=0. 解:y=O是方程的解y≠0时,将方程进行变量分离得: 1,k+1d=0 x2-4x 两边积分得 5gix-C 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 y x c = + sin(arcsin ) 其中C为任意常数. 因此通解为 2 1 1 0 4 dx dy x x y + = − 2 0 1 1 ln 4 dx dy C x x y = − + − 2 例2.3 求解方程 ydx x x dy + − = ( 4 ) 0. y=0是方程的解.y 0时,将方程进行变量分离得: 两边积分得 解 : §2.1 变量分离方程与变量变换