
第五意线性微分方程组 §5.1 存在唯一性定理 5.1.1记号和定义 5.1.2存在唯一性定理 §5.2线性微分方程组的一般理论 5.2.1齐线性微分方程组 5.2.2非齐线性微分方程组 §5.3常系数线性微分方程组 5.3.1矩阵指数expA的定义和性质 5.3.2基解矩阵的计算公式 结束 帮助 上一页返回下一页 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 § 5.1 存在唯一性定理 5.1.1 记号和定义 5.1.2 存在唯一性定理 § 5.2 线性微分方程组的一般理论 5.2.1 齐线性微分方程组 5.2.2 非齐线性微分方程组 §5.3 常系数线性微分方程组 5.3.2 基解矩阵的计算公式 5.3.1矩阵指数expA的定义和性质

线性微分方程组 S5.1存在唯一定理 5.1.1记号和定义 在前几章里,我们研究了含有一个未知函数的微方程的 解的性质及解法.但在许多实际问题与理论问题中,还要求 我们去求解含有多个未知函数的微分方程组,或者研究它们 的解的性质. 例如,已知在空间运动的质点在点(x,的速度与时间t及点的坐 标(的焱系为 =f(t,x,y,z) dt y =f3(t,x,y,) dt d dt =f(t,x,y,z) 结束 返回下一页 首页
结束 帮助 上一页 返回 下一页 目录 首页 §5.1 存在唯一定理 在前几章里,我们研究了含有一个未知函数的微方程的 解的性质及解法.但在许多实际问题与理论问题中,还要求 我们去求解含有多个未知函数的微分方程组,或者研究它们 的解的性质. 1 2 3 = = = ( , , , ) ( , , , ) ( , , , ) dx f t x y z dt dy f t x y z dt dz f t x y z dt 线性微分方程组 5.1.1 记号和定义 例如,已知在空间运动的质点在点 的速度与时间t及点的坐 标 的关系为 p x y z ( , , ) ( , , ) x y z

线性微分方程组 且质点在时刻t经过点 (x。,球该质点的运动轨迹.这个问 题其实就是求微分方程组 dx dt f(t,x,y,) y =f2(t,x,y,) dt dz dt =f3(t,x,y,) 满足初始条件 (to)=xo y(to)=yo (to)=o 的解x()y).z) 又如,在第一章,我们讨论过数学摆的运动微分方程为: d'p=-gsinp do dt2 dt 如果令 d9=0则此运动还可用方程组 do 表示 sin@ dt 1 结束 帮助 返回 目录
结束 帮助 上一页 返回 下一页 目录 首页 1 2 3 ( , , , ) ( , , , ) ( , , , ) dx f t x y z dt dy f t x y z dt dz f t x y z dt = = = 又如,在第一章,我们讨论过数学摆的运动微分方程为: 如果令 , 则此运动还可用方程组 d dt = 满足初始条件 2 2 sin d g dt l = − 线性微分方程组 的解 x(t) y(t) . z(t) . 0 0 x t x ( ) = 0 0 y t y ( ) = 0 0 z t z ( ) = 且质点在时刻 经过点 ,求该质点的运动轨迹.这个问 题其实就是求微分方程组 0 t 0 0 0 ( , , ) x y z sin d dt d g dt l = = − 表示

线性微分方程组 在例1和例2中,方程中出现的未知函数的导数都是一阶的.所以称 它们是一阶微分方程组.含有n个未知函数x1,x2,·的阶微分方 程组的一般形式是 dx dt =f(t,x1,x2,.xn) 2=f6,x,x2x) dt a=f() dt 结束 助2上一贡返回下一页<2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 在例1和例2中,方程中出现的未知函数的导数都是一阶的.所以称 它们是一阶微分方程组.含有n个未知函数 的一阶微分方 程组的一般形式是 1 2 , ,. x x xn 1 1 1 2 2 2 1 2 1 2 ( , , ,. ) ( , , ,. ) . ( , , ,. ) n n n n n dx f t x x x dt dx f t x x x dt dx f t x x x dt = = = 线性微分方程组

线性微分方程组 当一个一阶微分方程组关于,X2及,X,x,x,是线性的 时候,这样的方程称为一阶线性方程组.一般形式为: dx dt =a11x1+a12x2+.ainxn+f(t) dx2 dt =a21x1+a22x2+.a2nxn+f2(t) ●●●● ●●●●●● dxn dt =anix1+an2x2+.annxn+f(t) 其中 ai(t) ·(i,j=1,2,m),f(t) (i=1,2,.n) 在a≤t是连续的.在这一章我们着重讨论(5.1)的解的性 质及解的求法, 结束 帮助 返叵
结束 帮助 上一页 返回 下一页 目录 首页 在 上是连续的.在这一章我们着重讨论(5.1)的解的性 质及解的求法. a t b 当一个一阶微分方程组关于 及 是线性的 时候,这样的方程称为一阶线性方程组.一般形式为: 1 2 , ,., n x x x ' ' ' 1 2 , ,., n x x x 1 11 1 12 2 1 1 2 21 1 22 2 2 2 1 1 2 2 . ( ) . ( ) . . ( ) n n n n n n n nn n n dx a x a x a x f t dt dx a x a x a x f t dt dx a x a x a x f t dt = + + + = + + + = + + + 线性微分方程组 ( ) ( , 1,2,., ) i j n = a t ij ( ) i f t 其中 . , ( 1,2,. ) i n =
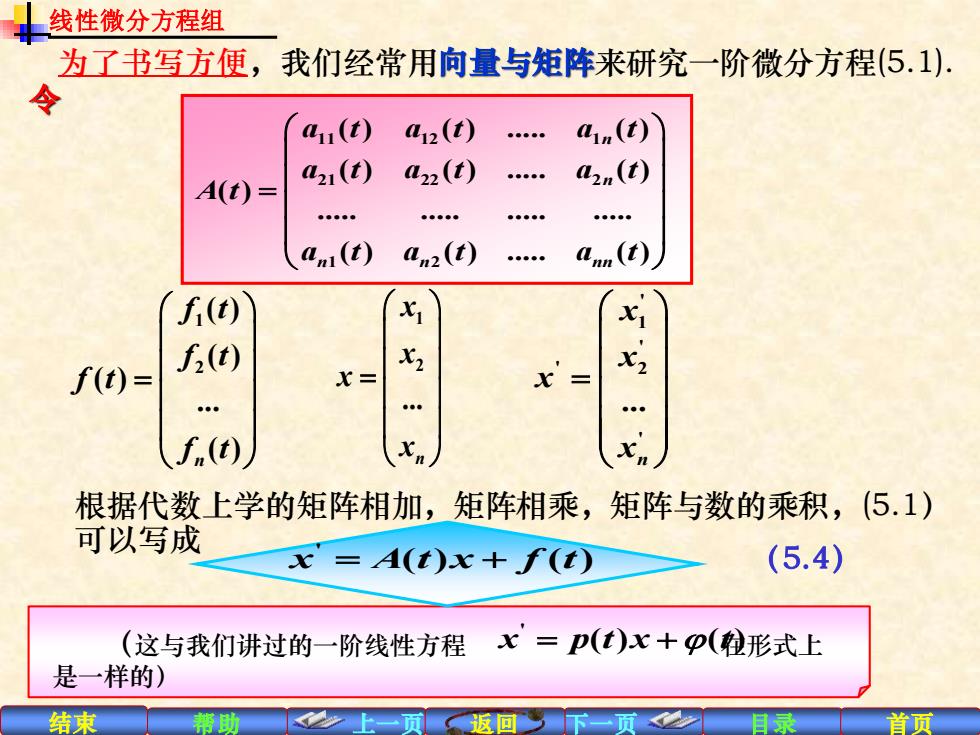
线性微分方程组 为了书写方便,我们经常用向量与矩阵来研究一阶微分方程(5.1) 41u(t) a12(t) ain(t) a21(t) a22(t) A(t)= 2n(t) o.oo ●●◆ ●◆◆●。 am(t) a2(t) aun(t) (t) 1 f2(t) 七32 f(t)= x= X2 (t 根据代数上学的矩阵相加,矩阵相乘,矩阵与数的乘积,(5.1) 可以写成 x=A(t)x+f(t) (5.4) (这与我们讲过的一阶线性方程x=P(t)x+p(粒形式上 是一样的) 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 根据代数上学的矩阵相加,矩阵相乘,矩阵与数的乘积, (5.1)可以写成 (这与我们讲过的一阶线性方程 在形式上 是一样的) ' x p t x t = + ( ) ( ) 11 12 1 21 22 2 1 2 ( ) ( ) . ( ) ( ) ( ) . ( ) ( ) . . . . ( ) ( ) . ( ) n n n n nn a t a t a t a t a t a t A t a t a t a t = 为了书写方便,我们经常用向量与矩阵来研究一阶微分方程(5.1). 令 x A t x f t ' = + ( ) ( ) (5.4) 1 2 ( ) ( ) ( ) . ( ) n f t f t f t f t = ' 1 ' ' 2 ' . n x x x x = 1 2 . n x x x x = 线性微分方程组 根据代数上学的矩阵相加,矩阵相乘,矩阵与数的乘积,(5.1) 可以写成

上线性微分方程组 引进以下概念: 设B)是一个n×矩阵,U()是一个n维列向量, b(t)). bin(t) b21(t) b2n(t) B(t)= U(t)= b(t) bn(t) u, 如果每一个b,淘 [血通续,则称 在B(t)止连续b] 如果每一个山,(相 [姓续,则称 在U()上避续知] 如果每一个b,(和 uxt) 止可,则称 ,B(t)在U(t)上 可做,] B(t) Bi(t) 1 B2 (t) B'(t)= b2() U'()= ●eeee b() B.(t) 如果每一个b,(和 uxt) 衡积,则称 ,B(t)在U(t)上 可换,] 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 引进以下概念:设B(t)是一个 n n 矩阵,U(t)是一个n维列向量. 11 1 21 2 1 ( ) . ( ) ( ) . ( ) ( ) . . . ( ) . ( ) n n n nn b t b t b t b t B t b t b t = 1 : ( ) : n u U t u = 如果每一个 ( ) 在 上连续, 则称 在 B t( ) 上连续. b t ij [ , ] a b [ , ] a b 如果每一个 和 在 上可微,则称 , 在 上 可微,且 ( ) ij b t ( ) u t i [ , ] a b B t( ) U t( ) [ , ] a b ( ) u t i 如果每一个 在 [ , ] a b 上连续,则称 在 U t( ) 上连续 [ , ] a b . 线性微分方程组 11 1 21 2 1 ( ) . ( ) ( ) . ( ) ( ) . . . ( ) . ( ) n n n nn b t b t b t b t B t b t b t = ' 1 ' : ( ) : n u U t u = 如果每一个 和 在 上可积,则称 , 在 上 可积,且 ( ) ij b t ( ) u t i [ , ] a b B t( ) U t( ) [ , ] a b

线性微分方程组 =A(t)x+f(t) (5.4) 广s0h.6.④h ∫。4()t ∫心B0t= ∫a山 .(0t∫bdd ∫n(e) 由定义不难证明,如果A(t),B(t),U(t)在[a,b]上可导,则 【i】(A(t)+B(t))=A(t)+B'(t)(u(t)+v(t)=u(t)+y'(t) 【i】(A(t)×B(t)=A(t)B(t)+A(t)B(t) 【iii】(A(t)u(t))=A'(t)u(t)+A(t)u'(t) 定义:设A(t)是a≤t长的 续矩阵,是f(t)上的连续b维向 量.若存在定义在某区间 [a,B](la,BlCla,bl) 上的连续可微维向量使得在 [止相] u(t)=A(t)u(t)+f(t) 则称U(是(5.4)在 [的B阶解 结束 帮助 <2上一面 返回下<2 首页
结束 帮助 上一页 返回 下一页 目录 首页 定义:设A(t)是 上的 连续矩阵, 是 上的连续 维向 量.若存在定义在某区间 , 上的连续可微 维向量 使得在 上有 n n [ , ] ([ , ] [ , ]) a b a t b f t( ) a t b n n U t( ) [ , ] ' u t A t u t f t ( ) ( ) ( ) ( ) = + 则称 U t( )是(5.4)在 [ , ] 的一个解 由定义不难证明,如果A t B t U t ( ), ( ), ( )在[a,b]上可导,则 【ⅰ】 【ⅱ】 ( ) ' ' ' A t B t A t B t ( ) ( ) ( ) ( ) + = + ( ) ' ' ' u t v t u t v t ( ) ( ) ( ) ( ) + = + ( ) ' ' ' A t B t A t B t A t B t ( ) ( ) ( ) ( ) ( ) ( ) = + 【ⅲ】 ( ) ' ' ' A t u t A t u t A t u t ( ) ( ) ( ) ( ) ( ) ( ) = + 11 1 1 ( ) . ( ) ( ) . . . ( ) . ( ) b b n a a b a b b n nn a a b t dt b t dt B t dt b t dt b t dt = 1 ( ) : ( ) : ( ) b a b a b n a u t dt u t dt u t dt = 线性微分方程组 x A t x f t ' = + ( ) ( ) (5.4)

线性微分方程组 (即存在一组函数41(t),2(),4(),使得 (0=a,(d0u,(0)+aa(04,0+.+an(0u.(④+f: dt (i=1,2,m) 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 1 1 2 2 ( ) ( ) ( ) ( ) ( ) . ( ) ( ) . i i i in n i du t a t u t a t u t a t u t f dt = + + + + (i n = 1,2,., ) (即存在一组函数 u t u t u t 1 2 ( ), ( ),., ( ) n ,使得 线性微分方程组

线性微分方程组 710 称求方程组x()=A()x满忠) 的解的7 7三 720 问题称为初值问题 例:证明u() (到问题 -0小0-( 在区间 (-o,的解 解:uo-( 地处可碍.处处可鼠)且 w-(-0-00o .(是给定初值问题的解。 结束 上一贡返回下页2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 在区间 上的解. 例:证明 ( ) 是初值问题 t t e u t e − = − ' 0 1 1 0 x x = 1 0 1 x( ) = − (− + , ) ' 0 1 1 0 1 ( ) ( ) 0 1 0 t t t t u t u t e e e e − − − − − = = = − ∴ 是给定初值问题的解. u t( ) 称求方程组 满足 的解的 问题称为初值问题. ' x t A t x f t ( ) ( ) ( ) = + 0 x t( ) = 10 20 0 : n = . (0) ∵ 1 处处可导. ∴ 处处可导,且 1 u , = − , t t e e − 解 − u t( ) : 线性微分方程组