
§3.解对初值的连续性和 可微性 讲授内容:解对初值的连续性概念及解对 初值的连续性,可微性定理 讲授要点:解对初值的连续性定理 结束 助2上一贡返回下一页<2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 §3. 解对初值的连续性和 可微性 讲授内容: 解对初值的连续性概念及解对 初值的连续性, 可微性定理 讲授要点: 解对初值的连续性定理

3.3解对初值的连续性和可微性 例:求方程 =y满足yx,)=的解。 d y=ce由y,=ce的满足y(x)=的解为y=ye- 说明解不仅是的函数,而且也是xo,'o的函数.所以 一般地初值问题 [y'=f(x,y) (2.1) y(x)=yo 的解,不仅依赖于x,同时也依赖于初值x) 因此,在初值变化的情况下,初值问题(2.1)的解是x,xo,y 的三元函数.记为 y=e(x,) 满足yo=p(X0,X0,yo) 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 例: 求方程 = 满足 的解 . dy y dx y x y ( ) 0 0 = 0 ( , ) (2.1) ( ) y f x y y x y = = x 0 0 ( , ) x y 0 0 x x y , , 的解,不仅依赖于 ,同时也依赖于初值 . 因此,在初值变化的情况下,初值问题(2.1)的解是 的三元函数.记为 = x y ce = 0 0 x y ce y x y ( ) 0 0 = − = 0 0 x x y y e 0 0 x y, 由 的满足 的解为 说明解不仅是 的函数,而且也是 的函数. 所以 一般地初值问题 x §3.3 解对初值的连续性和可微性 = 0 0 y x x y ( , , ) 满足 y x x y 0 0 0 0 =( , , )

3.3解对初值的连续性和可微性 解关于初值的一些基本性质 解关于初值的对称性: 设(2.1)满足y(x)=y的解是唯一的,记为 y=P(x,xo>Yo) 则在解的存在范围内,有y=p(x,x,y)成立. 事实上,在解的存在区间内任取一值x1,且记 =(x,x,o) 则由解的唯一性知,(x,y)过的解与过点(x1y)是同一条积 分曲线.即此解可表示为:y=p(x,七1,y1) 结束 上一贡返回下页<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 = 0 0 y x x y ( , , ) y x x y 1 1 0 0 =( , , ) 解关于初值的一些基本性质 解关于初值的对称性: 设(2.1)满足 y x y ( ) 0 0 = 的解是唯一的,记为 则在解的存在范围内,有 y x x y 0 0 =( , , ) 成立 . 1 事实上,在解的存在区间内任取一值 x ,且记 §3.3 解对初值的连续性和可微性 1 1 则由解的唯一性知, 过的解与过点 ( , ) x y 是同一条积 分曲线. 即此解可表示为: 0 0 ( , ) x y = 1 1 y x x y ( , , )
33解对初值的连续性和可微性 (y1) (xo2Yo) XI b 并且J=(xo,x1,1),由于(x1,y1)是在积分曲线上任意取的 一点,因此关系式'=(xo,x,)对该积分曲线上的任意点 都成立. 结束 帮助 返
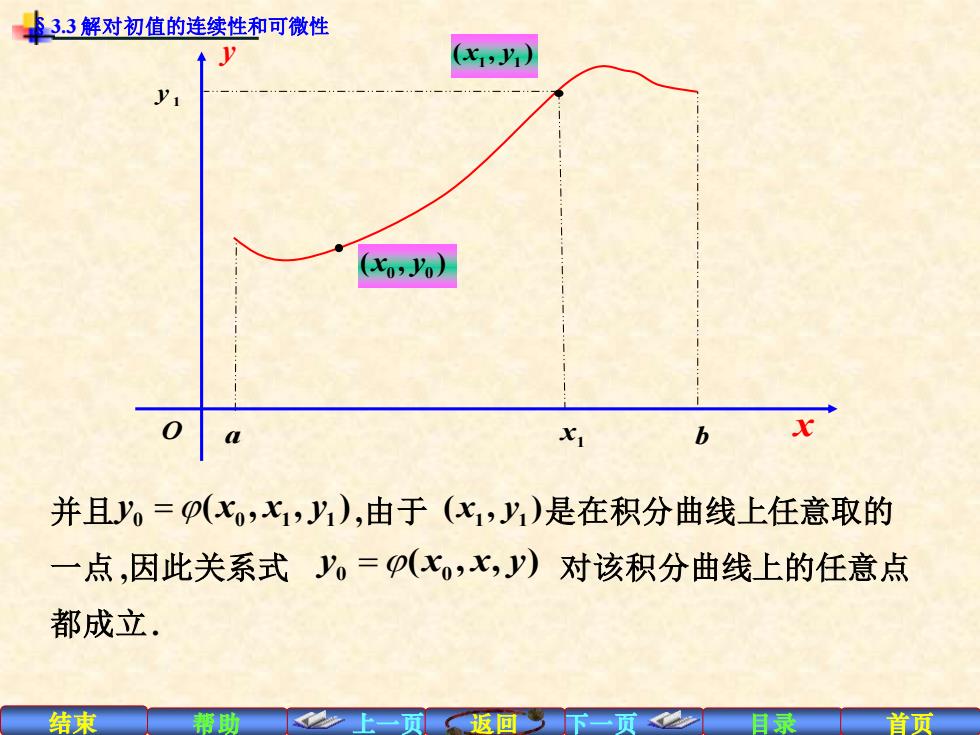
结束 帮助 上一页 返回 下一页 目录 首页 并且 ,由于 是在积分曲线上任意取的 一点 ,因此关系式 对该积分曲线上的任意点 都成立. y x x y 0 0 1 1 =( , , ) 1 1 ( , ) x y y x x y 0 0 =( , , ) 1 y 1 1 ( , ) x y O a x1 b 0 0 ( , ) x y y x §3.3 解对初值的连续性和可微性

33解对初值的连续性和可微性 引理.如果函数f(x,y在某域D内连续,且关于y满足 Lipschitzz条件(Lip常数为L),则对(2.1)的任意两个解p(x)及(r), 在它们公共存在的区间内成立着不等式 o(x)-(x)(x)-(x)ex 其中x为所考虑区间内的某一值。 证明:设p(x),(x)的公共存在区间为[a,b],令 V(x)=(p(x)-(x)),xEla,b] ◆V'(x)=2(p(x)-(x)(p'(x)-'(x) =2(p(x)-(x)(f(x,p(x)-f(x,p(x)) ≤2L(p(x)-(x)=2LV(x) →V'(x)-2LV(x)≤0,两边乘e-2Lx:V'(x)e2-2Le2V(x)≤0 d(V(x)e2) ≤0 dx 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 引理. 如果函数 在某域 内连续,且关于 满足 Lipschitz条件(Lip常数为L) ,则对(2.1)的任意两个解 及 , 在它们公共存在的区间内成立着不等式 f x y ( , ) D y ( ) x ( ) x 0 0 0 ( ) ( ) ( ) ( ) L x x x x x x e − − − = − ( ) 2 V x x x x a b ( ) ( ) ( ) , [ , ] = − − 2 ( ) ( ) ( , ( )) ( , ( )) ( x x f x x f x x )( ) 0 其中 x 为所考虑区间内的某一值。 证明:设 ( ) x , ( ) x 的公共存在区间为 [ , ] a b ,令 V x x x x x ( ) 2 ( ) ( ) ( ) ( ) = − − ( )( ) §3.3 解对初值的连续性和可微性 ( ) 2 − = 2 ( ) ( ) 2 ( ) L x x LV x − V x LV x ( ) 2 ( ) 0 −2Lx e − − − 2 2 ( ) 2 ( ) 0 Lx Lx ,两边乘 : V x e Le V x ( ) − 2 ( ) 0 Lx d V x e dx

33解对初值的连续性和可微性 因此,对x,∈[M,b]及x,≤x≤b,积分上式,只有x≥x 才仅有 (es x V(x)e-2|s≤0,→V()e2u-V(x)e2≤0, V(x)≤V(x)e2x-,x≤x≤b 对于M≤x≤xw令-x=t,记-x0=to,则(2.1)变为 =-f-t,y) (*) dx 由下0g和密是方程杰-fx,)的解,所以易=-及 y=(-)是(*)的解.因为 左端 d9-0-do-f(x,p(x)=-f((-4,0-0)=右端 dt dx 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 − 2 ( ) 0 Lx x x dV x e dx dx − 0 2 ( ) 0, Lx x V x e x − − − 0 2 2 0 ( ) ( ) 0, Lx Lx V x e V x e §3.3 解对初值的连续性和可微性 x a b 0 [ , ] x x b 0 0 因此,对 及 ,积分上式,只有 x x 才仅有 − 0 2( ) 0 0 ( ) ( ) , x x V x V x e x x b 0 axx − = x t − = 0 0 对于 ,令 ,记 x t ,则(2.1)变为 = − − ( , ) ( ) dy f t y dx ( )t ( )t = ( , ) dy f x y dx y t = − ( ) y t = − ( ) () 由于 和 都是方程 的解,所以易知 及 是 的解. 因为 ( ) ( ) − = = − = − = − − − = ( ) ( ) , ( ) , ( ) d t d x f x x f t t dt dx 左端 右端

33解对初值的连续性和可微性 对t。≤t≤-u,积分上式 a'(t)=2[p(-t)-(-t)]-p'(-t)+'(-t)川 =-2[p(-t)+(-tf(-t,p(-t)-f(-t,(-t)1 ≤2L[p(-t)+(-t)][-p(-t)+(-t)]≤2La(t) a'()e2u-2Le2a(0)s0,=da(e dt 20 令a(t)=[p(-t)-(-t),则 .a≤x≤xo →-x,≤-x≤-0 ∫da()e“≤0,a(t)≤at,)e-,in≤t≤-a→t,≤t≤-m) a(:-x=V(x)a(4o)=V(xo),a(-x)≤a(t,)e2(-+) .V(x)≤V(x)e2(,a≤x≤.对x,x∈[a,b],有 V(x)≤V(x)e2-l p(x)-(x)≤p(x)-(xe4- 结束 帮助 上一面返回下一页2 首页
结束 帮助 上一页 返回 下一页 目录 首页 = − − − 2 令 a t t t ( ) [ ( ) ( )] ,则 a t t t t t ( ) 2[ ( ) ( )][ ( ) ( )] = − − − − − + − = − − + − − − − − − 2[ ( ) ( )][ , ( ) , ( ) ] t t f t t f t t ( ) ( ) − + − − − + − 2 [ ( ) ( )][ ( ) ( )] L t t t t 2 ( ) La t − − − 2 2 a t e Le a t ( ) 2 ( ) 0 Lt Lt , − ( ( ) ) 0 Lt d a t e dt 0 0 0 ) axx x x a t t a − − − − §3.3 解对初值的连续性和可微性 对 t t a 0 − ,积分上式 − 0 ( ) 0, t Lt t da t e − − 0 ( ) 0 0 a t a t e t t a ( ) ( ) L t t , = − = = 0 0 a t V x a t V x ( ) ( ) ( ) ( ) t x , , − + − 0 2 ( ) 0 ( ) ( ) L x x a x a t e − 0 2 ( ) 0 0 V x V x e a x x ( ) ( ) L x x , , 对 x x a b , [ , ] 0 ,有 − 0 2 0 ( ) ( ) L x x V x V x e − − − 0 0 0 ( ) ( ) ( ) ( ) L x x x x x x e

重3.3解对初值的连续性和可微性 我们说f(x,y)在点(x,y)连续是指当(x,y)在点(xo,y)的变 化很小时,即在(x,y)的充分小邻域时,相应的函数值f(x,y) 的变化很小.即f(x,y)与f(x,y)的差别很小. 用数学语言来叙述的话,那就是V£>0,3δ>0 当(x-x)2+(-)2<6有f(x,y)-f(x-y)<6 对于(2.1)的解y=p(x,xo,Jyo,)如果初值的变化很 小时,相应的解的变化也很小,那么解关于xo,'o就连续 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 0 0 f x y f x y ( , ) ( , ) 与 0 0 ( , ) x y ( , ) x y 0 0 ( , ) x y f x y ( , ) f x y ( , ) 0 0 我们说 在点 连续是指当 在点 ( , ) x y 的变 化很小时,即在 的充分小邻域时,相应的函数值 的变化很小. 即 的差别很小. 2 2 2 0 0 ( ) ( ) x x y y − + − 0, 0 0 0 f x y f x y ( , ) ( ) − − 用数学语言来叙述的话,那就是 当 , 有 = 0 0 y x x y ( , , ) 0 0 x y, 对于(2.1)的解 ,如果初值的变化很 小时,相应的解的变化也很小,那么解关于 就连续. §3.3 解对初值的连续性和可微性

33解对初值的连续性和可微性 解对初值的连续依赖定理 设f(x,y)于域G内连续且关于y满足局部的Lipschitzz条件, (,y)∈了y=p(x,xo,Jy是方程(2.1)满足初始条件y(x)=y 的解,定义于a,b],x∈[,b1那么,对于VE>0,3δ=δ(E,b) 使得当 (-x)2+(-y6)≤82 时,方程(2.1)的满足条件y()=的解y=p(x,xo,0) 在区间[4,b止也有定义,并且 p(x,xo,o)-(x,xo,o)& a≤x≤b 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 解对初值的连续依赖定理 设 于域 内连续且关于y 满足局部的Lipschitz条件, , 是方程(2.1)满足初始条件 的解,定义于 , 那么,对于 使得当 f x y ( , ) G ( , ) x y G 0 0 = 0 0 y x x y ( , , ) y x y ( ) 0 0 = [ , ] a b x a b 0 [ , ] = 0, ( , , ) a b 2 2 2 0 0 0 0 ( ) ( ) x x y y − + − ( , , ) ( , , ) x x y x x y a x b 0 0 0 0 − y x y ( ) 0 0 = = 0 0 y x x y ( , , ) [ , ] a b 时,方程(2.1)的满足条件 的解 在区间 上也有定义,并且 §3.3 解对初值的连续性和可微性
3.3解对初值的连续性和可微性 要说明两点:1解p(x,)至少在区间[,b上有定义. 2 要说明,当值变化很小时,相应的解的 变化也很小. 0(x,0】 P(x,xo2Vo) a b 结束 帮助 返回 首页
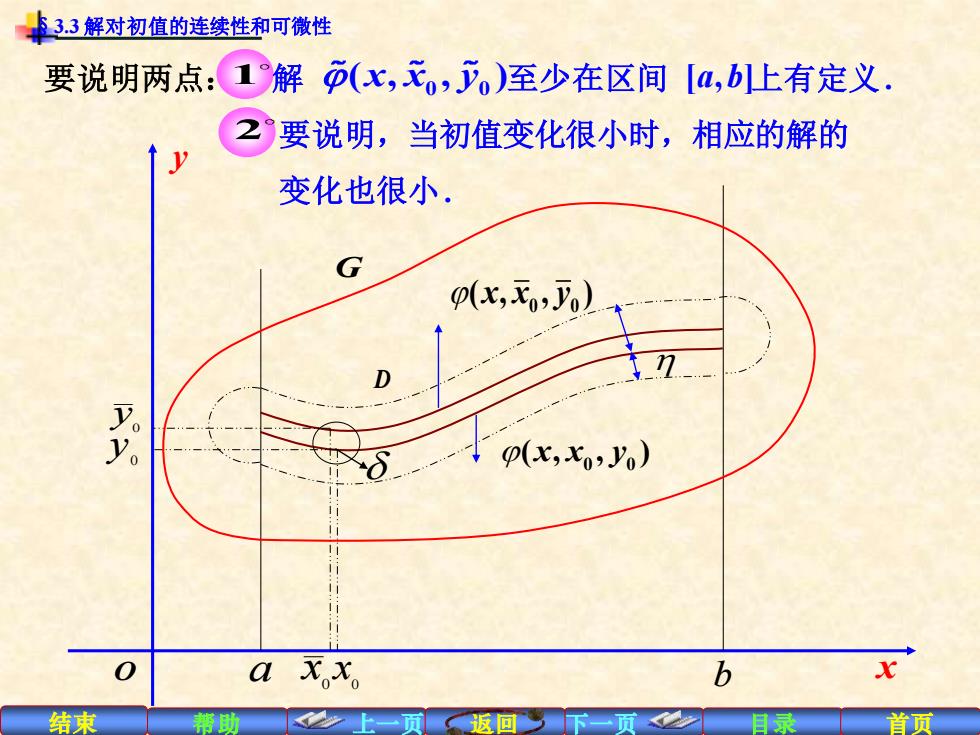
结束 帮助 上一页 返回 下一页 目录 首页 要说明两点: 解 至少在区间 上有定义. 要说明,当初值变化很小时,相应的解的 变化也很小. 1 0 0 ( , , ) x x y [ , ] a b 2 x y 0 0 ( , , ) x x y 0 0 y 0 ( , , ) x x y 0 x 0 a x b y0 O D G §3.3 解对初值的连续性和可微性