
§2.解的延拓 讲授内容:解的延拓概念,解的延拓定理 讲授要点:解的延拓概念 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 §2. 解的延拓 讲授内容: 解的延拓概念 , 解的延拓定理 讲授要点: 解的延拓概念

32解的延拓 y'=f(x,y) (2.1) y(xo)=yo 定理1是局部性的,因为根据这条定理,(2.1)的解存 在不成问题,但解的存在区间为x-x≤h,其中∈C(G), h由函数f(x,y)在点(x,)附近的局部性质所决定, b 事实上h=min(a, M=max f(x,y) (x,y)ER 而R:x-x≤a,y-y≤b是包含在G中的一个闭区域.显 然M越大,h越小.因此,不论区域G多么大,定理1所能肯定的 也只是包含x,的某一可能很小的区间上有解在. 结束 助上一返回下一页<2■目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 ( ) = 0 0 = ( , ) 2.1 ( ) y f x y y x y 定理1 是局部性的,因为根据这条定理, (2.1)的解存 在不成问题,但解的存在区间为 , 其中 h 由函数 在点 附近的局部性质所决定. − 0 x x h f C G ( ). f x y ( , ) 0 0 ( , ) x y 事实上 = min( , ) b h a M = ( , ) max ( , ) x y R M f x y §3.2 解的延拓 − − 0 0 R x x a y y b : , G M h 而 是包含在 中的一个闭区域 .显 然 越大, 越小. 因此 , 不论区域 多么大, 定理1所能肯定的 也只是包含 的某一可能很小的区间上有解在. G 0 x

32解的延拓 y'= -1 例:考虑 (1) 满足y(0)=0的解. 2 右端函数在整个平面上有定义,连续.考虑区间 R:x-0≤2,y-0≤2 之-ys2ng川房h=mia安月 b 2 a (x.Y)ER 所以,对于(定理1所肯定的解的存在区间为[当y≠士1时, 方程的通解为 +ce' y=- -ce .1-ex 由y0)=0,得c=-1.所以(1) 满足0)=0的解为y=1+e 此解的定义区间为(-∞,+∞),X→+0时,y→1,当x→-o0时, y→-1 那么,我们自然就要问,能否将解的存在区间加以扩大? 若能扩大,则能扩大到什么程度 结束☐ 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 − = 2 1 (1) 2 y 例: 考虑 y 右端函数在整个 xy 平面上有定义,连续.考虑区间 = = = = ( , ) 3 4 max ( , ) , min( , ) x y R 2 3 b M f x y h a M R x y : 0 2, 0 2 − − − = = 2 1 ( , ) , 2 2 y f f x y y y 满足 y(0) 0 = 的解 . §3.2 解的延拓 所以,对于(1) 定理1 所肯定的解的存在区间为 .当 时, 方程的通解为 − 4 4 , 3 3 y 1 + = − 1 1 x x ce y ce 由 y(0) 0 = ,得 c = −1 . 所以 (1) 满足 y(0) 0 = 的解为 − = + 1 . 1 x x e y e ( , ) − + x → + y →1, y → −1 此解的定义区间为 , 时, 当 x → − 时, 那么,我们自然就要问,能否将解的存在区间加以扩大? 若能扩大,则能扩大到什么程度

32解的延拓 设(2.1)右端函数(x,y)在某一区域G内连续,且关 于y满足局部的Lipschitzz条件. 结束 精助州上一贡下一页<2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 设(2.1)右端函数 f x y ( , ) 在某一区域 G 内连续,且关 于 满足局部的Lipschitz条件 . y §3.2 解的延拓

3.2解的延拓 最后我们得到一个解y=0(x),它已经不能再向左右方延拓了, 这样的解成为(21)的饱和解,确切定义为: 定义:设p(x为(2.1)的定义在(a,B)上的解,若存在 (2.1)的另一解(x),它的定义区间为a,),并且 () (a,B)p(a,B)但(a,B)≠(a,B) (2) p(x)=p(x), 当x∈(a,)时 则我们说p(t)是可延展的,并称(x)是p(x)在(a,)上的一个 延展.相反,如果不存在满足上述条件的解p(x)则称p(x),x∈(@,B) 是(2.1)的一个饱和解. 若f(x,y)∈C(G),p(x)是2.1)的一个解,定义区间为(C,B), 则p(a+0),p(B-0必存在有限,并当(a,p(a+0)∈G(B,p(B-0)∈G) 时,解p(t)尚可从向左(从B向右)延展. 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 最后我们得到一个解 , 它已经不能再向左右方延拓了, 这样的解成为(2.1)的饱和解,确切定义为: y x =( ) ( ) x ( , ) ( ) x ( , ) 定义:设 为(2.1)的定义在 上的解,若存在 (2.1)的另一解 ,它的定义区间为 ,并且 (1) ( , ) ( , ) ( 但 , ) , ) ( (2) ( ( ) x x ) , 当 x ( , ) 时 §3.2 解的延拓 ( ) x x ( , ) ( ) x ( ) x ( , ) ( ) x 则我们说 ( )t 是可延展的,并称 是 在 上的一个 延展 . 相反,如果不存在满足上述条件的解 则称 , 是(2.1)的一个饱和解. ( )t 若 , 是(2.1)的一个解, 定义区间为 , 则 必存在有限,并当 时,解 尚可从 向左(从 向右)延展. f x y C G ( , ) ( ) ( , ) ( 0), ( 0) + − ( ) x ( , ( 0) ( , ( 0)) + − ) G G ( )

32解的延拓 任一饱和解y=(x)最大存在区间必定是开区间(,B), 因为如果这个区间右端是闭的,那么B便是有限数,且(B,(B)∈G 根据上面讲的,解y=(x)还可向右延展。从而它是非饱和解 现问,一个解y=p(x)向左右两方延拓的最终情况如何 解的延展理: 如果方程(3.1)右端的函数f(x在有界区域中连续,且在 G 内关于满足局部利普希茨条件,那么方程(3.1)的通过心:何一 点(飞,的解y可延拓,直到点 任意接近区域 的边界.以向增大的一方的延拓来说,如果y=风能诞延拓到 区间x,≤x≤地则当 时,→m 趋氏函域)的边界.G 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 任一饱和解 最大存在区间必定是开区间 . y x = ( ) ( , ) ( , ( )) G y x = ( ) 因为如果这个区间右端是闭的,那么 便是有限数, 且 ,根据上面讲的,解 还可向右延展。从而它是非饱和解. ( , ( )) x x 如果方程(3.1)右端的函数 在有界区域 中连续,且在 内关于 满足局部利普希茨条件,那么方程(3.1)的通过 内任何一 点 的解 可以延拓 , 直到点 任意接近区域 的边界.以向 增大的一方的延拓来说,如果 只能延拓到 区间 上,则当 时, 趋于区域 的边界. f x y ( , ) G y ( , ) x y 0 0 G y x = ( ) G x y x = ( ) x x m 0 x m → ( , ( )) x x G G 解的延展理: §3.2 解的延拓 现问,一个解 y x = ( ) 向左右两方延拓的最终情况如何

32解的延拓 推论2.若是无界区域,则它可能有境界线(如半平面)也可 能没有境界线(例如全平面),所以有两种可能(以增大方向来说): 1 y=o(x) x∈[xo,+o) 2°y=p(x) x∈[x,m),m为有限,则 limg(x)=o lim p(x,(x)),G)=0 x->m 例1.讨论y=广1分别通过0.0和(1n2,-3的解的存在区间 解:过(0,0)的解的存在区间为(一∞,+∞) 过2,3》的解为)y甚仁存作送间为一即向左只可廷拓动 此例说明,f(x,y)的定义区间即便是无界(无境界)的区域, 解y=p(x)的最大存在区间也不一定是(一o∞,+o), 结束 帮助 返回
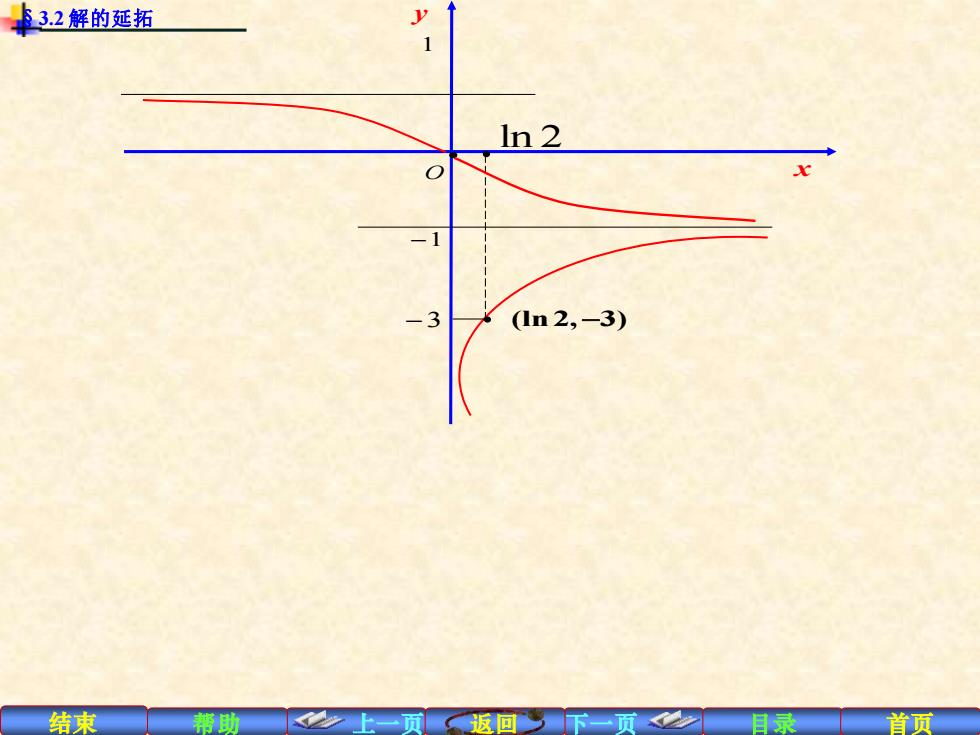
结束 帮助 上一页 返回 下一页 目录 首页 推论2. 若 是无界区域 , 则它可能有境界线(如半平面)也可 能没有境界线 (例如全平面) , 所以有两种可能(以 增大方向来说): G x = + 0 1 ( ) [ , ) y x x x = 0 2 ( ) [ , ) , y x x x m m为有限, 则 2 1 2 y y − 例1.讨论 = 分别通过 (0 0 ln2, 3) ,)和( − 的解的存在区间. 解:过 (0,0) 的解的存在区间为 ( , ) − + §3.2 解的延拓 → → lim ( ) lim ( , ( )), 0 x m x m x x x G = = 或 过 (ln 2, 3) − 的解为 + = − 1 , (0, ), 0 1 存在区间为 即向左只可延拓到 x x e y e 此例说明, 的定义区间即便是无界(无境界) 的区域, 解 的最大存在区间也不一定是 . f x y ( , ) y x = ( ) ( , ) − +
3.2解的延拓 In2 -3 n2,-3) 结束 助上一贡返回下一页<目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 §3.2 解的延拓 y x ln 2 O −3 (ln 2, 3) − −1 1

Dy=.1)2的解 5 过(0,0)的解 过0dn2.3)的解 1 Y轴 0 In2 0 -1 -1 -3 3 0n2,3) -4 5 -4 3 -2 -1 0 2 3 4 X轴 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页

32解的延拓 例2. =1+Inx d Jy(1)=0 解:∫(x,y在右半平面满足解的存在唯一性定理及延展定 理的条件.区域G为无界区域,它满足y1)=0解为y=xnx. 解的定义域为(0,+o),且当x>0时,y使xnx→0 说明imp[x,p(x),∂G]=0 lim Inx =0 x01 lim x→0 1 x 对于例2, 画出它的图形。由y'=1+lnx=0→x=e 0所以,(e,-e为极小值点. 在e内y>0y弹调增y0辈 在(0,e1)内y'0,曲线上凸. 结束 帮助上一贡返回下页< 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 例2. 1 ln (1) 0 dy x y dx = + = 解: 在右半平面满足解的存在唯一性定理及延展定 理的条件.区域 为无界区域,它满足 解为 . f x y ( , ) G y(1) 0 = y x x = ln 解的定义域为 (0, ) + ,且当 x →0 时, y 使 x x ln 0 → . 说明 lim [( , ( ), ] 0 x m x x G → = §3.2 解的延拓 0 0 2 1 ln lim lim 0 x x 1 1 x x x x → → = = − 对于例2,画出它的图形。 1 y x x e 1 ln 0 − 由 = + = = − = = = 1 1 0 x e y e x − − − 1 1 所以, ( , ) e e 为极小值点. − + 1 在 ( , ) e 内 y 0 , y 单调增加, y 0 曲线 上凸 . −1 在(0, ) e 内y 0 , y 单调减少, , y 0 曲线上凸