
新疆大学 《概率论与数理统计》课程教学大纲 英文名称:Probability and Statistics 课程编号:A05006B105202B105303B056102B105002 课程类型:必修、基础理论课 总学时:64学时 学分:3.5学分 适用对象:理科大面积 先修课程:高等数学、线性代数 使用教材及参考书: 教材:《概率论与数理统计》,王明慈,沈恒范编,高等教育出版社 参考书:《概率论与数理统计》,刘婉茹编,高等教育出版社 《概率论与数理统计》,盛骤,潘承毅编,高等教育出版社 课程性质、目的和任务 本课程是理工科学生的一门基础理论课。概率统计是研究随机现象客观规律性的一门学科,随着科 学技术的发展以及人们对随机现象规律性认识的需要,概率随机现象规律性认识的需要,概率统计 的思想方法正日益渗透到自然科学和社会科学的众多领域中。通过本课程的学习,使学生掌握概率 统计的基本概念,了解它的基本理论和方法,从而使学生初步掌握处理随机现象的基本思想和方 法,培养学生运用概率统计分析和解决实际问题的能力。 二、教学基本要求 要求学生理解并掌握随机事件与概率的计算,理解并掌握随机变量及概率分布的性质,掌握随机 变量的数字特征,了解大数定律,会用中心极限定理求近似概率,了解树拉统计的基本概念,掌握 参数估计及假设检验的基本理论和方法,并会用这些方法解决一些实际问题。 三、 教学内容及要求 第一章随机事件及其概率: 1、样本空间随机事件2、概率的定义及性质3、古典概型:4条件概率概率的乘法公式。 5.随机事件的独立性;6.伯努利概型 教学要求: 1.了解样本空间的概念,理解随机事件的概念,掌握事件的关系与运算。 2. 理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率,掌握概率的加法公 式、乘法公式、全概率公式。 3.理解事件的独立性的概念,掌握用事件的独立性进行概率计算;理解独立重复试验的概念,掌握 计笪有关事件鼾率的方法 第二章随机变量及其分布 1、随机变量的概念,2.离散随机变量;3超几何分布,二项分布,泊松分布:4.连续型随机变量;5. 均匀分布,指数分布;6.随机变量的分布函数:7.多维随机变量及其分布;8.随机变量的独立性:9.随机 变量函数的分布! 教学要求: 1.理解随机变量及其概率分布的概念;理解离散型随机变量及其概率分布的概念,掌握二项分布 超几何分布、泊松poisson)分布及其应用。 2.理解连续型随机变量及其概率密度的概念,掌握均匀分布、指数分布及其应用
新 疆 大 学 《概率论与数理统计》课程教学大纲 英文名称:Probability and Statistics 课程编号:A05006 B105202 B105303 B056102 B105002 课程类型:必修、基础理论课 总学时:64学时 学 分:3.5学分 适用对象:理科大面积 先修课程:高等数学、线性代数 使用教材及参考书: 教材:《概率论与数理统计》,王明慈,沈恒范编,高等教育出版社 参考书:《概率论与数理统计》,刘婉茹编,高等教育出版社 《概率论与数理统计》,盛骤,潘承毅编,高等教育出版社 一、 课程性质、目的和任务 本课程是理工科学生的一门基础理论课。概率统计是研究随机现象客观规律性的一门学科,随着科 学技术的发展以及人们对随机现象规律性认识的需要,概率随机现象规律性认识的需要,概率统计 的思想方法正日益渗透到自然科学和社会科学的众多领域中。通过本课程的学习,使学生掌握概率 统计的基本概念,了解它的基本理论和方法,从而使学生初步掌握处理随机现象的基本思想和方 法,培养学生运用概率统计分析和解决实际问题的能力。 二、教学基本要求 要求学生理解并掌握随机事件与概率的计算,理解并掌握随机变量及概率分布的性质,掌握随机 变量的数字特征,了解大数定律,会用中心极限定理求近似概率,了解树立统计的基本概念,掌握 参数估计及假设检验的基本理论和方法,并会用这些方法解决一些实际问题。 三、 教学内容及要求 第一章 随机事件及其概率: 1、样本空间随机事件; 2、概率的定义及性质 3、古典概型; 4.条件概率概率的乘法公式。 5.随机事件的独立性; 6.伯努利概型 教学要求: 1. 了解样本空间的概念,理解随机事件的概念,掌握事件的关系与运算。 2. 理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率,掌握概率的加法公 式、乘法公式、全概率公式。 3.理解事件的独立性的概念,掌握用事件的独立性进行概率计算;理解独立重复试验的概念,掌握 计算有关事件概率的方法 第二章随机变量及其分布 1、 随机变量的概念; 2. 离散随机变量; 3.超几何分布,二项分布,泊松分布; 4.连续型随机变量; 5. 均匀分布,指数分布; 6.随机变量的分布函数; 7.多维随机变量及其分布; 8.随机变量的独立性; 9.随机 变量函数的分布. 教学要求: 1. 理解随机变量及其概率分布的概念;理解离散型随机变量及其概率分布的概念,掌握二项分布、 超几何分布、泊松(poisson)分布及其应用。 2. 理解连续型随机变量及其概率密度的概念,掌握均匀分布、指数分布及其应用

3.理解分布函数的概念及性质:会计算与随机变量相联系的事件的概率。 4. 理解二维随机变量的概念,理解二维随机变量的联合分布的概念、性质及两种基本形式:离散 型联合概率分布、边缘分布;连续型联合概率密度、边缘密度;会利用二维概率分布求有关事件的 概率。 5.理解随机变量的独立性和不相关概念,掌握离散型和连续型随机变量独立的条件 6.会根据自变量的概率分布求其简单函数的概率分布。 第三章随机变量的数字特征 1、数学期望2、方差3、矩4、协方差与相关系数:5切比雪夫不等式与大数定理 教学要求: 1.理解随机变量的数字特征(数学期望、方差、标准差、矩、协方差、相关系数)的概念,并会运 用数字特征的基本性质计算具体分布的数字特征,掌握常用分布的数字特征。 2.根据随机变量的概率分布求其函数的数学期望*;会根据二维随机变量的概率分布求其函数的数学 期 3.了解切比雪夫不等式;了解切比雪夫大数定律、伯努利大数定律。 第四章正态分布 1、正态分布的概率密度与分布函数2、正态分布的数字特征:3.正态分布的线性性质4、二维正态分 布5、中心极限定理 教学要求: 1、了解正态分布的概率密度与分布函数,掌握其数字特征及其线性性质。 2、了解二维正态分布的概率密度,理解其中参数的概率意义。 3、了解棣莫弗-拉普拉斯定理和列维林德伯格定理 第五章数理统计的基本知识 1、总体与样本 2、样本分布函数直方图,样本函数与统计量,分布,分布,F分布 3、正态总体统计量的分布 教学要求: 1. 理解总体、样本、简单随机样本、样本分布函数、统计量、样本均值、样本方差和样本矩的概 2.了解分布,分布,F分布的概念及性质。 3。了解下态总体的统计量的分布. 第六章参数估计 1、参数的点估计,判别估计量好坏的标准,正态总体参数的区间估计 2、两个正态总体均值差与方差比的区间估计 3、非正态总体的区间估计举例,单侧置信限 教学要求: 1. 理解参数的点估计、估计量与估计值的概念,掌握矩估计法和最大似然估计法 2.了解估计量的无偏性、有效性和一致性的概念,并会验证估计量的无偏性。 3. 了解区间估计的概念,会求单个正态总体的均值和方差的置信区间,会求两个正态总体的均值差 和方差比的置信区间。 第七章假设检验 1、假设检验的基本概念,2、单个正态总体参数的假设检验,3、两个正态总体参数的假设检验, 4、非正态总体参数的假设检验举例,5、正态总体的拟合检验 四、重点和难点(所列内容为重点,难点用*表示)
3. 理解分布函数的概念及性质;会计算与随机变量相联系的事件的概率。 4. 理解二维随机变量的概念,理解二维随机变量的联合分布的概念、性质及两种基本形式:离散 型联合概率分布、边缘分布;连续型联合概率密度、边缘密度;会利用二维概率分布求有关事件的 概率。 5. 理解随机变量的独立性和不相关概念,掌握离散型和连续型随机变量独立的条件。 6. 会根据自变量的概率分布求其简单函数的概率分布。 第三章随机变量的数字特征 1、 数学期望2、方差 3、矩 4、协方差与相关系数;5.切比雪夫不等式与大数定理. 教学要求: 1. 理解随机变量的数字特征(数学期望、方差、标准差、矩、协方差、相关系数)的概念,并会运 用数字特征的基本性质计算具体分布的数字特征,掌握常用分布的数字特征。 2. 根据随机变量的概率分布求其函数的数学期望*;会根据二维随机变量的概率分布求其函数的数学 期望* 3. 了解切比雪夫不等式;了解切比雪夫大数定律、伯努利大数定律。 第四章正态分布 1、 正态分布的概率密度与分布函数2、正态分布的数字特征; 3.正态分布的线性性质 4、二维正态分 布 5、中心极限定理 教学要求; 1、了解正态分布的概率密度与分布函数,掌握其数字特征及其线性性质。 2、了解二维正态分布的概率密度,理解其中参数的概率意义。 3、了解棣莫弗-拉普拉斯定理和列维-林德伯格定理。 第五章数理统计的基本知识 1、 总体与样本 2、 样本分布函数 直方图,样本函数与统计量,分布,t分布,F分布 3、 正态总体统计量的分布 教学要求: 1. 理解总体、样本、简单随机样本、样本分布函数、统计量、样本均值、样本方差和样本矩的概 念。 2. 了解分布, t分布, F分布的概念及性质。 3. 了解正态总体的统计量的分布。 第六章参数估计 1、 参数的点估计,判别估计量好坏的标准,正态总体参数的区间估计 2、 两个正态总体均值差与方差比的区间估计 3、 非正态总体的区间估计举例,单侧置信限 教学要求: 1. 理解参数的点估计、估计量与估计值的概念,掌握矩估计法和最大似然估计法。 2. 了解估计量的无偏性、有效性和一致性的概念,并会验证估计量的无偏性。 3. 了解区间估计的概念,会求单个正态总体的均值和方差的置信区间,会求两个正态总体的均值差 和方差比的置信区间。 第七章 假设检验 1、假设检验的基本概念,2、单个正态总体参数的假设检验,3、两个正态总体参数的假设检验, 4、非正态总体参数的假设检验举例,5、正态总体的拟合检验 四、重点和难点(所列内容为重点,难点用*表示)
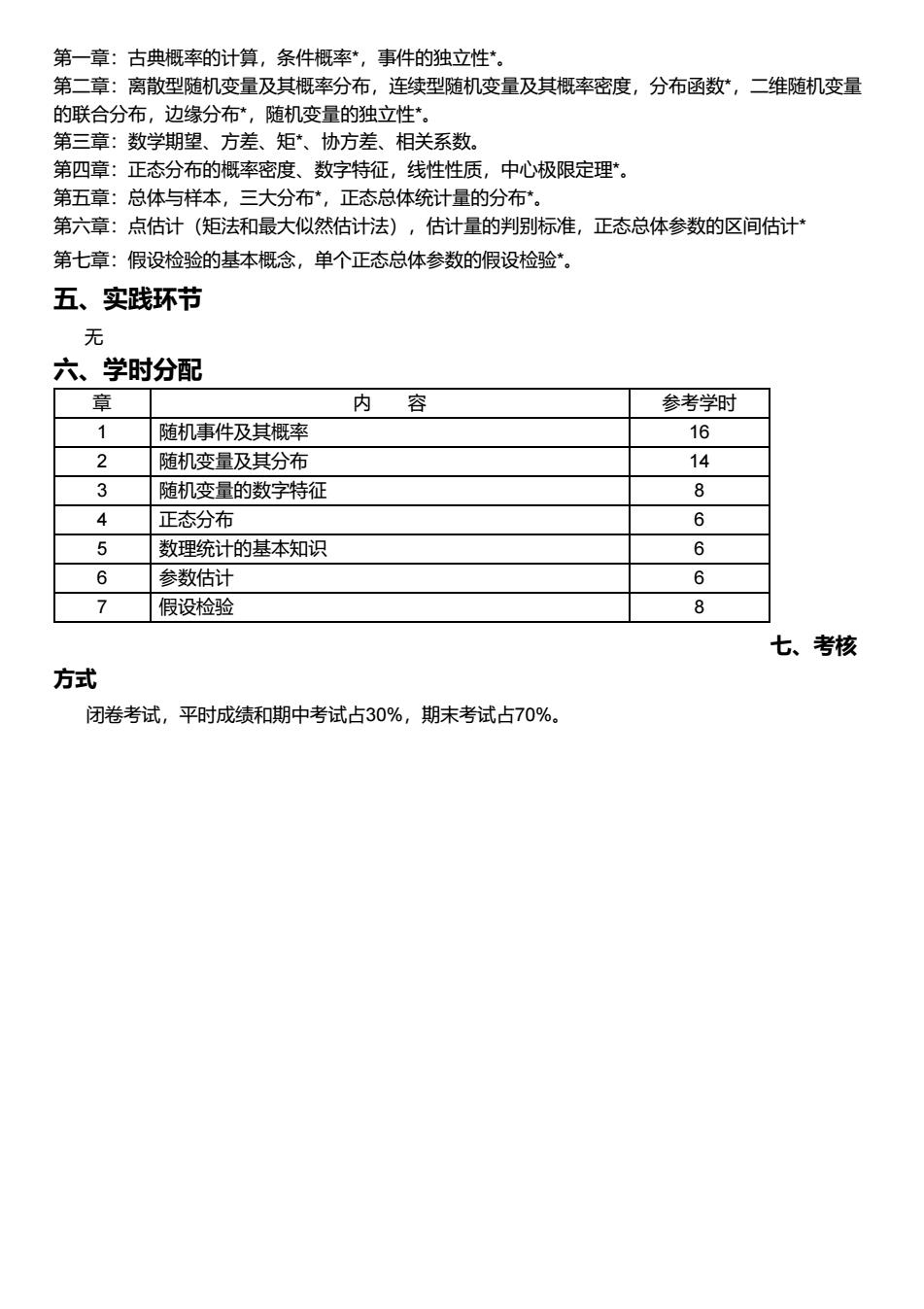
第一章:古典概率的计算,条件概率*,事件的独立性*。 第二章:离散型随机变量及其概率分布,连续型随机变量及其概率密度,分布函数*,二维随机变量 的联合分布,边缘分布*,随机变量的独立性*。 第三章:数学期望、方差、矩*、协方差、相关系数。 第四章:正态分布的概率密度、数字特征,线性性质,中心极限定理*。 第五章:总体与样本,三大分布*,正态总体统计量的分布*。 第六章:点估计(矩法和最大似然估计法),估计量的判别标准,正态总体参数的区间估计* 第七章:假设检验的基本概念,单个正态总体参数的假设检验*。 五、实践环节 无 六、学时分配 章 内 容 参考学时 1 随机事件及其概率 16 2 随机变量及其分布 14 3 随机变量的数字特征 ⊙ 4 正态分布 6 5 数理统计的基本知识 6 6 参数估计 6 7 假设检验 8 七、考核 方式 闭卷考试,平时成绩和期中考试占30%,期末考试占70%
章 内 容 参考学时 1 随机事件及其概率 16 2 随机变量及其分布 14 3 随机变量的数字特征 8 4 正态分布 6 5 数理统计的基本知识 6 6 参数估计 6 7 假设检验 8 第一章:古典概率的计算,条件概率*,事件的独立性*。 第二章:离散型随机变量及其概率分布,连续型随机变量及其概率密度,分布函数*,二维随机变量 的联合分布,边缘分布*,随机变量的独立性*。 第三章:数学期望、方差、矩*、协方差、相关系数。 第四章:正态分布的概率密度、数字特征,线性性质,中心极限定理*。 第五章:总体与样本,三大分布*,正态总体统计量的分布*。 第六章:点估计(矩法和最大似然估计法),估计量的判别标准,正态总体参数的区间估计* 第七章:假设检验的基本概念,单个正态总体参数的假设检验*。 五、实践环节 无 六、学时分配 七、考核 方式 闭卷考试,平时成绩和期中考试占30%,期末考试占70%