
综龄习题三

1.甲、乙两台机器一天中出现次品的概率分布分别为: p(x) 0.4 0.3 0.2 p(y) 0.3 0.5 0.2 若两台机器的日产量相同,问哪台机器较好? 解:EX)=0×0.4+1×0.3+2×0.2+3×0.1=1; EY0=0×0.3+1×0.5+2×0.2+3×0=0.9 从上式可知乙机器较好
1.甲、乙两台机器一天中出现次品的概率分布分别为: 若两台机器的日产量相同,问哪台机器较好? 解:E(X)=0×0.4+1×0.3+2×0.2+3×0.1=1; E(Y)=0×0.3+1×0.5+2×0.2+3×0=0.9 从上式可知乙机器较好。 X 0 1 2 3 p(x) 0.4 0.3 0.2 0.1 Y 0 1 2 3 p(y) 0.3 0.5 0.2 0

2.某种电子元件的寿命X(单位:h)的概率密度为: f(x)= a"xe@,x>0 0, x≤0 其中 α>0为常数。求这种电子元件的平均寿命。 解:E(X)=a2xe“k t=as"Pe =T(3)/a=2/a. 网国☒
( )/ / . ( ) 3 2 1 0 2 0 2 2 = = = = + − + − t x t e dt E X x e dx t x 2.某种电子元件的寿命X(单位:h)的概率密度为: 其中 为常数。求这种电子元件的平均寿命。 . , x xe , x f ( x ) x = − 0 0 0 2 0 解:

3.设随机变量X的概率密度为: f(x)= x“,0<x<1 0, 其它 已知EX)=0.75,求k及C的值。 解:由题意, f()d=fkx"d-1 E(X)=xk=0.75 k=a+1 a=2 →
3.设随机变量X的概率密度为: 已知E(X)=0.75,求k及 的值。 . . ( ) ( ) . ( ) = = = + = + = = = = + − 3 2 0 75 2 1 0 75 1 1 0 1 0 k k k E X x kx dx f x dx kx dx 解:由题意, . , , ( ) = 0 其 它 kx 0 x 1 f x

4.设随机变量X的概率分布如下: 2 Px(xi 1/6 1/6 1/6 1/2 求E(X),E(-2X+1),E(X2) 解:E()=(-x。+0x1×。*2×2 E(-2X+1)=3× 6 E0X9)-1x0x
4.设随机变量X的概率分布如下: 求 ( ); ( 2 1); ( ). 2 E X E − X + E X 1/6 1/6 1/6 1/2 X -1 0 1 2 ( ) X i p x ( ) . ( ) ( ) ( ) ; ( ) ( ) ; 3 1 2 2 1 4 6 1 1 6 1 0 6 1 1 1 2 1 3 6 1 1 6 1 1 6 1 2 1 3 1 2 1 2 6 1 1 6 1 0 6 1 1 2 = + + + = − + = + + − + − = − = − + + + = E X E X 解: E X
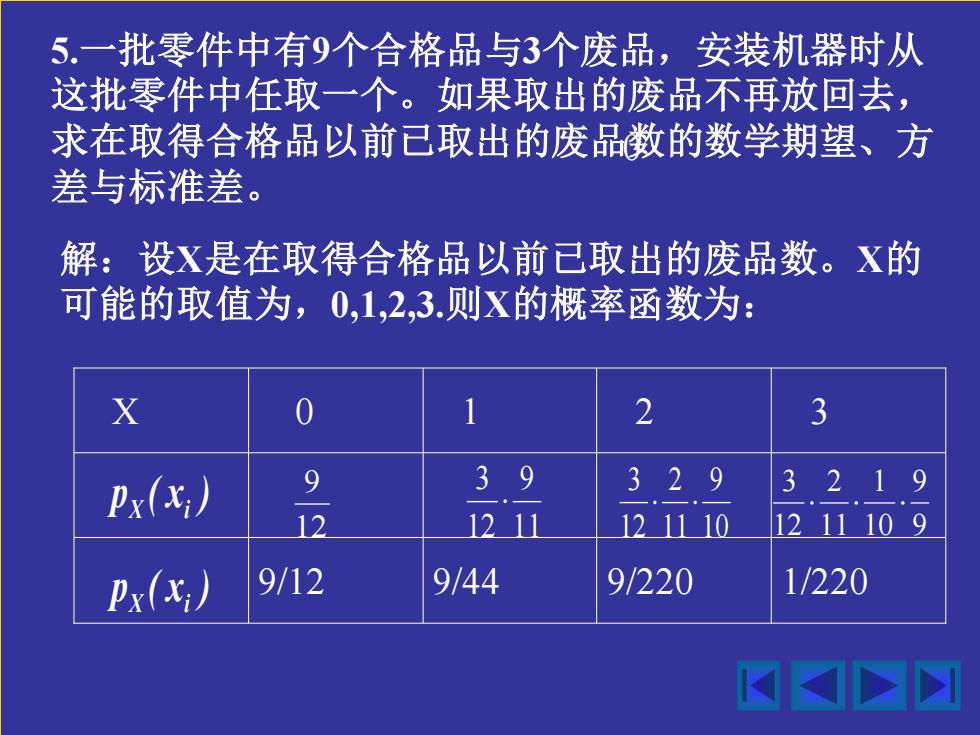
5.一批零件中有9个合格品与3个废品,安装机器时从 这批零件中任取一个。如果取出的废品不再放回去, 求在取得合格品以前已取出的废品数的数学期望、方 差与标准差。 解:设X是在取得合格品以前已取出的废品数。X的 可能的取值为,0,1,2,3.则X的概率函数为: X 0 1 2 3 Px(x;) 9 39 329 321 12 1211 121110 1211109 Px(xi) 9/12 9144 9/220 1/220
5.一批零件中有9个合格品与3个废品,安装机器时从 这批零件中任取一个。如果取出的废品不再放回去, 求在取得合格品以前已取出的废品数的数学期望、方 差与标准差。 解:设X是在取得合格品以前已取出的废品数。X的 可能的取值为,0,1,2,3.则X的概率函数为: 0 9/12 9/44 9/220 1/220 X 0 1 2 3 p ( x ) X i p ( x ) X i 12 9 11 9 12 3 10 9 11 2 12 3 9 9 10 1 11 2 12 3

X 0 1 2 3 Px(x;) 9 39 329 3219 12 1211 121110 1211109 Px(x;) 9/12 9/44 9/220 1/220 E(X)=0x3+1x 9 9 1 +2× +3× 0.3; 4 44 220 220 E(X2)=0x3+1× 9 1 +4× +9× =0.4; 44 220 220 D(X)=E(X2)-IE(X)12=0.31
( ) ( ) [ ( )] . . ( ) . ; ( ) . ; 0 31 0 4 220 1 9 220 9 4 44 9 1 4 3 0 0 3 220 1 3 220 9 2 44 9 1 4 3 0 2 2 2 = − = = + + + = = + + + = D X E X E X E X E X 9/12 9/44 9/220 1/220 X 0 1 2 3 p ( x ) X i p ( x ) X i 12 9 11 9 12 3 10 9 11 2 12 3 9 9 10 1 11 2 12 3

6.设随机变量X的分布函数为: [0, x1 试确定常数a,b,并求EX)、DX)。 解:由已知随机变量X的分布函数的其概率密度: 仁e海-产=am比=b1 F0)=a+sin1=a+ 1π =a+二=1,(连续性) π2 2
= + = + = + = = = = − = + − − − ( ) arcsin ,( ) ( ) arcsin | 1 连续性 2 1 2 1 1 1 1 1 1 1 1 1 1 2 F a a a dx b x b x b f x dx 6.设随机变量X的分布函数为: 试确定常数a,b,并求E(X)、D(X)。 . , arcsin , , ( ) + − − = 1 1 1 1 0 1 x a b x x x F x 解:由已知随机变量X的分布函数的其概率密度:

ek='=n咖北== F0=1=+号+ 2=0+2,(连续倒 Ew-n=R-aF=z D(X)=EX2)-IE(X)=1/2. 网国☒
( ) ( ) [ ( )] / . ( ) ; ( ) / ; . ( ) arcsin ,( ) ( ) arcsin | 1 2 1 2 1 0 1 2 1 1 1 2 1 2 1 1 1 1 1 1 2 2 1 1 2 2 2 1 1 2 1 1 1 1 2 = − = = − = = − = = = = + = + = + = = = = − = − − + − − − D X E X E X dx x x dx E X x x E X a b F a a a dx b x b x b f x dx 连续性

7.设随机变量X服从自由度为k的分布,其概率密度 为: f(x)=22Tk/2 x2-ex2,x>0; 0, x≤0. 其中k为正整数,求X的数学期望和方差。 解: W-ksg E2-7h”gnv 2Tk12+1=k5 T(k/2)
( / ) ; ( / ) ( / ) / ( / ) ( / ) ( ) ( / ) ( / ) / / / / / / / k k k t e dt k t x x e dx k x e dx k E X k k t k k x k k x k = + = = = = + + + − − + + − − 2 1 2 2 2 2 2 1 2 2 2 1 2 2 1 0 2 1 2 1 1 2 0 0 2 2 2 2 2 2 解: 7.设随机变量X服从自由度为k的χ 2 分布,其概率密度 为: 其中k为正整数,求X的数学期望和方差。 = − − , . , ; ( ) ( / ) / / / 0 0 0 2 2 1 2 1 2 2 x x e x f x k k x k