
§2.3连续型随机变量 连续型随机变量X所有可能取值充满若 干个区间。对这种随机变量,不能象离散型 随机变量那样,指出其取各个值的概率,给 出概率分布。而是用“概率密度函数”表示 随机变量的概率分布
连续型随机变量X所有可能取值充满若 干个区间。对这种随机变量,不能象离散型 随机变量那样, 指出其取各个值的概率, 给 出概率分布。而是用“概率密度函数”表示 随机变量的概率分布。 §2.3 连续型随机变量

2.3.1频率直方图 例1:某工厂生产一种零件,由于生产过程中各 种随机因素的影响,零件长度不尽相同。现测 得该厂生产的100个零件长度(单位:mm)如下: 129,132,136,145,140,145,147,142,138,144,147,142,137,144,144, 134,149,142,137,137,155,128,143,144,148,139,143,142,135,142, 148,137,142,144,141,149,132,134,145,132,140,142,130,145,148, 143,148,135,136,152,141,146,138,131,138,136,144,142,142,137, 141,134,142,133,153,143,145,140,137,142,150,141,139,139,150, 139,137,139,140,143,149,136,142,134,146,145,130,136,140,134, 142,142,135,131,136,139,137,144,141,136. 这100个数据中,最小值是128,最大值是155
例1:某工厂生产一种零件,由于生产过程中各 种随机因素的影响,零件长度不尽相同。现测 得该厂生产的100个零件长度(单位: mm)如下: 2.3.1 频率直方图 129, 132, 136, 145, 140, 145, 147, 142, 138, 144, 147, 142, 137, 144, 144, 134, 149, 142, 137, 137, 155, 128, 143, 144, 148, 139, 143, 142, 135, 142, 148, 137, 142, 144, 141, 149, 132, 134, 145, 132, 140, 142, 130, 145, 148, 143, 148, 135, 136, 152, 141, 146, 138, 131, 138, 136, 144, 142, 142, 137, 141, 134, 142, 133, 153, 143, 145, 140, 137, 142, 150, 141, 139, 139, 150, 139, 137, 139, 140, 143, 149, 136, 142, 134, 146, 145, 130, 136, 140, 134, 142, 142, 135, 131, 136, 139, 137, 144, 141, 136. 这100个数据中,最小值是128,最大值是155。 155 128

作频率直方图的步骤 (1).先确定作图区间[a,们; a=最小数据-e/2,b=最大数据+ε/2, ε是数据的精度。 本例中8=1,a=127.5,b=155.5。 (2).确定数据分组数m=[1.87X(m-1)25+1] 组距d=(b-d/m, 子区间端点t=a+id,i=0,1,··,m
作频率直方图的步骤 (1). 先确定作图区间 [a, b] ; a = 最小数据-ε/ 2,b = 最大数据+ε/ 2, ε 是数据的精度。 本例中 ε = 1, a = 127.5, b = 155.5 。 (2). 确定数据分组数 m = [1.87×(n−1)2/5 + 1], 组距 d = (b − a) / m, 子区间端点t i = a + i d, i = 0, 1, · · · , m;
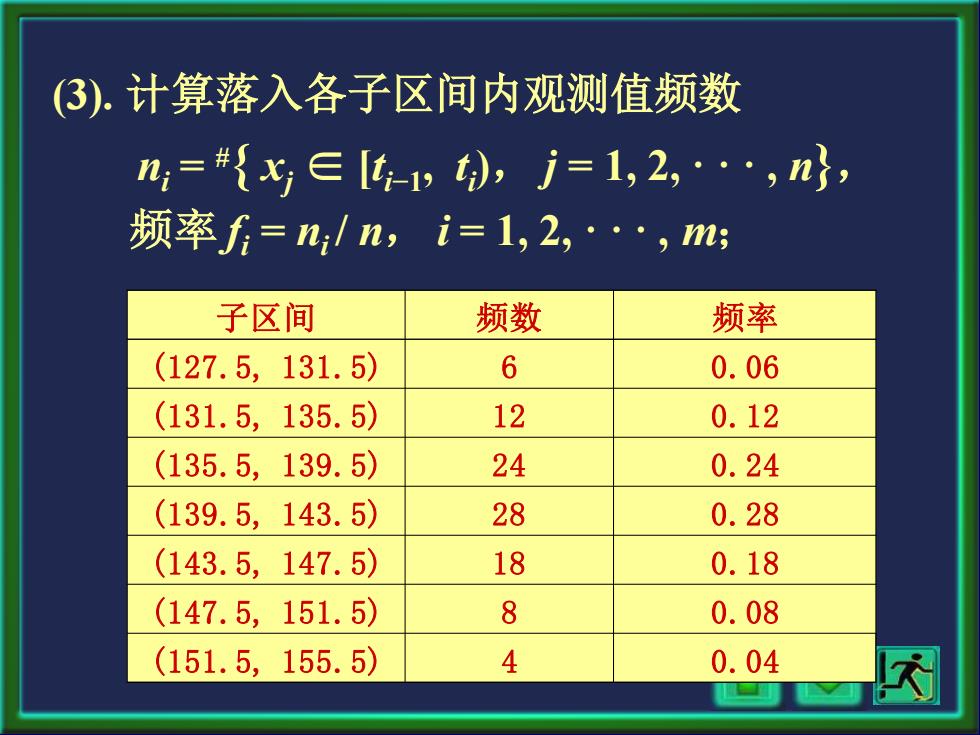
(3).计算落入各子区间内观测值频数 n=#{x,∈[t-1,t),j=1,2,··,n}, 频率f=n,/n,i=1,2,·,ms 子区间 频数 频率 (127.5,131.5) 6 0.06 (131.5,135.5) 12 0.12 (135.5,139.5) 24 0.24 (139.5,143.5) 28 0.28 (143.5,147.5) 18 0.18 (147.5,151.5) 8 0.08 (151.5,155.5) 4 0.04
(3). 计算落入各子区间内观测值频数 ni = #{ xj ∈ [t i−1, t i ), j = 1, 2, · · · , n}, 频率 fi = ni / n, i = 1, 2, · · · , m; 子区间 频数 频率 (127.5, 131.5) 6 0.06 (131.5, 135.5) 12 0.12 (135.5, 139.5) 24 0.24 (139.5, 143.5) 28 0.28 (143.5, 147.5) 18 0.18 (147.5, 151.5) 8 0.08 (151.5, 155.5) 4 0.04
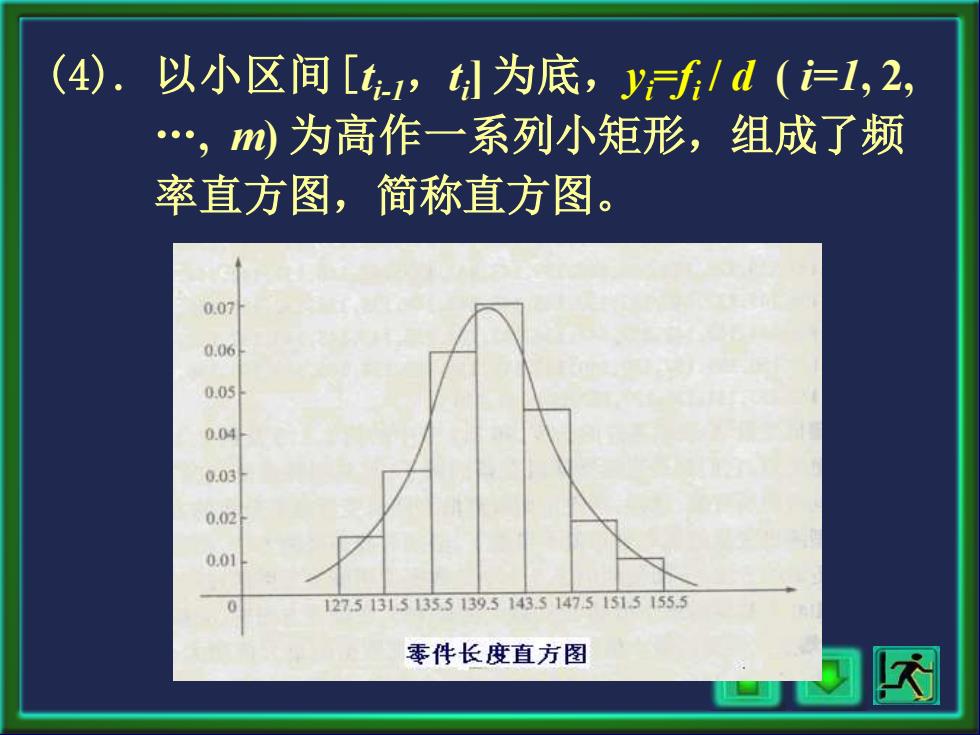
(4). 以小区间[,孙为底,yf1d(,2, .,m为高作一系列小矩形,组成了频 率直方图,简称直方图。 0.0 0.06 0.05 0.04 0.03 0.02 0.01 127513151355139.5143.5147.515151553 零件长度直方图 网
(4). 以小区间[t i-1,t i ] 为底,yi =fi / d ( i=1, 2, . , m) 为高作一系列小矩形,组成了频 率直方图,简称直方图

由于概率可以由频率近似,因此这个直 方图可近似地刻画零件长度的概率分布情况。 用上述直方图刻画随机变量的概率分布 情况是比较粗糙的。为更加准确地刻画的概 率分布情况,应适当增加观测数据的个数,同 时将数据分得更细一些。当数据越来越多,分 组越来越细时,直方图的上方外形轮廓就越来 越接近于某一条曲线,这条曲线称为随机变量 X的概率密度曲线,可用来准确地刻画X的概 率分布情况
由于概率可以由频率近似, 因此这个直 方图可近似地刻画零件长度的概率分布情况。 用上述直方图刻画随机变量X的概率分布 情况是比较粗糙的。为更加准确地刻画X的概 率分布情况,应适当增加观测数据的个数, 同 时将数据分得更细一些。当数据越来越多, 分 组越来越细时, 直方图的上方外形轮廓就越来 越接近于某一条曲线, 这条曲线称为随机变量 X的概率密度曲线,可用来准确地刻画X的概 率分布情况

2.3.2概率密度函数 定义1:若存在非负可积函数x),使随机 变量取值于任一区间(4,b]的概率可表示成 P(a<X≤b)=fx)dk. 则称X为连续型随机变量,x)为X的概率密 度函数,简称概率密度或密度。 @@的
2.3. 2 概率密度函数 定义1:若存在非负可积函数 f(x), 使随机 变量X取值于任一区间 (a, b] 的概率可表示成 ( ) ( ) , (1) = b a P a X b f x d x 则称 X为连续型随机变量, f(x)为 X 的概率密 度函数,简称概率密度或密度
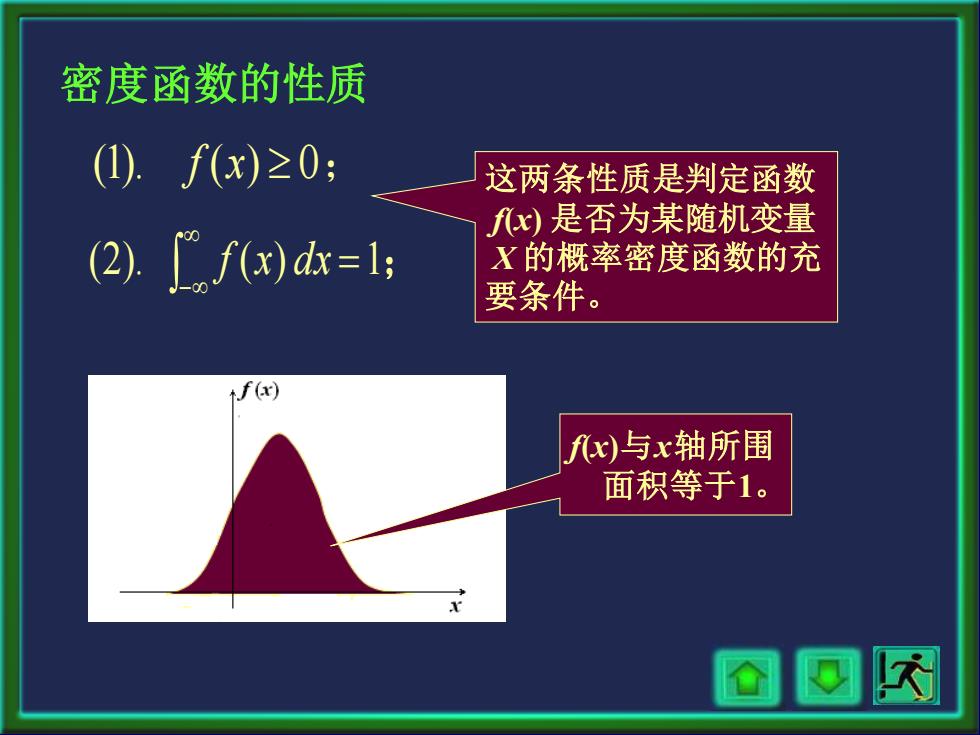
密度函数的性质 (I).f(x)≥0: 这两条性质是判定函数 )是否为某随机变量 (2).fx)dk=1; X的概率密度函数的充 要条件。 f(x) fx)与x轴所围 面积等于1。 容四网
这两条性质是判定函数 f(x) 是否为某随机变量 X 的概率密度函数的充 要条件。 密度函数的性质 (1). f (x) 0; (2). ( ) 1; − f x dx = f(x)与x轴所围 面积等于1

(3).对x)的进一步理解: 若x是fx)的连续点,则 x+△x P(x<X≤x+△x) f(t)dt lim lim △x→0 △x △x→0 △X =fx), 故,X的概率密度函数fx)在x这一点的值,恰 好是X落在区间x,x+△x上的概率与区间长 度△x之比的极限。这里,如果把概率理解为 质量,fx)相当于物理学中的线密度
若x是 f(x)的连续点,则 x P x X x x x + → ( ) lim 0 x ( ) lim 0 = + → x x x x f t dt =f(x), (3). 对 f(x)的进一步理解: 故, X的概率密度函数f(x)在x 这一点的值, 恰 好是X 落在区间 [x , x +△x]上的概率与区间长 度△x 之比的极限。 这里, 如果把概率理解为 质量,f (x)相当于物理学中的线密度

f() 需要注意的是:概率密度函数fx)在点a处 取值,不是事件{X=的概率。但是,该值 越大,X在a点附近取值的概率越大
需要注意的是:概率密度函数f (x)在点a处 取值,不是事件 {X=a} 的概率。但是,该值 越大,X 在a点附近取值的概率越大