
第三章 一外段分方金的部的存在突理 §1.解的存在唯一性定理与逐步逼近法 2.解的延拓 §3.解对初值的连续性和可微性 结束 帮助■ 上一面回下一页 首页
结束 帮助 上一页 返回 下一页 目录 首页 §1. 解的存在唯一性定理与逐步逼近法 §2. 解的延拓 §3. 解对初值的连续性和可微性

§1.解的存在雅一性定理与逐步 通近法 讲授内容:一阶微分方程解的存在唯一性定理 与逐步逼近法 讲授重点:存在唯一性定理的证明 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 §1.解的存在唯一性定理与逐步 逼近法 讲授内容:一阶微分方程解的存在唯一性定理 与逐步逼近法 讲授重点: 存在唯一性定理的证明

31解的存在唯一性定理与逐步逼近法 上节我们已经讲了,对于初值问题 y'=f(x,y) (2.1) y(xo)=yo 首先我们研究这样两个问题有着特别重要的实际意义: (2.1)的解是否存在? 2.1)的解是否唯一?在什么条件下,初值问题的解 存在且唯一呢?本章的定理1解决了这一问题。 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 上节我们已经讲了,对于初值问题 首先我们研究这样两个问题有着特别重要的实际意义: = 0 0 = ( , ) (2.1) ( ) y f x y y x y §3.1 解的存在唯一性定理与逐步逼近法 (2.1) 的解是否存在? (2.1) 的解是否唯一? 在什么条件下,初值问题的解 存在且唯一呢?本章的定理1解决了这一问题

3.1解的存在唯一性定理与逐步逼近法 y'=f(x,y) (2.1) y(xo)=yo 设(2.1)中的f(x矩形域 R:x-x≤a,y-y≤b (2.2) 上连续、 如果对于所有的(x,y1),(x,y存在常数 使得L>0 fx,)-f(x,y2)≤Ly1-2 成立,则称f(x在)R上关于y满足Lipschitz条件.L称 Lipschitz常数。 例如,函数f(x,y)在区域: 1≤y≤,浦尽x≤2 Lipschitz条件。因为对V(x,M),(x,y铕∈R w网层去吉k月 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 f x y f x y L y y ( , ) ( , ) 1 2 1 2 − − 例如,函数 在区域: 上满足 Lipschitz条件。因为对 有 f x y y ( , ) = 1 2,0 2 y x 1 2 ( , ),( , ) x y x y R− − = − = − + 1 2 1 2 1 2 1 2 1 2 1 ( , ) ( , ) 2 y y f x y f x y y y y y y y 如果对于所有的 ( , ),( , ) x y x y R 1 2 存在常数 , 使得 L 0 设(2.1)中的 f x y ( , ) 在矩形域 − − 0 0 R x x a y y b : , (2.2) 上连续. 成立,则称 在 R上关于 y 满足Lipschitz 条件.L称 Lipschitz常数。 f x y ( , ) §3.1 解的存在唯一性定理与逐步逼近法 = 0 0 = ( , ) (2.1) ( ) y f x y y x y

31解的存在唯一性定理与逐步逼近法 y=f(x,y) (2.1) (o)=o 定理1如果(2.1)中的f(x,y)满足如下两个条件: ()在R中连续;(2)在R上关于y满足Lipschitzs条件, 则方程(2.1)存在唯一的解y=p(x),定义于区间x-x≤h 上连续且满足初始条件: P(xo)=Yo (2.3) b 这里 h=min(a, M=max f(x,y) (x,y)∈R 此定理的证明分了五个部分.由于直接由(2.1)证明有困难.所 以将问题转化,首先证明求(21)的解等价于求积分方程 y=yo+f(x,y)dx 的连续解.证明的第二部分到第五部分证明积分方程的解存在且唯 结束 帮助 上一返回下页 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 此定理的证明分了五个部分. 由于直接由(2.1)证明有困难. 所 以将问题转化, 首先证明求(2.1)的解等价于求积分方程 = + 0 0 ( , ) x x y y f x y dx 定理1. 如果(2.1)中的 满足如下两个条件: (1) 在R中连续;(2) 在R上关于y满足Lipschitz条件. 则方程 (2.1)存在唯一的解 ,定义于区间 上连续且满足初始条件 : f x y ( , ) y x = ( ) − 0 x x h 0 0 ( ) (2.3) x y = 的连续解. 证明的第二部分到第五部分证明积分方程的解存在且唯 一 . §3.1 解的存在唯一性定理与逐步逼近法 = = ( , ) min( , ), max ( , ) x y R b h a M f x y M 这里 = 0 0 = ( , ) (2.1) ( ) y f x y y x y

3.1解的存在唯一性定理与逐步逼近法 任取一个连续函数,(x)代入积分方程右端的>,得函数 9(x)=y+Jf(s,0,(s)函 注 这里取的P,(x的图象必须在区域R内.因此x-x≤h 时,必须有p,(x)-y≤b成立,否则fx,m,(x)有可能无定义 如果0(x)=(x),那么()就是积分方程的解。否则,再把 ,(x)代入积分方程中右端的y,得到 (可以证明p(x) ,(x)=+∫f(s,9s)b 在区域R内) 如果P2(x)三(x),那么9(x)就是积分方程的解,否则我们继 续这个步骤,一般地作函数 p(x)=y+f(s,pn1(s)达 (2.4) 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 任取一个连续函数 0 ( ) x 代入积分方程右端的 y , 得函数 = + ( ) 0 1 0 0 ( ) , ( ) x x x y f s s ds ( ) 0 2 0 1 ( ) , ( ) x x x y f s s ds = + 如果 那么 就是积分方程的解。否则,再把 代入积分方程中右端的 ,得到 1 0 ( ) ( ), x x 1 ( ) x y 0 ( ) x (可以证明 在区域R内) ( ) 1 x 如果 ,那么 就是积分方程的解,否则我们继 续这个步骤,一般地作函数 2 1 ( ) ( ) x x 1 ( ) x = + ( − ) 0 0 1 ( ) , ( ) (2.4) x n n x x y f s s ds 这里取的 的图象必须在区域R内. 因此 时, 必须有 否则 有可能无定义 − 0 x x h 0 0 ( ) x y b − 成立, 0 f x x ( , ( )) 0 注 ( ) x §3.1 解的存在唯一性定理与逐步逼近法

3.1解的存在唯一性定理与逐步逼近法 就得到连续函数序列: p1(x)3p2(x),.pn(x)y。 如果p+1(x)=pn(x)那么pn(x)就是积分方程的解。 如果始终不发生这种情况,可以证明函数,p2,P.一致 收敛于p(x),然后证明这个极限函数p(x)就是积分方程(2.4) 的解.此方法称为逐步逼近法;(2.4)称为第n次近似解。 以下只在右半区间[,七,+月上讨论,左半区间上的讨论类似 命题1.设y=p(x)是(2.1)定义于[x,x+止满足 0(x)=y0 (2.3) 的解,则y=p(x)是积分方程 y=+f(s,p(s)达 (2.5) 的定义在x,x+M上的连续解。反之,如果=p(x)是积分方程(2.5) 定义在[x。,x。+h]上的连续解,则y=(x是微分方程(2.1)定义在上 [x,x+列满足2.3)的解. 结束 帮助 首而
结束 帮助 上一页 返回 下一页 目录 首页 如果始终不发生这种情况,可以证明函数列 一致 收敛于 ,然后证明这个极限函数 就是积分方程(2.4) 的解.此方法称为逐步逼近法;(2.4)称为第n次近似解。 1 2 , ,., ,. n ( ) x ( ) x 就得到连续函数序列: 1 2 ( ), ( ),. ( ),. n x x x n n +1 ( ) ( ) x x = ( ) n 如果 ,那么 x 就是积分方程的解。 以下只在右半区间 x x h 0 0 , + 上讨论,左半区间上的讨论类似. §3.1 解的存在唯一性定理与逐步逼近法 y x =( ) y x =( ) + 0 0 [ , ] x x h = 0 0 ( ) (2.3) x y = + ( ) 0 0 , ( ) (2.5) x x y y f s s ds + 0 0 命题1. 设 是(2.1)定义于 [ , ] x x h 上满足 的解,则 是积分方程 的定义在 上的连续解。反之,如果 是积分方程(2.5) 定义在 上的连续解, 则 是微分方程(2.1)定义在上 满足(2.3)的解. y x = ( ) 0 0 [ , ] x x h + y x = ( ) 0 0 [ , ] x x h +
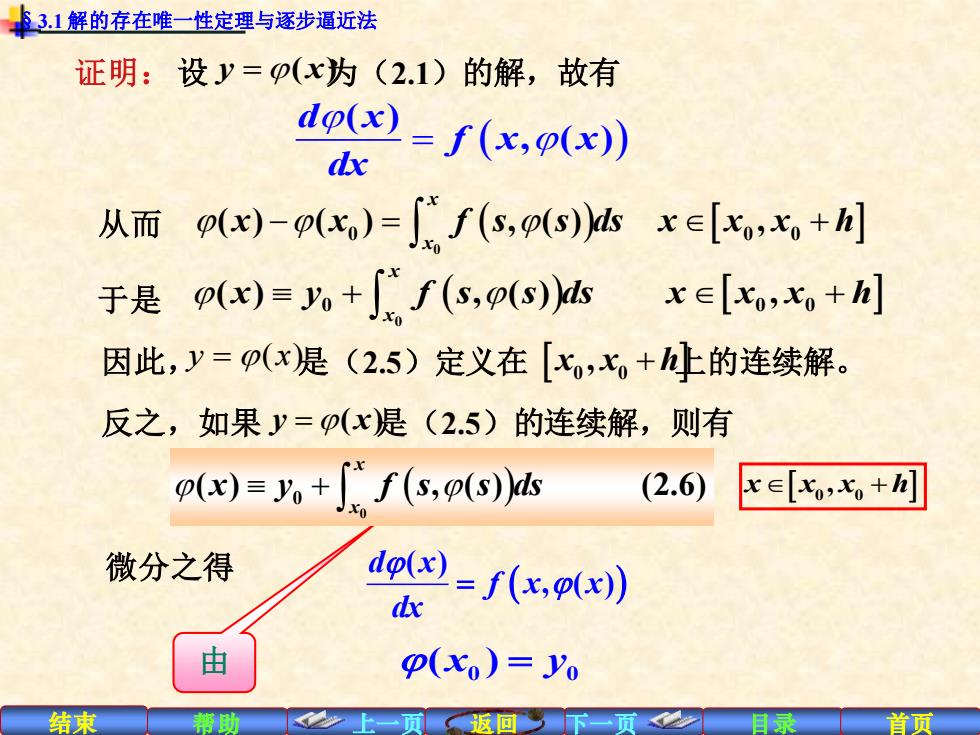
®31解的存在唯一性定理与逐步逼近法 证明:设y=p(x为(2.1)的解,故有 do)=f(x,p(x) dx 从而p()-(x,)=f(s,(s)hx∈[,七+ 于是(x)=+f(s,p(s) x∈[xo,x+h] 因此,y=(x是(2.5)定义在[七,七+的连续解。 反之,如果y=p(x是(2.5)的连续解,则有 (x)=yo+["f(s,o(s)ds (2.6 x∈[xo,x+h] 微分之得 do( d 2=f(x,p(x) 由 P(xo)=Yo 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 由 证明:设 y x =( ) 为(2.1)的解,故有 ( ) = ( ) , ( ) d x f x x dx 因此, y = (x) 是(2.5)定义在 x x h 0 0 , + 上的连续解。 反之,如果 y x =( ) 是(2.5)的连续解,则有 微分之得 ( ) ( ) , ( ) d x f x x dx = 0 0 ( ) x y = 于是 + + ( ) 0 0 0 0 ( ) , ( ) , x x x y f s s ds x x x h − = + ( ) 0 0 0 0 ( ) ( ) , ( ) , x x 从而 x x f s s ds x x x h + ( ) 0 0 ( ) , ( ) (2.6) x x x y f s s ds x x x h + 0 0 , §3.1 解的存在唯一性定理与逐步逼近法
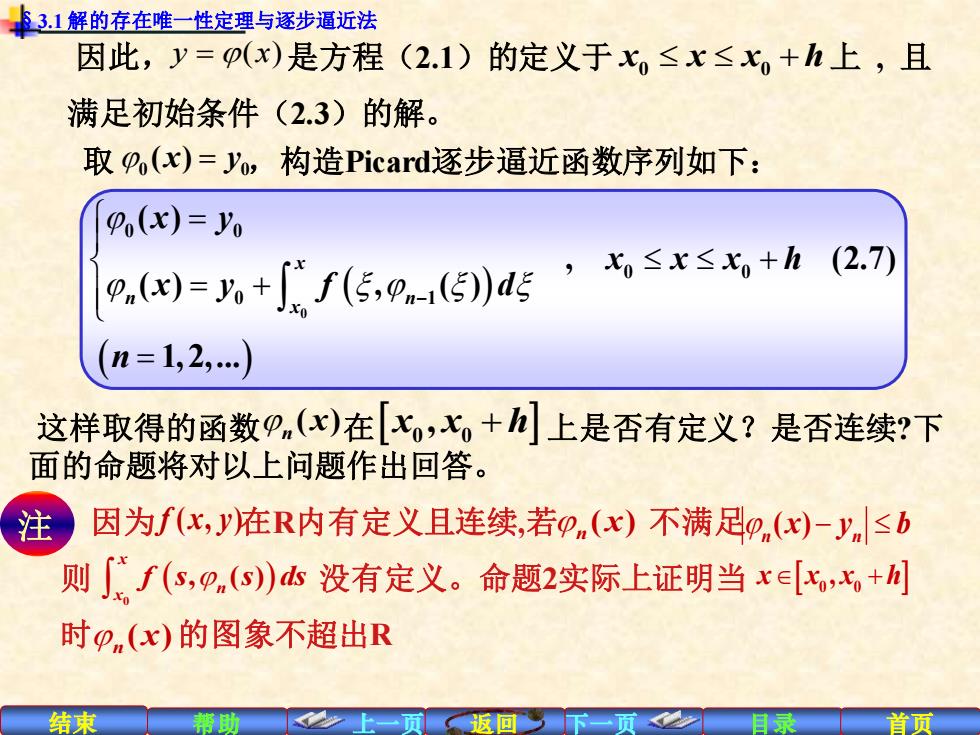
3.1解的存在唯一性定理与逐步逼近法 因此,y=p(x)是方程(2.1)的定义于x,≤x≤x,+h上,且 满足初始条件(2.3)的解。 取p(x)=yo,构造Picard逐步逼近函数序列如下: Po(x)=Yo .(=八+f((5,0n1传)d5’七≤x≤x+h(2.7 n=1,2,.) 这样取得的函数p(x)在[xo,x,+h上是否有定义?是否连续?下 面的命题将对以上问题作出回答。 注 因为fc,y在R内有定义且连续,若p(x)不满足D(x)-yn≤b 则∫f(s,p(s)心没有定义。命题2实际上证明当x∈[s,x+川 时p(x)的图象不超出R 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 因此, 是方程(2.1)的定义于 上 , 且 满足初始条件(2.3)的解。 y = (x) x x x h 0 0 + 取 0 0 ( ) x y = ,构造Picard逐步逼近函数序列如下: ( ) ( ) − = + = + = 0 0 0 0 0 0 1 ( ) , (2.7) ( ) , ( ) 1, 2,. x n n x x y x x x h x y f d n 这样取得的函数 在 上是否有定义?是否连续?下 面的命题将对以上问题作出回答。 因为 在R内有定义且连续,若 不满足 则 没有定义。命题2实际上证明当 时 的图象不超出R ( ) n x x x h 0 0 , + ( ) n x ( )− n n x y b ( ) 0 , ( ) x n x f s s ds x x x h + 0 0 , ( ) n x 注 f x y ( , ) §3.1 解的存在唯一性定理与逐步逼近法

3.1解的存在唯一性定理与逐步逼近法 命题2.对于所有的正整数n,(2.7)中的p(x)在[Xo,x,+h上有定义, 连续且满足 pn(x)-y≤b (2.8) 证明:用数学归纳法证明。当=1时 m,(x)=+Jf(5y)15 ,(x)在[x,x+小上有定义,连续且 lA,(x)-l≤f5,)lh5≤M(x-x)≤Mh≤b 即命题2当n=1时成立.设当=k时,p(x)在[xo,x+h上有定 义,连续且满足 9(x)-ya≤b 这时 P+1(x)=o+f(5,P(5)15 结束 帮助 返叵
结束 帮助 上一页 返回 下一页 目录 首页 命题2. 对于所有的正整数n, (2.7)中的 在 上有定义, 连续且满足 ( ) n x x x h 0 0 , + − 0 n ( ) 2.8 x y b ( ) 证明:用数学归纳法证明。当n=1 时 ( ) 0 1 0 0 ( ) , x x x y f y d = + 1 ( ) x 在 x x h 0 0 , + 上有定义,连续且 1 0 ( ) x y − 即命题2 当 n=1 时成立. 设当n=k时, 在 上有定 义,连续且满足 ( ) k x x x h 0 0 , + − 0 ( ) k x y b ( ) 0 1 0 ( ) , ( ) x k k x + x y f d = + 这时 §3.1 解的存在唯一性定理与逐步逼近法 0 0 ( , ) x x f y d − M x x Mh ( 0 ) b