
第九章机械中的摩擦和效率 内容提要 本章主要介绍运动副中的摩擦,考虑摩擦时机构的受力分析以及与摩擦有关的机械效率的 计算、自锁条件的判定问题,最后介绍提高机械效率的途径。 9.1概述 运动副作为机构运动和动力传递的媒介,运动副元素之间的一切直接接触在构件具有相对运 动和运动趋势时,必然会产生摩擦力。机构运转过程中,各运动副中的摩擦力是一种有害的阻力, 它一方面消耗输入功,造成动力浪费,降低机械效率:另一方面造成运动副元素磨损,从而削弱 零件强度,降低机械运动精度、可靠性和使用寿命:此外摩擦还会使运动副温度升高,破坏正常 的润滑条件,出现配合性质变化甚至卡死现象,使机械无法正常工作。据资料统计,世界能源约 有13-1/2消耗于摩擦,报废机械零件中约80%是由于磨损引起的。 通常,机械中的摩擦超大,效率越低。当低到一定程度时,机械就会出现自锁。所以摩擦、 效率和自锁是一个问题的三个方面,其中心问题是摩擦。因此,本章主要研究常见运动副中的摩 擦、效率和自锁问题。 需要注意的是,摩擦也有可利用的一面。主要表现为,可以利用摩擦传递动力和能量,例如 摩擦轮传动、带传动、摩擦离合器、制动器、需要自锁的机械等。 9.2运动副中的摩擦 在平面机构中,常见的运动副有移动副、转动副和高副三种。其中属于低副的移动副和转动 副中只有滑动摩擦产生,而高副中既有滑动摩擦又有滚动摩擦,由于滚动摩擦较滑动摩擦小很多, 故常常忽略不计,所以对高副中的摩擦分析同移动副摩擦一样。 讨论运动副中的摩擦,重要的工作是确定运动副中总反力的大小、方向及作用点位置,从而 可以方便地判断它们对构件运动和受力的影响。 9.2.1移动副中的摩擦 移动副中的摩擦是运动副摩擦的一种简单的方式,广泛存在于机械运动中。常见的有三种情 196
196 第九章 机械中的摩擦和效率 内容提要 本章主要介绍运动副中的摩擦,考虑摩擦时机构的受力分析以及与摩擦有关的机械效率的 计算、自锁条件的判定问题,最后介绍提高机械效率的途径。 9.1 概述 运动副作为机构运动和动力传递的媒介,运动副元素之间的一切直接接触在构件具有相对运 动和运动趋势时,必然会产生摩擦力。机构运转过程中,各运动副中的摩擦力是一种有害的阻力, 它一方面消耗输入功,造成动力浪费,降低机械效率;另一方面造成运动副元素磨损,从而削弱 零件强度,降低机械运动精度、可靠性和使用寿命;此外摩擦还会使运动副温度升高,破坏正常 的润滑条件,出现配合性质变化甚至卡死现象,使机械无法正常工作。据资料统计,世界能源约 有 1/3~1/2 消耗于摩擦,报废机械零件中约 80%是由于磨损引起的。 通常,机械中的摩擦越大,效率越低。当低到一定程度时,机械就会出现自锁。所以摩擦、 效率和自锁是一个问题的三个方面,其中心问题是摩擦。因此,本章主要研究常见运动副中的摩 擦、效率和自锁问题。 需要注意的是,摩擦也有可利用的一面。主要表现为,可以利用摩擦传递动力和能量,例如 摩擦轮传动、带传动、摩擦离合器、制动器、需要自锁的机械等。 9.2 运动副中的摩擦 在平面机构中,常见的运动副有移动副、转动副和高副三种。其中属于低副的移动副和转动 副中只有滑动摩擦产生,而高副中既有滑动摩擦又有滚动摩擦,由于滚动摩擦较滑动摩擦小很多, 故常常忽略不计,所以对高副中的摩擦分析同移动副摩擦一样。 讨论运动副中的摩擦,重要的工作是确定运动副中总反力的大小、方向及作用点位置,从而 可以方便地判断它们对构件运动和受力的影响。 9.2.1 移动副中的摩擦 移动副中的摩擦是运动副摩擦的一种简单的方式,广泛存在于机械运动中。常见的有三种情

况,即平面摩擦、斜面摩擦和槽面摩擦。 1.平面摩擦 如图91所示,滑块1与水平面2构成的移动副,滑块在铅 垂载荷Q(包括自重)和水平驱动力F的作用下向右匀速运动。 平面2对滑块1产生的反力有法向反力N21和摩擦力F21,由库 仑定律可知F,=N21,式中f为摩擦系数(coefficient of friction), 可从机械设计手册中查取),其方向与滑块1相对运动方向2相 反,如图所示。 法向反力N21与摩擦力F,的合力R21为平面2对滑块1的总 反力(total reaction)。总反力R2,与法向反力N21之间的夹角p称 图91平面摩擦 为摩擦角(angle of friction)。 o=arctanf (9.1) 由上述分析可知,总反力R2!的方向永远与相对运动”2的方向成90°+Q的钝角,可利用这 规律来确定移动副中总反力的方向。 2。斜面磨容 如图9-2a所示,将滑块1置于倾角为α的斜面2上,其上作用有铅锤载荷Q。下面分析使 滑块1沿斜面2等速运动时所需水平力的大小。 1)滑块等速上升 当滑块1在水平力F作用下沿斜面2等速上升时,斜面2作用于滑块1的总反力为R2,(与 2的方向成90°+0的纯角),根据滑块受力平衡的条件可得 F+O+R1=0 式中的只有F与R,的大小未知。可通过作力的三角形图(如图9-2b所示),求得水平驱动力F 的大小为 F=Otan(a+o) (9-2) 2)滑块等速下滑 a
197 况,即平面摩擦、斜面摩擦和槽面摩擦。 1.平面摩擦 如图 9-1 所示,滑块 1 与水平面 2 构成的移动副,滑块在铅 垂载荷 Q(包括自重)和水平驱动力 F 的作用下向右匀速运动。 平面 2 对滑块 1 产生的反力有法向反力 N21 和摩擦力 F21,由库 仑定律可知 21 21 F = fN ,式中 f 为摩擦系数(coefficient of friction), 可从机械设计手册中查取),其方向与滑块 1 相对运动方向 12 v 相 反,如图所示。 法向反力 N21 与摩擦力 F21 的合力 R21 为平面 2 对滑块 1 的总 反力(total reaction)。总反力 R21 与法向反力 N21 之间的夹角 称 为摩擦角(angle of friction)。 = arctan f (9-1) 由上述分析可知,总反力 R21 的方向永远与相对运动 12 v 的方向成 + 90 的钝角,可利用这 一规律来确定移动副中总反力的方向。 2.斜面摩擦 如图 9-2a 所示,将滑块 1 置于倾角为 的斜面 2 上,其上作用有铅锤载荷 Q。下面分析使 滑块 1 沿斜面 2 等速运动时所需水平力的大小。 1)滑块等速上升 当滑块 1 在水平力 F 作用下沿斜面 2 等速上升时,斜面 2 作用于滑块 1 的总反力为 R21 (与 12 v 的方向成 + 90 的钝角),根据滑块受力平衡的条件可得 F + Q + R21 = 0 式中的只有 F 与 R21 的大小未知。可通过作力的三角形图(如图 9-2b 所示),求得水平驱动力 F 的大小为 F = Q tan( +) (9-2) 2)滑块等速下滑 (a) (b) (a) (b) 图 9-1 平面摩擦

图9-2滑块等速上升 图9-3滑块等速下滑 如图9-3所示,当滑块1在水平力F作用下沿斜面2等速下滑时,斜面2作用于滑块1的 总反力为R,(与v,的方向成90°+的钝角),根据滑块受力平衡的条件可得 F+0+R1=0 式中只有F与R2,的大小未知。同理,通过作力的三角形图(如图93b所示),求得水平驱动力 F的大小 F=Otan(a-0) (9.3) 值得注意的是,当滑块1等速上滑时,力F为驱动力:而当滑块1下滑时,F为阻抗力, 其作用是阻止滑块1加速下滑。如果把力F为驱动力的行程称为正行程:把力F为阻抗力的行 程称为反行程。由式(9-2)和式(9-3)可知,当已经列出了正行程的关系式时,只需将摩擦角 的符号改变,便可以得到反行程的关系式。 3槽面摩擦 如图9-4a所示,楔形滑块1放在夹角为28的槽面2上,在水平驱动力作用下,沿着槽面等 速滑动。Q为作用在滑块上的铅垂载荷,N2,为槽面给滑块1的法向反力。根据楔形块1在铅垂 方向受力平衡,如图94b所示,可得 故摩擦力的大小为 F=N-/品。 若令 (9-4) 色 F=fO (9-5) 式中,人,称当量摩擦系数(equivalent of friction),相当于把楔形滑块视为平滑块时的 摩擦系数。与之对应的摩擦角g,=arctan∫称为当量摩擦角(equivalent angle of friction)。 (a) (b) 198
198 图 9-2 滑块等速上升 图 9-3 滑块等速下滑 如图 9-3a 所示,当滑块 1 在水平力 F' 作用下沿斜面 2 等速下滑时,斜面 2 作用于滑块 1 的 总反力为 ' R21 (与 12 v 的方向成 + 90 的钝角),根据滑块受力平衡的条件可得 F ' + Q + R21 = 0 式中只有 F' 与 R21 的大小未知。同理,通过作力的三角形图(如图 9-3b 所示),求得水平驱动力 F' 的大小 F' = Qtan( −) (9-3) 值得注意的是,当滑块 1 等速上滑时,力 F 为驱动力;而当滑块 1 下滑时, F' 为阻抗力, 其作用是阻止滑块 1 加速下滑。如果把力 F 为驱动力的行程称为正行程;把力 F' 为阻抗力的行 程称为反行程。由式(9-2)和式(9-3)可知,当已经列出了正行程的关系式时,只需将摩擦角 的符号改变,便可以得到反行程的关系式。 3.槽面摩擦 如图 9-4a 所示,楔形滑块 1 放在夹角为 2 的槽面 2 上,在水平驱动力作用下,沿着槽面等 速滑动。Q 为作用在滑块上的铅垂载荷, N21 为槽面给滑块 1 的法向反力。根据楔形块 1 在铅垂 方向受力平衡,如图 9-4b 所示,可得 21 sin Q N = 故摩擦力的大小为 21 21 sin Q F fN f = = 若令 v sin f f = (9-4) 则 F21 = f vQ (9-5) 式中, v f 称当量摩擦系数(equivalent coefficient of friction),相当于把楔形滑块视为平滑块时的 摩擦系数。与之对应的摩擦角 v v = arctan f 称为当量摩擦角(equivalent angle of friction)。 (a) (b)

图94槽面摩擅 般情况下0≤90°,所以人>∫,即楔形滑块比平面滑块的摩擦力大,因此常用楔形来增 大所需的摩擦力。V带传动、三角螺纹就是应用实例。需要指出的是,上述摩擦力的增大并不是 因为运动副元素材料间的摩擦系数发生了变化,而是因为运动副元素的几何结构形状发生了变化 致使正压力变大。 引入当量摩擦系数以后,在分析运动副中的滑动摩擦力时,不管运动副两元素的几何形状如 何,均可视为单一平面接触来计算其摩擦力,即只需按运动副元素几何形状的不同引入不同的当 量摩擦系数即可。 9.2.2螺旋副中的摩擦 如图9-5所示,当螺杆1和螺母2的螺纹之间受轴向载荷Q时,拧动螺杆或螺母,螺旋面 之间将产生摩擦力。假设轴向载荷Q集中作用于螺纹中径山上,而螺杆1的螺纹可以假想是由 一斜面卷绕在圆柱体上形成的,所以螺母和螺杆的相互作用可以简化为滑块和斜面的相互作用关 系,如图95b所示,这样就可以把空间问题转化为平面问题来研究。下面就矩形螺纹螺旋副中 的摩擦和三角形螺纹螺旋副中的摩擦进行讨论。 1.矩形螺纹螺旋副中的摩擦 22,-1 Te/2 (a) (b) 图95矩形螺纹螺旋副中的摩擦 如图95所示的矩形螺旋副中,可得 tana=- nd2 nd2 式中,α为螺纹在中径处的升角::为螺纹的线数:P,为螺距:I为螺纹的导程。 当拧紧螺母时,即逆着Q的方向等速向上运动时,相当于滑块1沿斜面2等速上升的过程, 故作用在螺纹中径山,上的圆周力F相当于作用于滑块上的水平力F F=Otan(a+) 故拧紧螺母时所需的力矩为 199
199 图 9-4 槽面摩擦 一般情况下 90 ,所以 f f v ,即楔形滑块比平面滑块的摩擦力大,因此常用楔形来增 大所需的摩擦力。V 带传动、三角螺纹就是应用实例。需要指出的是,上述摩擦力的增大并不是 因为运动副元素材料间的摩擦系数发生了变化,而是因为运动副元素的几何结构形状发生了变化 致使正压力变大。 引入当量摩擦系数以后,在分析运动副中的滑动摩擦力时,不管运动副两元素的几何形状如 何,均可视为单一平面接触来计算其摩擦力,即只需按运动副元素几何形状的不同引入不同的当 量摩擦系数即可。 9.2.2 螺旋副中的摩擦 如图 9-5a 所示,当螺杆 1 和螺母 2 的螺纹之间受轴向载荷 Q 时,拧动螺杆或螺母,螺旋面 之间将产生摩擦力。假设轴向载荷 Q 集中作用于螺纹中径 2 d 上,而螺杆 1 的螺纹可以假想是由 一斜面卷绕在圆柱体上形成的,所以螺母和螺杆的相互作用可以简化为滑块和斜面的相互作用关 系,如图 9-5b 所示,这样就可以把空间问题转化为平面问题来研究。下面就矩形螺纹螺旋副中 的摩擦和三角形螺纹螺旋副中的摩擦进行讨论。 1.矩形螺纹螺旋副中的摩擦 (a) (b) 图 9-5 矩形螺纹螺旋副中的摩擦 如图 9-5 所示的矩形螺旋副中,可得 2 h 2 tan d zP d l = = 式中, 为螺纹在中径处的升角;z 为螺纹的线数; Ph 为螺距; l 为螺纹的导程。 当拧紧螺母时,即逆着 Q 的方向等速向上运动时,相当于滑块 1 沿斜面 2 等速上升的过程, 故作用在螺纹中径 2 d 上的圆周力 F 相当于作用于滑块上的水平力 F F = Q tan( +) 故拧紧螺母时所需的力矩为

M=Fd=d Quan(a+ (9-6) 当放松螺母时,即顺着Q的方向等速向下运动时,相当于滑块1沿斜面2等速下降的过程,故 放松螺母时的力矩为 F'受-受0ma-p (9-7) 2 2.三角形螺纹螺旋副中的摩擦 如图96所示,三角形螺纹螺旋刷和矩形螺纹螺旋剧的风 别在于螺纹间接触面的形状不同。螺母在螺杆上的运动与楔形 滑块沿斜槽面的运动相似,利用当量摩擦系数的概念,由式 (94)得 式中,B为牙侧角。从而 .c 图96三角形螺纹螺旋副中的摩 将,代入式(9-6)可得,拧紧三角形螺纹螺母时,所需的力矩为 M=F=Qtan(a+,) (9-8) 将,代入式(97)可得,当放松三角形螺纹螺母时,所需的力矩为 =F-受Qtma-a) (9-9) 由于口,>口,故三角形螺纹的摩擦力矩比矩形螺纹较大,宜用于联接紧固:矩形螺纹摩擦力 矩较小,效率高,宜用于传递动力的场合。 9.2.3转动副中的摩擦 转动副在各种机械中应用很广,常见的有轴和轴承以及各种铰链。转动副可按载荷作用情况 的不同分成径向轴颈与轴承和止推轴颈与轴承。下面来讨论如何计算轴承对轴径的摩擦力及摩擦 力矩,以及考虑摩擦时转动副中总反力的方位的确定方法。 1.径向轴颈与轴承的摩擦 如图97为径向轴颈与轴承摩擦,设轴颈1受径向载荷Q,在驱动力偶矩M:的作用下,在 轴承中匀速转动。 根据平衡条件,轴承2对轴径1的所有法向反力和摩擦力合成后的总反力R,必与Q等值反 向(即风=),而R1与Q必组成一对力偶,此力偶即为摩擦力偶,其力偶矩M:必与M:等 值反向(即M=-M:)。如图97b所示,可得力臂为 p M:Ma 200
200 tan( ) 2 2 2 2 = = Q + d d M F (9-6) 当放松螺母时,即顺着 Q 的方向等速向下运动时,相当于滑块 1 沿斜面 2 等速下降的过程,故 放松螺母时的力矩为 tan( ) 2 2 ' ' 2 2 = = Q − d d M F (9-7) 2.三角形螺纹螺旋副中的摩擦 如图 9-6 所示,三角形螺纹螺旋副和矩形螺纹螺旋副的区 别在于螺纹间接触面的形状不同。螺母在螺杆上的运动与楔形 滑块沿斜槽面的运动相似,利用当量摩擦系数的概念,由式 (9-4)得 sin(90 ) cos v f f f = − = 式中, 为牙侧角。从而 ) cos arctan( v f = 将 v 代入式(9-6)可得,拧紧三角形螺纹螺母时,所需的力矩为 tan( ) 2 2 v 2 2 = = Q + d d M F (9-8) 将 v 代入式(9-7)可得,当放松三角形螺纹螺母时,所需的力矩为 tan( ) 2 2 ' ' v 2 2 = = Q − d d M F (9-9) 由于 v ,故三角形螺纹的摩擦力矩比矩形螺纹较大,宜用于联接紧固;矩形螺纹摩擦力 矩较小,效率高,宜用于传递动力的场合。 9.2.3 转动副中的摩擦 转动副在各种机械中应用很广,常见的有轴和轴承以及各种铰链。转动副可按载荷作用情况 的不同分成径向轴颈与轴承和止推轴颈与轴承。下面来讨论如何计算轴承对轴径的摩擦力及摩擦 力矩,以及考虑摩擦时转动副中总反力的方位的确定方法。 1.径向轴颈与轴承的摩擦 如图 9-7 为径向轴颈与轴承摩擦,设轴颈 1 受径向载荷 Q,在驱动力偶矩 Md 的作用下,在 轴承中匀速转动。 根据平衡条件,轴承 2 对轴径 1 的所有法向反力和摩擦力合成后的总反力 R21 必与 Q 等值反 向(即 R21 = −Q ),而 R21 与 Q 必组成一对力偶,此力偶即为摩擦力偶,其力偶矩 M f 必与 Md 等 值反向(即 Mf = −Md )。如图 9-7b 所示,可得力臂为 Q M R M d 21 f = = 图 9-6 三角形螺纹螺旋副中的摩擦

将R,在其作用线与轴径的交点处分解为通过轴心O和相切于轴径的两个分力N,和F1,因 N2对轴心O的力矩为零,故 M=Fr=人Qr=人R2r=R2P 整理后可得 p=∫r (9-10) 上式表明,的大小与轴径半径r和当量摩擦系数人有关。对于具体的轴颈,p为定值。以 轴颈中心0为圆心,p为半径作的圆(如图97b虚线所示),称为摩擦圆,p称为摩擦圆半径。 当量摩擦系数人=(1~π/2)∫,对于紧密配合未经跑合的转动副取较大值,对于有较大间隙的松 配合传动副取较小值。 由以上分析可知,总反力R,始终切于摩擦圆,大小与载荷Q相等:其对轴颈轴心O的力矩 方向必与轴颈相对于轴承的角速度2的方向相反。 Ma (a) (b) 图97径向轴颈与轴承的摩擦 2.止推轴颈与轴承的摩擦 轴用以承受轴向载荷的部分称为轴端或轴踵。如图9-8所示,轴端1和承受轴向载荷的止推 轴承2构成一转动副,当轴转动时接触面间将产生摩擦力,摩擦力对回转轴线之矩即为摩擦力矩 M。 如图9-8所示,从轴端半径为p处,取宽度为dp的环形微面积ds=2dp,设其上的压强p 为常数,则环形微面积上所受正压力dN=pds,摩擦力为dF=N=ds,对回转轴线的摩擦 力矩为 dMs =pdF pfpds=2fpdo 轴端上所受的总摩擦力矩为 M=2对fp2pdp 2R 对于式(911)的解需分两种情况讨论 (1)非跑合的新止推轴承,各处压强基本相等,可得 201 图9-8止推轴颈与轴承的摩擦
201 将 R21 在其作用线与轴径的交点处分解为通过轴心 O 和相切于轴径的两个分力 N21 和 F21,因 N21 对轴心 O 的力矩为零,故 M f = F21r = f vQr = f vR21r = R21 整理后可得 f r = v (9-10) 上式表明, 的大小与轴径半径 r 和当量摩擦系数 v f 有关。对于具体的轴颈, 为定值。以 轴颈中心 O 为圆心, 为半径作的圆(如图 9-7b 虚线所示),称为摩擦圆, 称为摩擦圆半径。 当量摩擦系数 f (1 ~ / 2) f v = ,对于紧密配合未经跑合的转动副取较大值,对于有较大间隙的松 配合传动副取较小值。 由以上分析可知,总反力 R21 始终切于摩擦圆,大小与载荷 Q 相等;其对轴颈轴心 O 的力矩 方向必与轴颈相对于轴承的角速度 12 的方向相反。 (a) (b) 图 9-7 径向轴颈与轴承的摩擦 2.止推轴颈与轴承的摩擦 轴用以承受轴向载荷的部分称为轴端或轴踵。如图 9-8 所示,轴端 1 和承受轴向载荷的止推 轴承 2 构成一转动副,当轴转动时接触面间将产生摩擦力,摩擦力对回转轴线之矩即为摩擦力矩 Mf。 如图 9-8 所示,从轴端半径为 处,取宽度为 d 的环形微面积 ds = 2d ,设其上的压强 p 为常数,则环形微面积上所受正压力 d ds N p = ,摩擦力为 dF = fdN = fpds ,对回转轴线的摩擦 力矩为 d d d 2 d 2 f M = F = f p s = f p 轴端上所受的总摩擦力矩为 = R r M 2f pd 2 f (9-11) 对于式(9-11)的解需分两种情况讨论: (1)非跑合的新止推轴承,各处压强基本相等,可得 图 9-8 止推轴颈与轴承的摩擦

M-号e是子 (9-12) (2)跑合的止推轴承,各处的压强不相等,离中心远的地方磨损较快,因而压强减小:离 中心近的部分磨损较慢,因而压强增大,近似符合p印=常数。可得 M=e生 (9.13) 因为p=常数,所以轴端轴心处的压强将非常大,很容易损坏,故实际应用中一般采用空 心轴端。 在会分析运动副中总反力基础上,就不难在考虑摩擦的条件对机构进行受力分析,下面举例 加以说明。 【例9-1】如图99a所示的曲柄滑块机构,已知各构件的尺寸,各转动副的半径r,各运动 副的摩擦系数作用在滑块上生产阻力Q,在不计各构件质量的情况下,求机构在图示位置时 各运动副中的总反力及作用在曲柄1上的驱动力偶矩M。 解:此题为考虑摩擦时含转动副和移动副的机构静力分析问题。首先应从受力最简单的二力 杆2进行分析,然后根据构件间相对运动情况得出总反力的方向及位置:再利用其它构件受力平 衡,结合已知力求出未知力的大小。 (1)由已知条件得转动副的摩擦圆半径P=∫r,从而确定转动副A、B、C三处的摩擦圆, 如图9-9所示:然后求出运动副的摩擦角p=arctanf。 (2)分析二力杆的受力。不计质量时,杆2为不含力偶的二力杆。由图所示的驱动力偶矩M 和生产阻力F的方向易知,杆2受压力,总反力R=-R,且这二力必定与各处摩擦圆相切, 由⊙1的方向知,在转动副B处,构件1、2的夹角为变大趋势:在转动副C处构件2、3之间的 夹角为变小趋势。所以相对转动角速度021、2:的方向均为逆时针,故可确定R12和R2位于如 图99外所示的两摩擦圆的内公切线上。 (3)滑块3的受力分析。如图99%所示滑块受有三个力,即工作阻力F、杆2对滑块的总 反力R2,和机架对滑块的总反力R3。而R2=-R2。需要确定R,方向及作用点位置,由于4水 平向右,所以R,与y:的方向偏移90°+0,即由法线方向左偏转一摩擦角,根据三力平衡必定 汇交的原则,R,必通过F和R:作用线的汇交点。在这三个力中只有R:和R,的大小未知,因 此作力的三角形可求,如图9-9c所示。 、2 2 C3 9 R 0 4 R43 (a) (b) (c) 图9-9曲柄滑块机构 (4)分析曲柄1的受力。曲柄1的受力分析如图9%所示,为含力偶的二力杆,在转动副 202
202 2 2 3 3 f 3 2 R r R r M fQ − − = (9-12) (2)跑合的止推轴承,各处的压强不相等,离中心远的地方磨损较快,因而压强减小;离 中心近的部分磨损较慢,因而压强增大,近似符合 p = 常数 。可得 2 f R r M fQ + = (9-13) 因为 p = 常数 ,所以轴端轴心处的压强将非常大,很容易损坏,故实际应用中一般采用空 心轴端。 在会分析运动副中总反力基础上,就不难在考虑摩擦的条件对机构进行受力分析,下面举例 加以说明。 【例 9-1】如图 9-9a 所示的曲柄滑块机构,已知各构件的尺寸,各转动副的半径 r ,各运动 副的摩擦系数 f,作用在滑块上生产阻力 Q,在不计各构件质量的情况下,求机构在图示位置时 各运动副中的总反力及作用在曲柄 1 上的驱动力偶矩 M1。 解:此题为考虑摩擦时含转动副和移动副的机构静力分析问题。首先应从受力最简单的二力 杆 2 进行分析,然后根据构件间相对运动情况得出总反力的方向及位置;再利用其它构件受力平 衡,结合已知力求出未知力的大小。 (1)由已知条件得转动副的摩擦圆半径 f r = v ,从而确定转动副 A、B、C 三处的摩擦圆, 如图 9-9b 所示;然后求出运动副的摩擦角 = arctan f 。 (2)分析二力杆的受力。不计质量时,杆 2 为不含力偶的二力杆。由图所示的驱动力偶矩 M1 和生产阻力 F 的方向易知,杆 2 受压力,总反力 R12 = −R32 ,且这二力必定与各处摩擦圆相切。 由 1 的方向知,在转动副 B 处,构件 1、2 的夹角为变大趋势;在转动副 C 处构件 2、3 之间的 夹角为变小趋势。所以相对转动角速度 21、23 的方向均为逆时针,故可确定 R12 和 R32 位于如 图 9-9b 所示的两摩擦圆的内公切线上。 (3)滑块 3 的受力分析。如图 9-9b 所示滑块受有三个力,即工作阻力 F、杆 2 对滑块的总 反力 R23 和机架对滑块的总反力 R43。而 R23 = −R32 。需要确定 R43 方向及作用点位置,由于 34 v 水 平向右,所以 R43 与 34 v 的方向偏移 + 90 ,即由法线方向左偏转一摩擦角,根据三力平衡必定 汇交的原则, R43 必通过 F 和 R23 作用线的汇交点。在这三个力中只有 R23 和 R43 的大小未知,因 此作力的三角形可求,如图 9-9c 所示。 (a) (b) (c) 图 9-9 曲柄滑块机构 (4)分析曲柄 1 的受力。曲柄 1 的受力分析如图 9-9b 所示,为含力偶的二力杆,在转动副

A、B处有机架4和连杆2对曲柄的总反力R,和R1。根据作用力与反作用力原理,即可确定R2! 的方向和位置。由于R41对中心A产生的摩擦力矩一定与曲柄相对机架的转动角速度方向相反, 可以确定R,位于摩擦圆的下方。根据曲柄上只受有两个总反力R,和R,和一个驱动力偶矩M, 因此,可知R1一定与R,平行、方向相反,组成一个阻力偶矩与驱动力偶矩M,平衡。从而可求 得M的大小。 9.3机械的效率和自锁 9.3.1机械的效率及表达形式 1.效率以功或功率的形式表达 根据能量守恒定理,机械稳定运转时,输入功W:等于输出功W,和损耗功W之和,即 形a=形,+W (9-14) 通常,把机械的输出功围,和输入功形的比值称为机械效率,即 n=W/Wa=1-W:/Wa (9-15) 它反映了输入功在机械中有效利用程度。 将式(914)的等号两端和式(915)的分子、分母各除以做功的时间1,可得 P=P+P (9-16) n=P/P=1-P:/Pa (9-17) 式中,P、P、P分别为输入功率、输出功率和损耗功率。 由于损耗功率不可能为零,所以机械的效率总是小于1。为提高机械效率,应尽量减少机械 中的损耗,主要是减少摩擦损耗。 2.效率以力或力矩的形式表达 如图910所示的传动装置,设F为驱动力,Q为生产阻力,和。分别为F和Q沿该力 作用线的速度,则由式(917)得 7=是=0。 (918)
203 A、B 处有机架 4 和连杆 2 对曲柄的总反力 R41 和 R21 。根据作用力与反作用力原理,即可确定 R21 的方向和位置。由于 R41 对中心 A 产生的摩擦力矩一定与曲柄相对机架的转动角速度方向相反, 可以确定 R41 位于摩擦圆的下方。根据曲柄上只受有两个总反力 R21 和 R41 和一个驱动力偶矩 M1, 因此,可知 R41 一定与 R21 平行、方向相反,组成一个阻力偶矩与驱动力偶矩 M1 平衡。从而可求 得 M1 的大小。 9.3 机械的效率和自锁 9.3.1 机械的效率及表达形式 1.效率以功或功率的形式表达 根据能量守恒定理,机械稳定运转时,输入功 Wd 等于输出功 Wr 和损耗功 Wf 之和,即 Wd = Wr +Wf (9-14) 通常,把机械的输出功 Wr 和输入功 Wd 的比值称为机械效率 ,即 r d f d =W /W =1−W /W (9-15) 它反映了输入功在机械中有效利用程度。 将式(9-14)的等号两端和式(9-15)的分子、分母各除以做功的时间 t,可得 Pd = Pr + Pf (9-16) 及 r d f d = P / P = 1− P / P (9-17) 式中, Pd 、 Pr 、 Pf 分别为输入功率、输出功率和损耗功率。 由于损耗功率不可能为零,所以机械的效率总是小于 1。为提高机械效率,应尽量减少机械 中的损耗,主要是减少摩擦损耗。 2.效率以力或力矩的形式表达 如图 9-10 所示的传动装置,设 F 为驱动力,Q 为生产阻力, F v 和 Q v 分别为 F 和 Q 沿该力 作用线的速度,则由式(9-17)得 F Q d r Fv Qv P P = = (9-18)
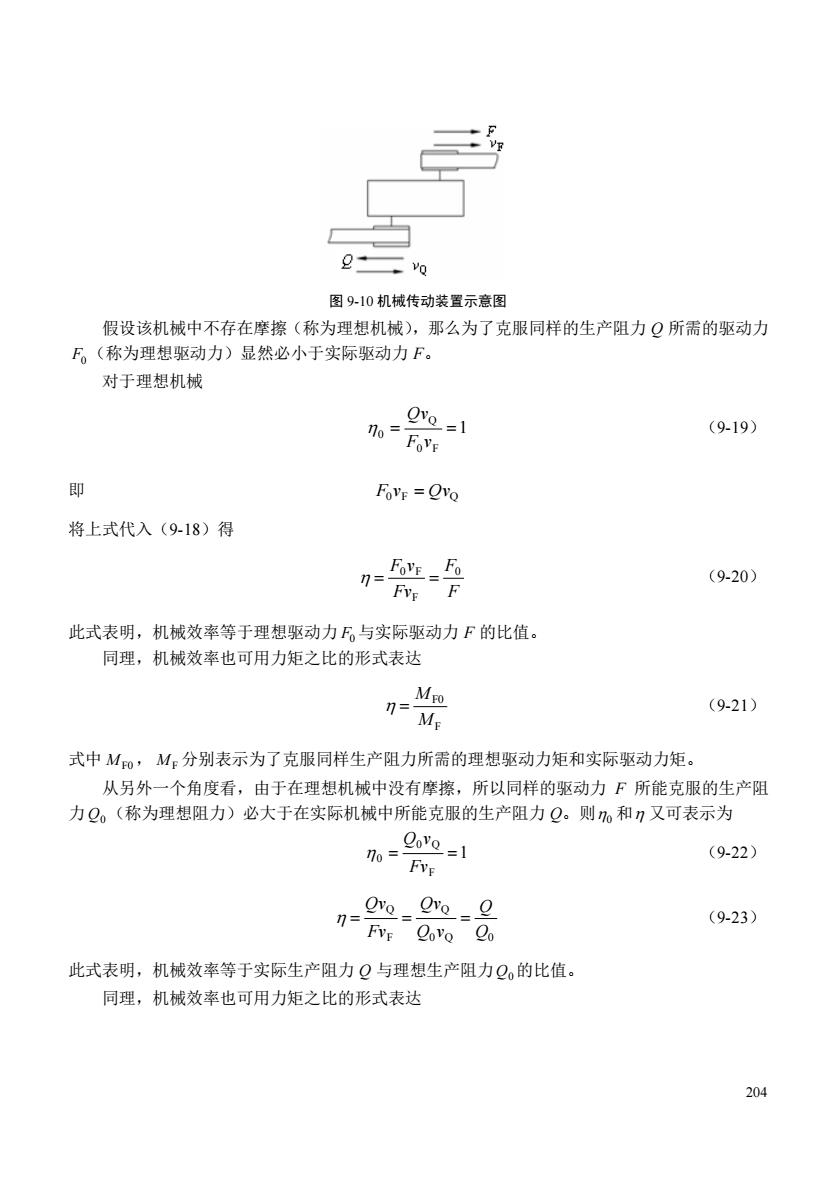
图910机械传动装置示意图 假设该机械中不存在摩擦(称为理想机械),那么为了克服同样的生产阻力Q所需的驱动力 厂。(称为理想驱动力)显然必小于实际驱动力F。 对于理想机械 Ovo=1 nloFoVr (9-19) 即 FOVE =Ovo 将上式代入(9-18)得 0号 (9-20) 此式表明,机械效率等于理想驱动力五与实际驱动力F的比值。 同理,机械效率也可用力矩之比的形式表达 M (9-21) 式中M,M,分别表示为了克服同样生产阻力所需的理想驱动力矩和实际驱动力矩。 从另外一个角度看,由于在理想机械中没有摩擦,所以同样的驱动力F所能克服的生产阻 力Q。(称为理想阻力)必大于在实际机械中所能克服的生产阻力Q。则%和n又可表示为 %-a0=1 (9-22) 7=9e=.g (9-23) FVF Covo Co 此式表明,机械效率等于实际生产阻力Q与理想生产阻力Q。的比值。 同理,机械效率也可用力矩之比的形式表达 204
204 图 9-10 机械传动装置示意图 假设该机械中不存在摩擦(称为理想机械),那么为了克服同样的生产阻力 Q 所需的驱动力 F0 (称为理想驱动力)显然必小于实际驱动力 F。 对于理想机械 1 0 F Q 0 = = F v Qv (9-19) 即 0 F QvQ F v = 将上式代入(9-18)得 F F Fv F v 0 F 0 F = = (9-20) 此式表明,机械效率等于理想驱动力 F0 与实际驱动力 F 的比值。 同理,机械效率也可用力矩之比的形式表达 F F0 M M = (9-21) 式中 M F0, M F 分别表示为了克服同样生产阻力所需的理想驱动力矩和实际驱动力矩。 从另外一个角度看,由于在理想机械中没有摩擦,所以同样的驱动力 F 所能克服的生产阻 力 Q0 (称为理想阻力)必大于在实际机械中所能克服的生产阻力 Q。则 0 和 又可表示为 1 F 0 Q 0 = = Fv Q v (9-22) 0 Q 0 Q F Q Q Q Q v Qv Fv Qv = = = (9-23) 此式表明,机械效率等于实际生产阻力 Q 与理想生产阻力 Q0 的比值。 同理,机械效率也可用力矩之比的形式表达

Mo (9-24) 式中,M。,M分别表示在同样驱动力情况下,机械所能克服的实际生产阻力矩和理想生产阻 力矩。 对于作变速运动的机械,在忽略动能变化的情况下,如用式(920)、(9-21)、(9-23)和(9-24) 计算机械效率,所得结果应为机械的瞬时效率。在一个运动循环内,不同时刻的瞬时效率是不同 的。用力或力矩之比来表达的瞬时效率,通常在对机构或机构系统进行效率分析时较为方便。 9.3.2机械系统的机械效率 上述讨论的是单个机构(或机器)的效率及计算,对于由许多机构(或机器)组成的机械系 统,机械效率的计算可以根据系统的组成情况和各个机构(或机器)的效率计算求得。常见简单 机构和运动副的效率如表91所示。若干机械的连接组合方式一般有串联、并联、混联三种,机 械系统的效率也相应的有三种不同的计算方法。 表91简单传动机构和运动副的效率 名称 传动形式 效率值 备注 67级精度齿轮传动 0.98-0.99 良好跑合、稀油润滑 8级精度齿轮传动 0.97 稀油润滑 圆柱齿轮传动 级精度齿轮传动 0.96 稀油润治 切制齿、开式齿轮传动 0.940.96 干油润滑 铸造齿、开式齿轮传动 0.900.93 67级精度齿轮传动 0.970.98 良好跑合、稀油润滑 8级精度齿轮传动 0.940.97 稀油润滑 锥齿轮传动 切制齿、开式齿轮传动 0.92-0.95 干油润滑 铸造齿、开式齿轮传动 0.88-0.92 白锁蜗杆 0.40-0.45 单头:蜗杆 0.70-0.75 蜗杆传动 双头蜗杆 0.750.82 润滑良好 三头和四头蜗杆 0.800.92 圆弧面蜗杆 0.85-0.95 平带传动 0.900.98 带传动 V形带传动 0.940.96 可步带传动 0.98-0.99 链传动 套筒滚子链 0.96 无声链 0.97 润滑良好 平摩擦轮传动 0.850.92 摩擦轮传动 槽摩擦轮传动 0.88-0.90 205
205 Q0 Q M M = (9-24) 式中, MQ,MQ0 分别表示在同样驱动力情况下,机械所能克服的实际生产阻力矩和理想生产阻 力矩。 对于作变速运动的机械,在忽略动能变化的情况下,如用式(9-20)、(9-21)、(9-23)和(9-24) 计算机械效率,所得结果应为机械的瞬时效率。在一个运动循环内,不同时刻的瞬时效率是不同 的。用力或力矩之比来表达的瞬时效率,通常在对机构或机构系统进行效率分析时较为方便。 9.3.2 机械系统的机械效率 上述讨论的是单个机构(或机器)的效率及计算,对于由许多机构(或机器)组成的机械系 统,机械效率的计算可以根据系统的组成情况和各个机构(或机器)的效率计算求得。常见简单 机构和运动副的效率如表 9-1 所示。若干机械的连接组合方式一般有串联、并联、混联三种,机 械系统的效率也相应的有三种不同的计算方法。 表 9-1 简单传动机构和运动副的效率 名称 传动形式 效率值 备注 圆柱齿轮传动 6~7级精度齿轮传动 0.98~0.99 良好跑合、稀油润滑 8级精度齿轮传动 0.97 稀油润滑 9级精度齿轮传动 0.96 稀油润滑 切制齿、开式齿轮传动 0.94~0.96 干油润滑 铸造齿、开式齿轮传动 0.90~0.93 锥齿轮传动 6~7级精度齿轮传动 0.97~0.98 良好跑合、稀油润滑 8级精度齿轮传动 0.94~0.97 稀油润滑 切制齿、开式齿轮传动 0.92~0.95 干油润滑 铸造齿、开式齿轮传动 0.88~0.92 蜗杆传动 自锁蜗杆 0.40~0.45 单头蜗杆 0.70~0.75 双头蜗杆 0.75~0.82 润滑良好 三头和四头蜗杆 0.80~0.92 圆弧面蜗杆 0.85~0.95 带传动 平带传动 0.90~0.98 V形带传动 0.94~0.96 同步带传动 0.98~0.99 链传动 套筒滚子链 0.96 润滑良好 无声链 0.97 摩擦轮传动 平摩擦轮传动 0.85~0.92 槽摩擦轮传动 0.88~0.90