
第五章凸轮机构 内容提要 本章首先介绍凸轮机构的组成、分类及应用,凸轮从动件常见的运动规律,其次重点介绍了 两种凸轮轮廓的设计方法,即作图法设计凸轮轮廓曲线和解析法设计凸轮轮廓曲线。 5.1概述 凸轮机构(cam mechanism)是最基本的高副机构,因为机构中有一特征构件一一凸轮,而 得名。凸轮机构可以通过设计合理的凸轮轮廓曲线,推动从动件精确地实现各种预期的运动规律, 还易于实现多个运动的相互协调配合。它广泛地应用于各种机械,特别是自动机械、自动控制装 置和装配生产线中。本章主要介绍凸轮机构的基本类型和特点、平面凸轮机构中高副的轮廓曲线 设计方法、平面凸轮机构基本尺寸的确定。 5.1.1凸轮机构的组成及应用 1.凸轮机构的组成 如图5-l、5-2所示的凸轮机构由凸轮(cam)、从动件(follower)和机架(house)所构成。 凸轮通常是具有曲线轮廓或凹槽的构件,当它运动时,通过力(常用弹簧)封闭或几何封闭使其 曲线轮廓与从动件形成高副接触,使从动件获得预期的运动。其最大优点是:只要设计出适当的 凸轮轮廓,就可以使从动件得到预期的运动规律,并且结构简单、紧凑、工作可靠,易于设计。 2.凸轮机构的应用 由于凸轮轮廓与从动件之间为高副接触,接触应力较大,易磨损,因此凸轮机构多用于传递 动力不大的场合。 凸轮机构主要应用于以下几方面: 1)实现运动与动力特性要求 如图5-1所示的内燃机气门控制机构,要求能在凸轮1高速转动的工况下,快速推动推杆2 (气阀)做有规律的往复运动,完成气门定时的开启、闭合动作,以控制燃气在适当的时间进入 气缸或排出废气。只要凸轮机构设计得当,就能够实现气阀的运动学要求,并且具有良好的动力 学性能
76 第五章 凸轮机构 内容提要 本章首先介绍凸轮机构的组成、分类及应用,凸轮从动件常见的运动规律,其次重点介绍了 两种凸轮轮廓的设计方法,即作图法设计凸轮轮廓曲线和解析法设计凸轮轮廓曲线。 5.1 概述 凸轮机构(cam mechanism)是最基本的高副机构,因为机构中有一特征构件——凸轮,而 得名。凸轮机构可以通过设计合理的凸轮轮廓曲线,推动从动件精确地实现各种预期的运动规律, 还易于实现多个运动的相互协调配合。它广泛地应用于各种机械,特别是自动机械、自动控制装 置和装配生产线中。本章主要介绍凸轮机构的基本类型和特点、平面凸轮机构中高副的轮廓曲线 设计方法、平面凸轮机构基本尺寸的确定。 5.1.1 凸轮机构的组成及应用 1.凸轮机构的组成 如图 5-1、5-2 所示的凸轮机构由凸轮(cam)、从动件(follower)和机架(house)所构成。 凸轮通常是具有曲线轮廓或凹槽的构件,当它运动时,通过力(常用弹簧)封闭或几何封闭使其 曲线轮廓与从动件形成高副接触,使从动件获得预期的运动。其最大优点是:只要设计出适当的 凸轮轮廓,就可以使从动件得到预期的运动规律,并且结构简单、紧凑、工作可靠,易于设计。 2.凸轮机构的应用 由于凸轮轮廓与从动件之间为高副接触,接触应力较大,易磨损,因此凸轮机构多用于传递 动力不大的场合。 凸轮机构主要应用于以下几方面: 1)实现运动与动力特性要求 如图 5-1 所示的内燃机气门控制机构,要求能在凸轮 1 高速转动的工况下,快速推动推杆 2 (气阀)做有规律的往复运动,完成气门定时的开启、闭合动作,以控制燃气在适当的时间进入 气缸或排出废气。只要凸轮机构设计得当,就能够实现气阀的运动学要求,并且具有良好的动力 学性能
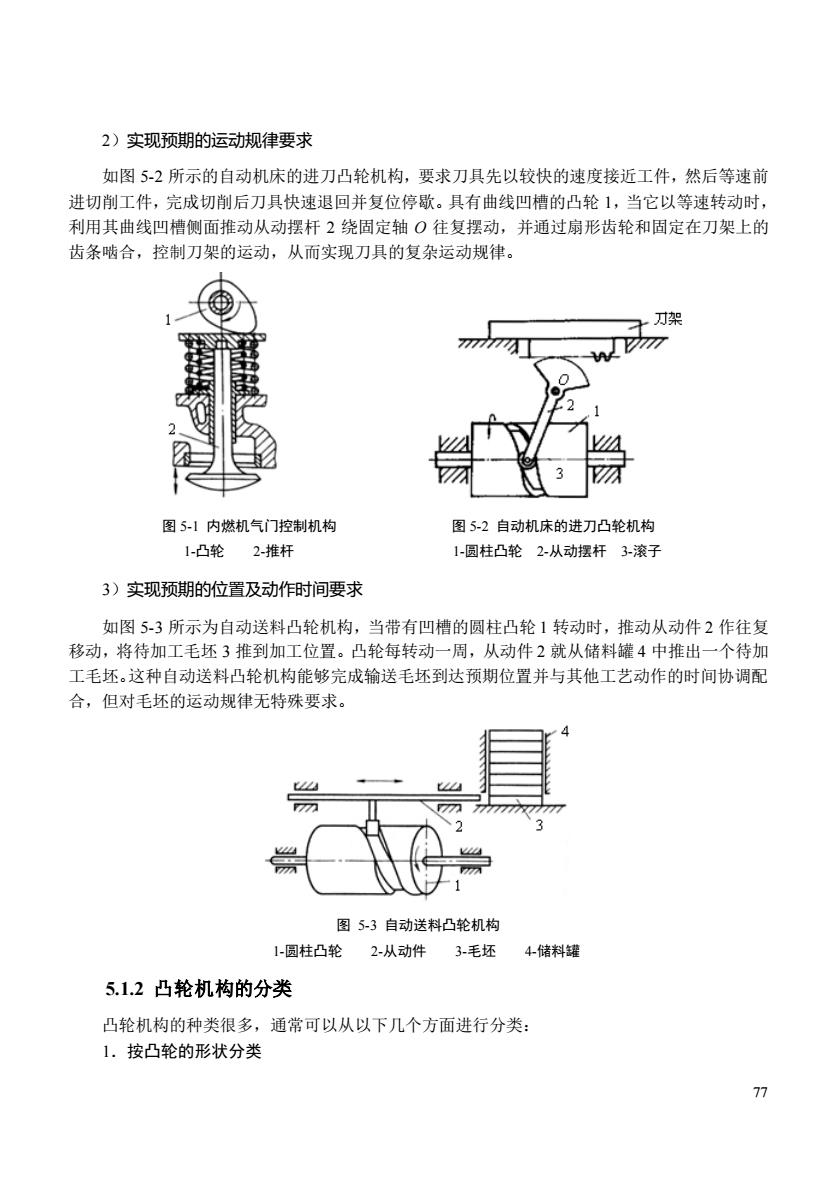
2)实现预期的运动规律要求 如图5-2所示的自动机床的进刀凸轮机构,要求刀具先以较快的速度接近工件,然后等速前 进切削工件,完成切削后刀具快速退回并复位停歇。具有曲线凹槽的凸轮1,当它以等速转动时, 利用其曲线凹槽侧面推动从动摆杆2绕固定轴O往复摆动,并通过扇形齿轮和固定在刀架上的 齿条啮合,控制刀架的运动,从而实现刀具的复杂运动规律。 ,架 777 图51内燃机气门控制机构 图52自动机床的进刀凸轮机构 1-凸轮2-推杆 1-圆柱凸轮2-从动摆杆3-滚子 3)实现预期的位置及动作时间要求 如图5-3所示为自动送料凸轮机构,当带有凹槽的圆柱凸轮1转动时,推动从动件2作往复 移动,将待加工毛坯3推到加工位置。凸轮每转动一周,从动件2就从储料罐4中推出一个待加 工毛坯。这种自动送料凸轮机构能够完成输送毛坯到达预期位置并与其他工艺动作的时间协调配 合,但对毛坯的运动规律无特殊要求。 图5-3自动送料凸轮机构 1-圆柱凸轮2-从动件3毛坯 4储料罐 5.1.2凸轮机构的分类 凸轮机构的种类很多,通常可以从以下几个方面进行分类: 1.按凸轮的形状分类
77 2)实现预期的运动规律要求 如图 5-2 所示的自动机床的进刀凸轮机构,要求刀具先以较快的速度接近工件,然后等速前 进切削工件,完成切削后刀具快速退回并复位停歇。具有曲线凹槽的凸轮 1,当它以等速转动时, 利用其曲线凹槽侧面推动从动摆杆 2 绕固定轴 O 往复摆动,并通过扇形齿轮和固定在刀架上的 齿条啮合,控制刀架的运动,从而实现刀具的复杂运动规律。 图 5-1 内燃机气门控制机构 图 5-2 自动机床的进刀凸轮机构 1-凸轮 2-推杆 1-圆柱凸轮 2-从动摆杆 3-滚子 3)实现预期的位置及动作时间要求 如图 5-3 所示为自动送料凸轮机构,当带有凹槽的圆柱凸轮 1 转动时,推动从动件 2 作往复 移动,将待加工毛坯 3 推到加工位置。凸轮每转动一周,从动件 2 就从储料罐 4 中推出一个待加 工毛坯。这种自动送料凸轮机构能够完成输送毛坯到达预期位置并与其他工艺动作的时间协调配 合,但对毛坯的运动规律无特殊要求。 图 5-3 自动送料凸轮机构 1-圆柱凸轮 2-从动件 3-毛坯 4-储料罐 5.1.2 凸轮机构的分类 凸轮机构的种类很多,通常可以从以下几个方面进行分类: 1.按凸轮的形状分类

I)盘形凸轮机构(plate cam mechanism) 在这种凸轮机构中,凸轮是一个绕定轴转动且具有变曲率半径的盘形构件,如图5-4a所示, 当凸轮绕定轴回转时,从动件在垂直于凸轮轴线的平面内运动,故又称为平面凸轮机构。它是最 基本的凸轮机构,应用最广。 2)移动凸轮机构(translating cam mechanism) 当盘形凸轮的回转中心趋于无穷远时,就演化为移动凸轮,如图5-4b所示。在移动凸轮机 构中,凸轮一般作往复直线运动。 3)圆柱凸轮机构(cylindrical cam mechanism) 在这种凸轮机构中,圆柱凸轮可以看成是将移动凸轮卷在圆柱体上而得到的凸轮,如图5-4c 所示。由于凸轮和从动件的运动平面不平行,因而这是一种空间凸轮机构。 (a (h) 图5-4按凸轮形状对凸轮机构分类 2.按从动件形状分类 I)尖顶从动件(knife-edge follower). 如图5-5a、b、f所示的凸轮机构中,从动件与凸轮的接触点为一尖点,称为尖顶。这种从 动件结构简单,尖顶能与任意复杂的凸轮轮廓保持接触,以实现从动件的任意运动规律。但尖顶 易于磨损,故只适用于传力不大的低速凸轮机构,如各种仪表机构等。 2)滚子从动件(roller follower) 如图5-5c、d、g所示的凸轮机构,从动件以铰接的滚子与凸轮轮廓接触。铰接的滚子与凸 轮轮廓间为滚动摩擦,不易磨损,可承受较大的载荷,因而应用最为广泛。 3)平底从动件(lat--faced follower) 如图5-5、h所示的凸轮机构中,从动件以平底与凸轮轮廓接触。它的优点是凸轮对从动件 的作用力方向始终与平底垂直,传动效率高,工作平稳,且平底与凸轮接触面间易形成油膜,利 于润滑,故常用于高速传动中。其缺点是不能与具有内凹轮廓的凸轮配对使用,也不能与移动凸 轮和圆柱凸轮配对使用。 3.按从动件运动形式分类
78 1)盘形凸轮机构(plate cam mechanism) 在这种凸轮机构中,凸轮是一个绕定轴转动且具有变曲率半径的盘形构件,如图 5-4a 所示。 当凸轮绕定轴回转时,从动件在垂直于凸轮轴线的平面内运动,故又称为平面凸轮机构。它是最 基本的凸轮机构,应用最广。 2)移动凸轮机构(translating cam mechanism) 当盘形凸轮的回转中心趋于无穷远时,就演化为移动凸轮,如图 5-4b 所示。在移动凸轮机 构中,凸轮一般作往复直线运动。 3)圆柱凸轮机构(cylindrical cam mechanism) 在这种凸轮机构中,圆柱凸轮可以看成是将移动凸轮卷在圆柱体上而得到的凸轮,如图 5-4c 所示。由于凸轮和从动件的运动平面不平行,因而这是一种空间凸轮机构。 (a) (b) (c) 图 5-4 按凸轮形状对凸轮机构分类 2.按从动件形状分类 1)尖顶从动件(knife-edge follower) 如图 5-5a、b、f 所示的凸轮机构中,从动件与凸轮的接触点为一尖点,称为尖顶。这种从 动件结构简单,尖顶能与任意复杂的凸轮轮廓保持接触,以实现从动件的任意运动规律。但尖顶 易于磨损,故只适用于传力不大的低速凸轮机构,如各种仪表机构等。 2)滚子从动件(roller follower) 如图 5-5c、d、g 所示的凸轮机构,从动件以铰接的滚子与凸轮轮廓接触。铰接的滚子与凸 轮轮廓间为滚动摩擦,不易磨损,可承受较大的载荷,因而应用最为广泛。 3)平底从动件(flat-faced follower) 如图 5-5e、h 所示的凸轮机构中,从动件以平底与凸轮轮廓接触。它的优点是凸轮对从动件 的作用力方向始终与平底垂直,传动效率高,工作平稳,且平底与凸轮接触面间易形成油膜,利 于润滑,故常用于高速传动中。其缺点是不能与具有内凹轮廓的凸轮配对使用,也不能与移动凸 轮和圆柱凸轮配对使用。 3.按从动件运动形式分类
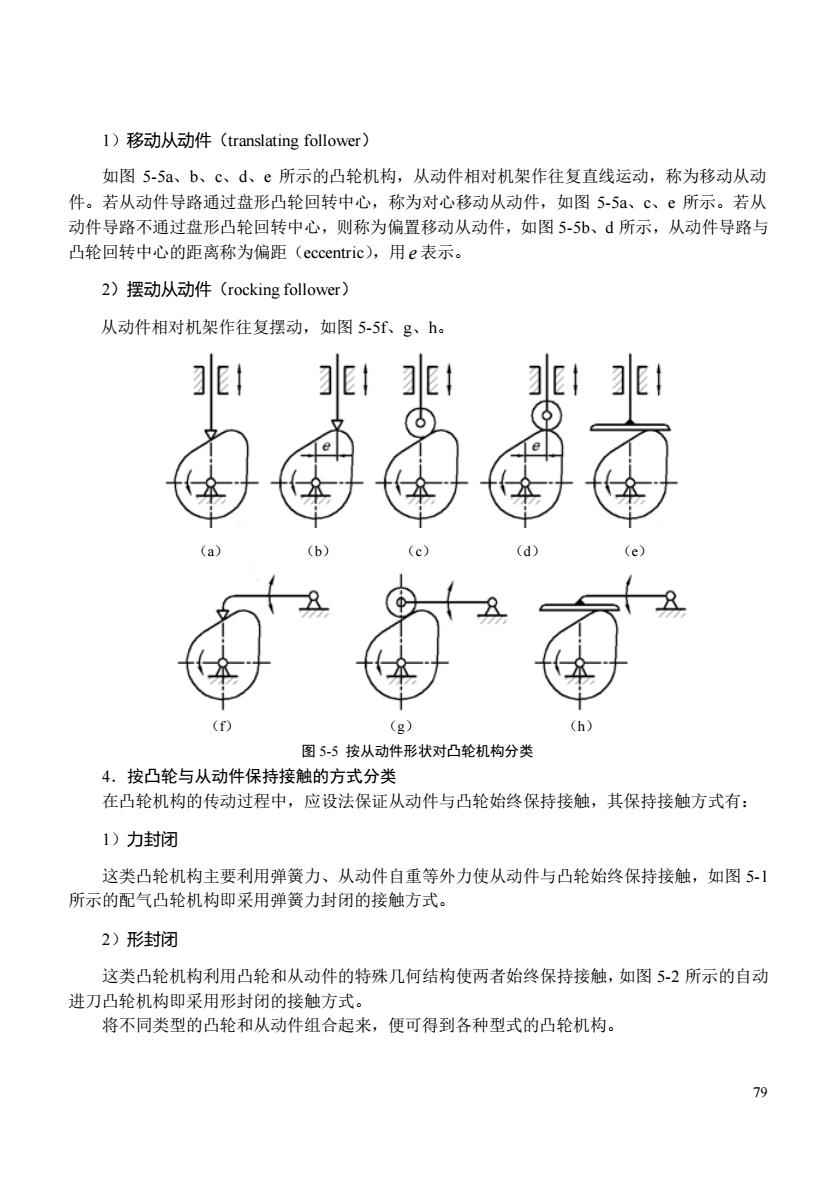
l)移动从动件(translating follower) 如图5-5a、b、c、d、c所示的凸轮机构,从动件相对机架作往复直线运动,称为移动从动 件。若从动件导路通过盘形凸轮回转中心,称为对心移动从动件,如图5-5、c、e所示。若从 动件导路不通过盘形凸轮回转中心,则称为偏置移动从动件,如图5-5b、d所示,从动件导路与 凸轮回转中心的距离称为偏距(eccentric),用e表示, 2)摆动从动件(rocking follower) 从动件相对机架作往复摆动,如图5-5f、g、h。 a d e (D (g) 图5-5按从动件形状对凸轮机构分类 4.按凸轮与从动件保持接触的方式分类 在凸轮机构的传动过程中,应设法保证从动件与凸轮始终保持接触,其保持接触方式有: 1)力封闭 这类凸轮机构主要利用弹簧力、从动件自重等外力使从动件与凸轮始终保持接触,如图5-」 所示的配气凸轮机构即采用弹簧力封闭的接触方式。 2)形封闭 这类凸轮机构利用凸轮和从动件的特殊几何结构使两者始终保持接触,如图5-2所示的自动 进刀凸轮机构即采用形封闭的接触方式。 将不同类型的凸轮和从动件组合起来,便可得到各种型式的凸轮机构
79 1)移动从动件(translating follower) 如图 5-5a、b、c、d、e 所示的凸轮机构,从动件相对机架作往复直线运动,称为移动从动 件。若从动件导路通过盘形凸轮回转中心,称为对心移动从动件,如图 5-5a、c、e 所示。若从 动件导路不通过盘形凸轮回转中心,则称为偏置移动从动件,如图 5-5b、d 所示,从动件导路与 凸轮回转中心的距离称为偏距(eccentric),用 e 表示。 2)摆动从动件(rocking follower) 从动件相对机架作往复摆动,如图 5-5f、g、h。 (a) (b) (c) (d) (e) (f) (g) (h) 图 5-5 按从动件形状对凸轮机构分类 4.按凸轮与从动件保持接触的方式分类 在凸轮机构的传动过程中,应设法保证从动件与凸轮始终保持接触,其保持接触方式有: 1)力封闭 这类凸轮机构主要利用弹簧力、从动件自重等外力使从动件与凸轮始终保持接触,如图 5-1 所示的配气凸轮机构即采用弹簧力封闭的接触方式。 2)形封闭 这类凸轮机构利用凸轮和从动件的特殊几何结构使两者始终保持接触,如图 5-2 所示的自动 进刀凸轮机构即采用形封闭的接触方式。 将不同类型的凸轮和从动件组合起来,便可得到各种型式的凸轮机构
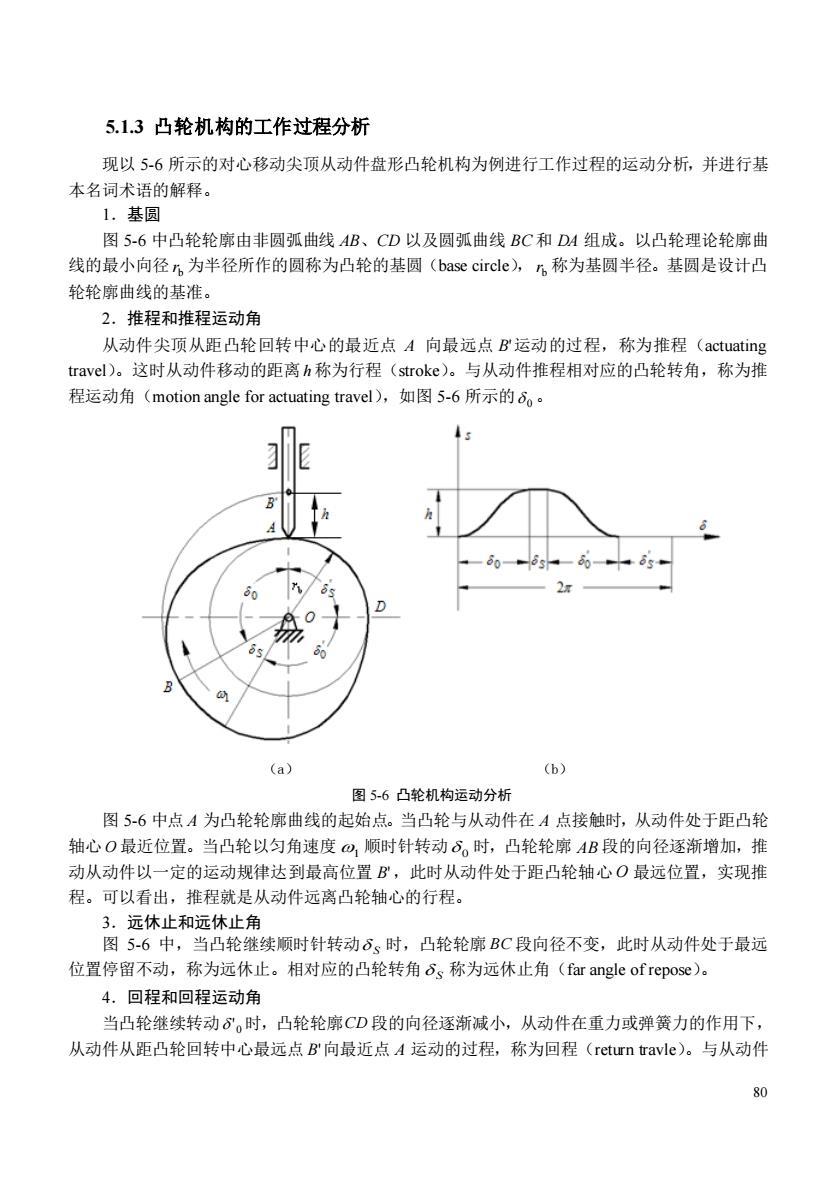
5.1.3凸轮机构的工作过程分析 现以5-6所示的对心移动尖顶从动件盘形凸轮机构为例进行工作过程的运动分析,并进行基 本名词术语的解释。 1.基圆 图5-6中凸轮轮廓由非圆弧曲线AB、CD以及圆弧曲线BC和DA组成。以凸轮理论轮廓曲 线的最小向径,为半径所作的圆称为凸轮的基圆(base circle,n称为基圆半径。基圆是设计凸 轮轮廓曲线的基准。 2.推程和推程运动角 从动件尖顶从距凸轮回转中心的最近点A向最远点B运动的过程,称为推程(actuating travel)。这时从动件移动的距离h称为行程(stroke)。与从动件推程相对应的凸轮转角,称为推 程运动角(motion angle for actuating travel),如图S-6所示的d。 (a) (b) 图5-6凸轮机构运动分析 图5-6中点A为凸轮轮廓曲线的起始点。当凸轮与从动件在A点接触时,从动件处于距凸轮 轴心O最近位置。当凸轮以匀角速度。顺时针转动6。时,凸轮轮廓AB段的向径逐渐增加,推 动从动件以一定的运动规律达到最高位置B,此时从动件处于距凸轮轴心O最远位置,实现推 程。可以看出,推程就是从动件远离凸轮轴心的行程。 3,远休止和元休止角 图5-6中,当凸轮继续顺时针转动6、时,凸轮轮廓BC段向径不变,此时从动件处于最远 位置停留不动,称为远休止。相对应的凸轮转角6s称为远休止角(far angle of repose)。 4.回程和回程运动角 当凸轮继续转动6”。时,凸轮轮廓CD段的向径逐渐减小,从动件在重力或弹簧力的作用下 从动件从距凸轮回转中心最远点B向最近点A运动的过程,称为回程(return travle)。与从动件
80 5.1.3 凸轮机构的工作过程分析 现以 5-6 所示的对心移动尖顶从动件盘形凸轮机构为例进行工作过程的运动分析,并进行基 本名词术语的解释。 1.基圆 图 5-6 中凸轮轮廓由非圆弧曲线 AB、CD 以及圆弧曲线 BC 和 DA 组成。以凸轮理论轮廓曲 线的最小向径 b r 为半径所作的圆称为凸轮的基圆(base circle), b r 称为基圆半径。基圆是设计凸 轮轮廓曲线的基准。 2.推程和推程运动角 从动件尖顶从距凸轮回转中心的最近点 A 向最远点 B' 运动的过程,称为推程(actuating travel)。这时从动件移动的距离 h 称为行程(stroke)。与从动件推程相对应的凸轮转角,称为推 程运动角(motion angle for actuating travel),如图 5-6 所示的 0 。 (a) (b) 图 5-6 凸轮机构运动分析 图 5-6 中点 A 为凸轮轮廓曲线的起始点。当凸轮与从动件在 A 点接触时,从动件处于距凸轮 轴心 O 最近位置。当凸轮以匀角速度 1 顺时针转动 0 时,凸轮轮廓 AB 段的向径逐渐增加,推 动从动件以一定的运动规律达到最高位置 B' ,此时从动件处于距凸轮轴心 O 最远位置,实现推 程。可以看出,推程就是从动件远离凸轮轴心的行程。 3.远休止和远休止角 图 5-6 中,当凸轮继续顺时针转动 S 时,凸轮轮廓 BC 段向径不变,此时从动件处于最远 位置停留不动,称为远休止。相对应的凸轮转角 S 称为远休止角(far angle of repose)。 4.回程和回程运动角 当凸轮继续转动 0 ' 时,凸轮轮廓 CD 段的向径逐渐减小,从动件在重力或弹簧力的作用下, 从动件从距凸轮回转中心最远点 B' 向最近点 A 运动的过程,称为回程(return travle)。与从动件

回程相对应的凸轮转角,称为回程运动角8。(motion angle for return travle)。可以看出,回程是 从动件移向凸轮轴心的行程。 5.近休止和近休止角 凸轮继续转动公时,凸轮轮廓DA段的向径不变,此时从动件在最近位置停留不动,称为 近休止,相应的凸轮转角云称为近休止角。 当凸轮再继续转动时,从动件重复上述运动循环。因凸轮作匀速转动,其转角6与时间1成 正比(6=),此时若以直角坐标系的纵坐标代表从动件位移s,横坐标代表凸轮的转角6, 则可画出从动件位移s与凸轮转角6之间的关系线图,如图5-6b所示,这种曲线则称为从动件 位移曲线,也可用它来描述从动件的运动规律。 从动件的运动规律是指其坛动参数(位移s、谏度和加谏度)随时间·变化的规律,常 用运动线图来表示。此时从动件的运动规律也可用从动件的运动参数随凸轮转角的变化规律来表 示,即s=s(6),v=v(6),a=a(6)。 由上述分析可知,从动件位移曲线取决于凸轮轮廓曲线的形状。反之,要设计凸轮的轮廓 曲线,则必须首先知道从动件的运动规律。 5.2从动件运动规律 5.2.1从动件常用运动规律 根据从动件运动规律所用数学表达式的不同,常用的主要有多项式运动规律和三角函数运动 规律两大类,下面分别加以介绍。 1.多项式运动规律 多项式函数具有高阶导数的连续性,因此在凸轮机构从动件运动规律的设计中得到了广泛的 应用。用多项式表示的从动件位移方程的一般形式为 s=Co+C6+C262+…+C.8m (5-1) 式中,6为凸轮转角:s为从动件位移:C。、C,、、C。分别为待定系数:n为多项式的次数。 可根据对从动件运动规律的具体要求,提出+1个边界条件代入上式,求出待定系数C。、C,、 C。,进而推导出多项式运动规律。 1)一次多项式运动规律(n=1) 设凸轮以等角速度o转动,凸轮的推程运动角为6。,从动件的行程为h,由式(5-1)可知, 一次多项式运动规律的表达式为 81
81 回程相对应的凸轮转角,称为回程运动角 0 ' (motion angle for return travle)。可以看出,回程是 从动件移向凸轮轴心的行程。 5.近休止和近休止角 凸轮继续转动 ' S 时,凸轮轮廓 DA 段的向径不变,此时从动件在最近位置停留不动,称为 近休止,相应的凸轮转角 ' S 称为近休止角。 当凸轮再继续转动时,从动件重复上述运动循环。因凸轮作匀速转动,其转角 与时间 t 成 正比( = t ),此时若以直角坐标系的纵坐标代表从动件位移 s,横坐标代表凸轮的转角 , 则可画出从动件位移 s 与凸轮转角 之间的关系线图,如图 5-6b 所示,这种曲线则称为从动件 位移曲线,也可用它来描述从动件的运动规律。 从动件的运动规律是指其运动参数(位移 s、速度 v 和加速度 a)随时间 t 变化的规律,常 用运动线图来表示。此时从动件的运动规律也可用从动件的运动参数随凸轮转角的变化规律来表 示,即 s = s( ) , v = v( ), a = a( )。 由上述分析可知,从动件位移曲线取决于凸轮轮廓曲线的形状。反之,要设计凸轮的轮廓 曲线,则必须首先知道从动件的运动规律。 5.2 从动件运动规律 5.2.1 从动件常用运动规律 根据从动件运动规律所用数学表达式的不同,常用的主要有多项式运动规律和三角函数运动 规律两大类,下面分别加以介绍。 1. 多项式运动规律 多项式函数具有高阶导数的连续性,因此在凸轮机构从动件运动规律的设计中得到了广泛的 应用。用多项式表示的从动件位移方程的一般形式为 n s C C C Cn 2 = 0 + 1 + 2 ++ (5-1) 式中, 为凸轮转角; s 为从动件位移; C0 、C1 、…、Cn 分别为待定系数; n 为多项式的次数。 可根据对从动件运动规律的具体要求,提出 n+1 个边界条件代入上式,求出待定系数 C0 、C1 、…、 Cn ,进而推导出多项式运动规律。 1)一次多项式运动规律( n =1 ) 设凸轮以等角速度 转动,凸轮的推程运动角为 0 ,从动件的行程为 h ,由式(5-1)可知, 一次多项式运动规律的表达式为

=Co+C6 Co (5-2) 假设边界条件为:在始点处,6=0,s=0:在终点处,6=6。,s=h。代入式(5-2)得C。=0, C=川6。,故从动件推程的运动方程为 V= ho (5-3) a=0 同理,根据回程时的边界条件:6=0,s=h:6=6。,s=0(其中6。为回程运动角)。代 入式(5-2)可得C。=h,C=-,故从动件回程的运动方程为 (5-4) a=0 注意:计算边界条件时,凸轮的转角6总是从该运动过程的起始位置起计量。 由于一次多项式函数的一阶导数为常数,所以此时从动件作匀速运动,故又称匀速运动规律 (constant velocity motion curve)。图5-7所示为其推程段的等速运动线图。由图可知,从动件在 运动开始和终止的瞬间,速度有突变,所以这时从动件在理论上将产生无穷大的加速度和惯性力, 因而会使凸轮机构受到极大的冲击。这种由于加速度无穷大而产生的冲击称为刚性冲击(gd impulse)。当然,由于实际凸轮机构中构件的弹性、阻尼等因素作用,惯性力不可能无穷大。因 此,等速运动规律通常只适用于低速轻载的场合,或对从动件有实现等速运动要求的场合,如图 5-2所示的自动机床的进刀凸轮机构。 2)二次多项式运动规律(n=2) 二次多项式的表达式为 82
82 = = = = = + 0 d d d d 1 0 1 t v a C t s v s C C (5-2) 假设边界条件为:在始点处, = 0 ,s = 0 ;在终点处, = 0 ,s = h 。代入式(5-2)得 C0 = 0 , 1 0 C = h ,故从动件推程的运动方程为 = = = 0 0 0 a h v h s (5-3) 同理,根据回程时的边界条件: = 0 , s = h ; ' = 0 ,s = 0 (其中 ' 0 为回程运动角)。代 入式(5-2)可得 C0 = h , ' C1 = −h 0 ,故从动件回程的运动方程为 = = − = − 0 1 ' 0 ' 0 a h v s h (5-4) 注意:计算边界条件时,凸轮的转角 总是从该运动过程的起始位置起计量。 由于一次多项式函数的一阶导数为常数,所以此时从动件作匀速运动,故又称匀速运动规律 (constant velocity motion curve)。图 5-7 所示为其推程段的等速运动线图。由图可知,从动件在 运动开始和终止的瞬间,速度有突变,所以这时从动件在理论上将产生无穷大的加速度和惯性力, 因而会使凸轮机构受到极大的冲击。这种由于加速度无穷大而产生的冲击称为刚性冲击(rigid impulse)。当然,由于实际凸轮机构中构件的弹性、阻尼等因素作用,惯性力不可能无穷大。因 此,等速运动规律通常只适用于低速轻载的场合,或对从动件有实现等速运动要求的场合,如图 5-2 所示的自动机床的进刀凸轮机构。 2)二次多项式运动规律( n = 2 ) 二次多项式的表达式为

s=C。+C6+C,62 v-ds-Co+2C.00 (5-5) d d业=2C20 由式(5-5)可知,这时从动件的加速度为常数。为了保证凸轮机构运动的平稳性,工程中 通常采用的二次多项式运动规律一般是:在一个运动行程中(推程或回程),前半段采用匀加速, 后半段采用匀减速,所以也称为匀加速匀减速运动规律(constant acceleration and deceleration motion curve)。这时,推程加速段的边界条件为:6=0,s=0,v=0:6=d。2,s=h/2。 将其代入式(5-5),可得C=0,C=0,C2=2h/,故从动件推程匀加速段的运动方程 s=2h82 (5-6) a=4ho? 式中6的变化范围为0~6/2 h/2 图57等速运动线图 图5-8等加速度等减速度速运动线图 由式(5-6)可知,在此阶段,从动件的位移5与凸轮转角6的平方成正比,故其位移曲线
83 = = = = + = + + 2 2 1 2 2 0 1 2 2 d d 2 d d C t v a C C t s v s C C C (5-5) 由式(5-5)可知,这时从动件的加速度为常数。为了保证凸轮机构运动的平稳性,工程中 通常采用的二次多项式运动规律一般是:在一个运动行程中(推程或回程),前半段采用匀加速, 后半段采用匀减速,所以也称为匀加速匀减速运动规律(constant acceleration and deceleration motion curve)。这时,推程加速段的边界条件为: = 0 , s = 0 ,v = 0 ; = 0 2 ,s = h 2 。 将其代入式(5-5),可得 C0 = 0 ,C1 = 0 , 2 C2 = 2h 0 ,故从动件推程匀加速段的运动方程 为 = = = 2 0 2 2 0 2 0 2 4 4 2 h a h v h s (5-6) 式中 的变化范围为 0 ~ 0 2 。 图 5-7 等速运动线图 图 5-8 等加速度等减速度速运动线图 由式(5-6)可知,在此阶段,从动件的位移 s 与凸轮转角 的平方成正比,故其位移曲线

为图5-10所示的一段向上凹的抛物线。 推程匀减速段的边界条件为:6=6/2,s=h2:6=d,s=h,v=0。将其代入式(S-5) 可得C=-h,G=4h/6。,C2=-2h。故从动件推程匀减速段的运动方程为 she (8-6) (5-7) 4ho? a=- 式中的变化范围为6.2~6。这时,从动件的位移曲线为图5-8所示的位移曲线上一段向下凹的 抛物线,两段反向抛物线在中点处光滑相连,故匀加速匀减速运动规律又称为抛物线运动规律 (parabolic motion curve). 由图5-8可知,加速度曲线上A、B、C三点的加速度为一有限值突变,因而引起的冲击 较小或较柔和,故称为柔性冲击(s0mpuc).。但在高速情况下仍将导致严重的振动、噪声和 磨损,所以这种运动规律只适用于中、低速轻载的工况。 同理,根据回程中的边界条件,可得回程时等加速等减速运动规律的运动方程为 回程匀加速段: s=h- 2h82 v-- 4ho8 05854 (5-8) as. 4ho? 回程匀减速段: 2h6- S= 6 V= -she (8,-6) (5-9) a= 3)五次多项式运动规律(n=5) 五次多项式的表达式为
84 为图 5-10 所示的一段向上凹的抛物线。 推程匀减速段的边界条件为: = 0 2 ,s = h 2 ; = 0 ,s = h ,v = 0 。将其代入式(5-5) 可得 C0 = −h , 1 0 C = 4h , 2 C2 = − 2h 0 。故从动件推程匀减速段的运动方程为 = − = − = − − 2 0 2 2 0 0 2 2 0 0 4 ( ) 4 ( ) 2 h a h v h s h (5-7) 式中的变化范围为 0 2 ~ 0 。这时,从动件的位移曲线为图 5-8 所示的位移曲线上一段向下凹的 抛物线,两段反向抛物线在中点处光滑相连,故匀加速匀减速运动规律又称为抛物线运动规律 (parabolic motion curve)。 由图 5-8 可知,加速度曲线上 A 、 B 、C 三点的加速度为一有限值突变,因而引起的冲击 较小或较柔和,故称为柔性冲击(soft impulse)。但在高速情况下仍将导致严重的振动、噪声和 磨损,所以这种运动规律只适用于中、低速轻载的工况。 同理,根据回程中的边界条件,可得回程时等加速等减速运动规律的运动方程为 回程匀加速段: = − = − = − 2 0 4 4 2 ' 0 2' 0 2 2' 0 2' 0 2 h a h v h s h (5-8) 回程匀减速段: = − − = = − ' 0 ' 0 2' 0 2 ' 2 0 ' 0 ' 2 2 0 ' 0 2 4 ( ) 4 ( ) 2 h a h v h s (5-9) 3)五次多项式运动规律( n = 5 ) 五次多项式的表达式为

s=C。+C6+C282+C63+C484+C,8 v=C0+2C200+3C3062+4C4063+5C,064 (5-10) a=+2C202+6C,026+12C40262+20C,028 因该方程组中待定系数有6个,故可设定6个边界条件为 在始点处:6=0,s=0,v=0,a=0。 在终点处:6=。,s=h,v=0,a=0。 代入式(5-10)可得C=0,C=0,C2=0,C=10h/,C4=15h/6,C=6h/。 由此可推出五次多项式运动规律的运动方程为 5=10h6_15h6+606 O0 s30 (5-11) a 60ho8-180ho282+120o2 式(5-11)的位移方程中分别含有3、4、5次幂,故这种运动规律又称为3-45次多项式。 图5-9所示为其运动线图,其中s为位移曲线,v为速度曲线,α为加速度曲线。由图可知,加 速度曲线光滑连续,故此运动规律既无刚性冲击也无柔性冲击,适于高速、中载的场合。 图5-9五次多项式运动线图 2.三角函数运动规律 三角函数运动规律包括简谐运动规律和摆线运动规律这两种基本的运动规律。 1)余弦加速度运动规律(cosine acceleration motion curve) 余弦加速度运动规律又称为简谐运动规律(simple harmonic motion curve),如图5-l0所示, 当质点沿着以推程为直径的圆周匀速运动时,它在直径上的投影点的运动即为简谐运动。其推 程的运动方程为
85 = + + + + = + + + + = + + + + + 2 3 5 2 2 4 2 3 2 2 4 5 3 4 2 1 2 3 5 5 4 4 3 3 2 0 1 2 2 6 12 20 2 3 4 5 a C C C C v C C C C C s C C C C C C (5-10) 因该方程组中待定系数有 6 个,故可设定 6 个边界条件为 在始点处: = 0 , s = 0 , v = 0 , a = 0 。 在终点处: = 0 , s = h , v = 0 , a = 0 。 代入式(5-10)可得 C0 = 0 ,C1 = 0 ,C2 = 0 , 3 C3 =10h 0 , 4 C4 = =15h 0 , 5 C5 = 6h 0 。 由此可推出五次多项式运动规律的运动方程为 = − + = − + = − + 2 3 5 0 2 2 4 0 2 3 0 4 5 0 3 4 0 2 3 0 5 5 0 4 4 0 3 3 0 60 180 120 30 60 30 10 15 6 h h h a h h h v h h h s (5-11) 式(5-11)的位移方程中分别含有 3、4、5 次幂,故这种运动规律又称为 3-4-5 次多项式。 图 5-9 所示为其运动线图,其中 s 为位移曲线,v 为速度曲线,a 为加速度曲线。由图可知,加 速度曲线光滑连续,故此运动规律既无刚性冲击也无柔性冲击,适于高速、中载的场合。 图 5-9 五次多项式运动线图 2.三角函数运动规律 三角函数运动规律包括简谐运动规律和摆线运动规律这两种基本的运动规律。 1)余弦加速度运动规律(cosine acceleration motion curve) 余弦加速度运动规律又称为简谐运动规律(simple harmonic motion curve),如图 5-10 所示, 当质点沿着以推程 h 为直径的圆周匀速运动时,它在直径上的投影点的运动即为简谐运动。其推 程的运动方程为