
第六章齿轮机构 内容提要 本章主要介绍齿轮机构的类型、特点及其应用:齿廓啮合的基本定律及渐开线齿廓的形成与 性质:渐开线标准直齿圆柱齿轮的基本参数与几何尺寸:渐开线齿廓的加工及变位齿轮与变位齿 轮传动:斜齿圆柱齿轮、圆锥齿轮与蜗杆传动机构,并简单介绍了其他类型的齿轮传动机构。重 点内容是齿轮的啮合原理与几何设计。 6.1概述 齿轮传动机构是机械传动中最主要、应用最为广泛的一种传动机构,可用来传递任意两轴之 间的运动和动力。 6.1.1齿轮传动的应用和特点 齿轮传动广泛地应用在工程机械、矿山机械、治金机械、各种机床及仪器、仪表工业等行业, 齿轮传动可用来传递回转运动,同时还可以用来转换直线与回转运动。与带传动、链传动等比较, 齿轮传动具有如下主要优点: (1)齿轮传动能保证瞬时传动比的恒定,传动平稳,传动比准确。 (2)结构紧凑、工作可靠、效率高、寿命长。 (3)传动的功率、速度和尺寸范围大。传递功率可以从不足一瓦至几十万千瓦:线速度可 达300ms:齿轮直径可以从几毫米至几十米。 齿轮传动也存在一些缺点,主要有:齿轮的齿数为整数,不能实现无级变速:啮合传动有一 定的噪声:需要有专门制造齿轮的设备,要求较高的制造和安装精度,加工成本高:中心距过大 时齿轮传动机构结构庞大、笨重,不适宜远距离传动。 6.1.2齿轮传动机构的类型 齿轮传动机构的类型很多,按照齿廓曲线的种类可分为:渐开线齿轮传动机构、摆线齿轮传 动机构和圆弧齿轮传动机构等。按照齿轮的形状,可分为:圆形齿轮传动机构和非圆形齿轮传动 机构。本章将讨论渐开线圆形齿轮传动机构。 在圆形齿轮机构中,根据两个传动轴线的相对位置可分为:平行轴齿轮传动机构、相交轴齿 106
106 第六章 齿轮机构 内容提要 本章主要介绍齿轮机构的类型、特点及其应用;齿廓啮合的基本定律及渐开线齿廓的形成与 性质;渐开线标准直齿圆柱齿轮的基本参数与几何尺寸;渐开线齿廓的加工及变位齿轮与变位齿 轮传动;斜齿圆柱齿轮、圆锥齿轮与蜗杆传动机构,并简单介绍了其他类型的齿轮传动机构。重 点内容是齿轮的啮合原理与几何设计。 6.1 概述 齿轮传动机构是机械传动中最主要、应用最为广泛的一种传动机构,可用来传递任意两轴之 间的运动和动力。 6.1.1 齿轮传动的应用和特点 齿轮传动广泛地应用在工程机械、矿山机械、冶金机械、各种机床及仪器、仪表工业等行业, 齿轮传动可用来传递回转运动,同时还可以用来转换直线与回转运动。与带传动、链传动等比较, 齿轮传动具有如下主要优点: (1)齿轮传动能保证瞬时传动比的恒定,传动平稳,传动比准确。 (2)结构紧凑、工作可靠、效率高、寿命长。 (3)传动的功率、速度和尺寸范围大。传递功率可以从不足一瓦至几十万千瓦;线速度可 达 300m/s;齿轮直径可以从几毫米至几十米。 齿轮传动也存在一些缺点,主要有:齿轮的齿数为整数,不能实现无级变速;啮合传动有一 定的噪声;需要有专门制造齿轮的设备,要求较高的制造和安装精度,加工成本高;中心距过大 时齿轮传动机构结构庞大、笨重,不适宜远距离传动。 6.1.2 齿轮传动机构的类型 齿轮传动机构的类型很多,按照齿廓曲线的种类可分为:渐开线齿轮传动机构、摆线齿轮传 动机构和圆弧齿轮传动机构等。按照齿轮的形状,可分为:圆形齿轮传动机构和非圆形齿轮传动 机构。本章将讨论渐开线圆形齿轮传动机构。 在圆形齿轮机构中,根据两个传动轴线的相对位置可分为:平行轴齿轮传动机构、相交轴齿

轮传动机构和交错轴齿轮传动机构 1,平行轴齿轮机构 两齿轮轴线相互平行的齿轮传动机构属于平面齿轮传动机构。常见的类型有直齿圆柱齿轮、 斜齿圆柱齿轮、人字齿轮传动和齿轮齿条传动。 1)直齿圆柱齿轮传动(spur gears) 直齿圆柱齿轮(spur gear)轮齿的方向与齿轮的轴线方向一致。当齿轮的轮齿在圆柱的外表 面上时称为外齿轮,如图6-1a中的两个齿轮和图6-b中的小齿轮:当轮齿在圆柱内表面上时称 为内齿轮,如图6-1b中的大齿轮。图6-1a所示的两个外齿轮啮合称为外啮合,外啮合传动时, 两齿轮转动方向相反:图61b所示的两一个内齿轮与一个外齿轮晒合时称为内啮合,内合传 动时,两齿轮的转动方向相同。直齿圆柱齿轮只能用于相互平行的两轴之间的传动。 2)斜齿圆柱齿轮传动(helical gears) 斜齿圆柱齿轮的轮齿方向与其轴线方向倾斜一个角度,这个角度称为螺旋角(helix angle)。 当两齿轮的螺旋角大小相同时,两齿轮轴线相互平行,称这种传动形式为斜齿轮传动。如图6-2 所示为外啮合斜齿圆柱齿轮传动(两齿轮螺旋角大小相同、方向相反);如图6-2b所示为内啮 合斜齿轮传动(两齿轮螺旋角大小与方向均相同)。 (a)外啮合 (b)内啮合 (a)外呐合 (b)内啮合 图61直齿圆柱齿轮传动 图6-2斜齿圆柱齿轮传动 3)人字齿轮传动(herringbone gears) 如图63错误:未找到引用源。所示的这种齿轮轮齿的方向呈人字形,可以看成是由两个螺 旋角大小相等、旋向相反的斜齿轮对称组合而成,故称为人字齿轮传动。 4)齿轮齿条传动(pinion and rack drive) 当齿轮的齿数趋于无穷多时,外齿轮就演变成齿条(ck),如图64所示。啮合时,齿轮转 动,齿条直线移动。 图6-3人字齿轮传动 图64齿轮齿条传动 2.相交轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线相交于一点,轴线交角通常为90°,如图65所示的圆锥齿 107
107 轮传动机构和交错轴齿轮传动机构。 1.平行轴齿轮机构 两齿轮轴线相互平行的齿轮传动机构属于平面齿轮传动机构。常见的类型有直齿圆柱齿轮、 斜齿圆柱齿轮、人字齿轮传动和齿轮齿条传动。 1)直齿圆柱齿轮传动(spur gears) 直齿圆柱齿轮(spur gear)轮齿的方向与齿轮的轴线方向一致。当齿轮的轮齿在圆柱的外表 面上时称为外齿轮,如图 6-1a 中的两个齿轮和图 6-1b 中的小齿轮;当轮齿在圆柱内表面上时称 为内齿轮,如图 6-1b 中的大齿轮。图 6-1a 所示的两个外齿轮啮合称为外啮合,外啮合传动时, 两齿轮转动方向相反;图 6-1b 所示的两一个内齿轮与一个外齿轮啮合时称为内啮合,内啮合传 动时,两齿轮的转动方向相同。直齿圆柱齿轮只能用于相互平行的两轴之间的传动。 2)斜齿圆柱齿轮传动(helical gears) 斜齿圆柱齿轮的轮齿方向与其轴线方向倾斜一个角度,这个角度称为螺旋角(helix angle)。 当两齿轮的螺旋角大小相同时,两齿轮轴线相互平行,称这种传动形式为斜齿轮传动。如图 6-2a 所示为外啮合斜齿圆柱齿轮传动(两齿轮螺旋角大小相同、方向相反);如图 6-2b 所示为内啮 合斜齿轮传动(两齿轮螺旋角大小与方向均相同)。 (a)外啮合 (b)内啮合 (a)外啮合 (b)内啮合 图 6-1 直齿圆柱齿轮传动 图 6-2 斜齿圆柱齿轮传动 3)人字齿轮传动(herringbone gears) 如图 6-3 错误!未找到引用源。所示的这种齿轮轮齿的方向呈人字形,可以看成是由两个螺 旋角大小相等、旋向相反的斜齿轮对称组合而成,故称为人字齿轮传动。 4)齿轮齿条传动(pinion and rack drive) 当齿轮的齿数趋于无穷多时,外齿轮就演变成齿条(rack),如图 6-4 所示。啮合时,齿轮转 动,齿条直线移动。 图 6-3 人字齿轮传动 图 6-4 齿轮齿条传动 2.相交轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线相交于一点,轴线交角通常为 90°,如图 6-5 所示的圆锥齿
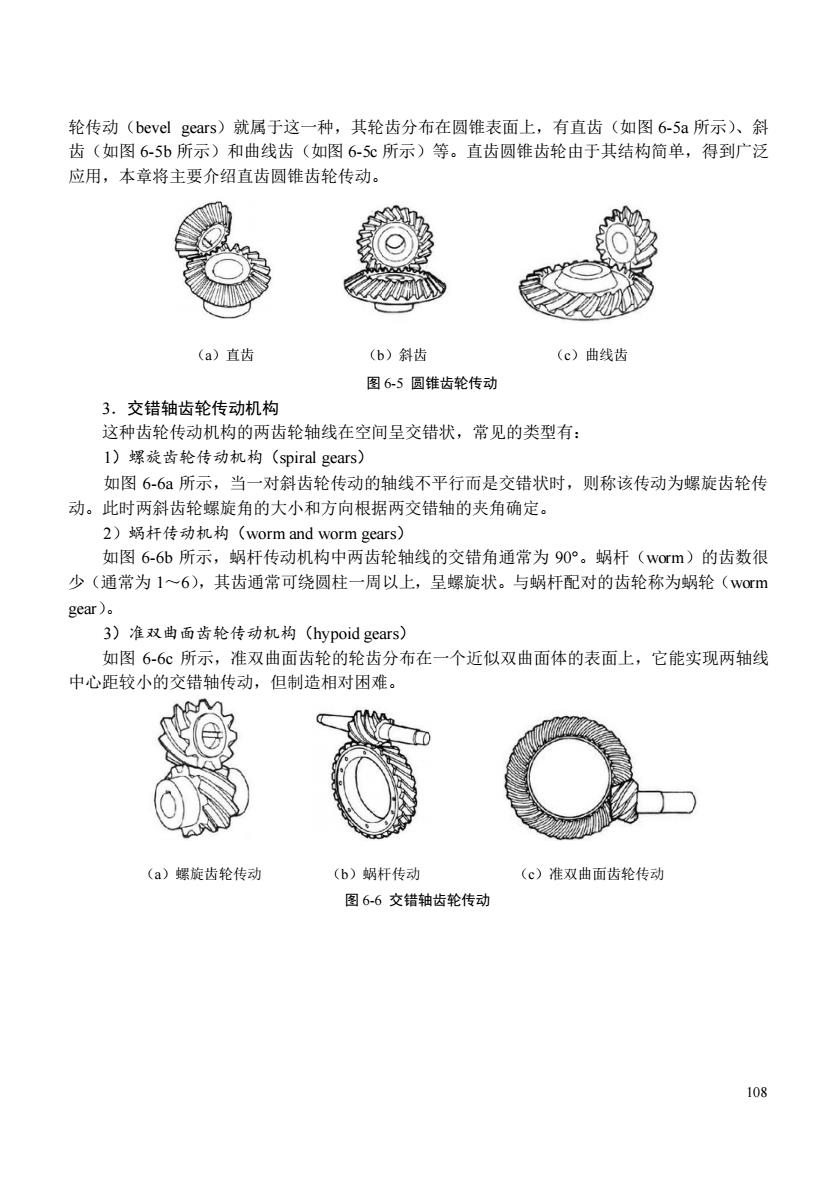
轮传动(bevel gears)就属于这一种,其轮齿分布在圆锥表面上,有直齿(如图6-5a所示)、斜 齿(如图6-5b所示)和曲线齿(如图65心所示)等。直齿圆锥齿轮由于其结构简单,得到广泛 应用,本章将主要介绍直齿圆锥齿轮传动。 (a)直齿 (b)斜齿 (c)曲线齿 图65圆锥齿轮传动 3.交错轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线在空间呈交错状,常见的类型有: 1)螺旋齿轮传动机构(spiral gears) 如图6-6a所示,当一对斜齿轮传动的轴线不平行而是交错状时,则称该传动为螺旋齿轮传 动。此时两斜齿轮螺旋角的大小和方向根据两交错轴的夹角确定。 2)蜗杆传动机构(worm and worm gears) 如图6-6b所示,蜗杆传动机构中两齿轮轴线的交错角通常为90°。蜗杆(wom)的齿数很 少(通常为1~6),其齿通常可绕圆柱一周以上,呈螺旋状。与蜗杆配对的齿轮称为蜗轮(w0m gea). 3)准双曲面齿轮传动机构(hypoid gears) 如图6-6c所示,准双曲面齿轮的轮齿分布在一个近似双曲面体的表面上,它能实现两轴线 中心距较小的交错轴传动,但制造相对困难。 (a)螺旋齿轮传动 (b)蜗杆传动 (c)准双曲面齿轮传动 图6-6交错轴齿轮传动 108
108 轮传动(bevel gears)就属于这一种,其轮齿分布在圆锥表面上,有直齿(如图 6-5a 所示)、斜 齿(如图 6-5b 所示)和曲线齿(如图 6-5c 所示)等。直齿圆锥齿轮由于其结构简单,得到广泛 应用,本章将主要介绍直齿圆锥齿轮传动。 (a)直齿 (b)斜齿 (c)曲线齿 图 6-5 圆锥齿轮传动 3.交错轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线在空间呈交错状,常见的类型有: 1)螺旋齿轮传动机构(spiral gears) 如图 6-6a 所示,当一对斜齿轮传动的轴线不平行而是交错状时,则称该传动为螺旋齿轮传 动。此时两斜齿轮螺旋角的大小和方向根据两交错轴的夹角确定。 2)蜗杆传动机构(worm and worm gears) 如图 6-6b 所示,蜗杆传动机构中两齿轮轴线的交错角通常为 90°。蜗杆(worm)的齿数很 少(通常为 1~6),其齿通常可绕圆柱一周以上,呈螺旋状。与蜗杆配对的齿轮称为蜗轮(worm gear)。 3)准双曲面齿轮传动机构(hypoid gears) 如图 6-6c 所示,准双曲面齿轮的轮齿分布在一个近似双曲面体的表面上,它能实现两轴线 中心距较小的交错轴传动,但制造相对困难。 (a)螺旋齿轮传动 (b)蜗杆传动 (c)准双曲面齿轮传动 图 6-6 交错轴齿轮传动

6.2齿廓啮合基本定律 齿轮传动是靠主动轮的齿廓依次推动从动轮的齿廓来实现的,齿廓曲线形状直接影响两齿轮 的瞬时传动比及轮齿的抗破坏能力,因此需要研究齿廊形状与齿轮机构传动之间的关系,即齿廓 啮合基本定律。 0所示为两齿廓啮合的情况,两齿廓在K点相切。过K点作两齿廓的公法线与两齿轮中 心连线O,O2相交于P点。由瞬心的概念可知,P点为两齿轮的瞬心,即 p1=p2=0O,P=0,O,P 若将一对相互啮合齿轮的转速(或角速度)之比称为传动比,则齿轮1与齿轮2的传动比 6÷兴器 (0-1) 图6-7中的P点称为两齿轮的啮合节点,简称节点(pitch point)。上式表明,一对齿轮在任 意位置啮合时的传动比,都与中心连线O,O,被节点P分成的两段长度成反比。这一规律称为齿 廓啮合的基本定律。 10 月=2 图6-7齿廓咕合基本定律 如果一对相互啮合齿轮的齿廓在不同的位置上啮合时,其节点P的位置是变化的,则两齿 轮的传动比就是变化的:若节点P的位置是固定的,则两个齿轮的传动比就是恒定的。齿轮传 动的最基本的要求是在啮合的过程中传动比保持恒定,满足这一要求的一对齿廓称为共轭齿廓。 理论上,只要给出两个齿轮的中心距、传动比和其中一个齿轮的齿廓曲线,就能求出组成一 对共轭齿廓的另一个齿轮的齿廓曲线。但考虑到设计、制造、安装和使用等因素,目前应用最多 的齿廓曲线是渐开线,其次是摆线,也有圆弧和抛物线等。 109
109 6.2 齿廓啮合基本定律 齿轮传动是靠主动轮的齿廓依次推动从动轮的齿廓来实现的,齿廓曲线形状直接影响两齿轮 的瞬时传动比及轮齿的抗破坏能力,因此需要研究齿廓形状与齿轮机构传动之间的关系,即齿廓 啮合基本定律。 0 所示为两齿廓啮合的情况,两齿廓在 K 点相切。过 K 点作两齿廓的公法线 n-n 与两齿轮中 心连线 O1O2 相交于 P 点。由瞬心的概念可知,P 点为两齿轮的瞬心,即 vP 1 = vP 2 =1O1P =2O2P 若将一对相互啮合齿轮的转速(或角速度)之比称为传动比,则齿轮 1 与齿轮 2 的传动比 O P O P n n i 1 2 2 1 2 1 12 = = = (0-1) 图 6-7 中的 P 点称为两齿轮的啮合节点,简称节点(pitch point)。上式表明,一对齿轮在任 意位置啮合时的传动比,都与中心连线 O1O2 被节点 P 分成的两段长度成反比。这一规律称为齿 廓啮合的基本定律。 图 6-7 齿廓啮合基本定律 如果一对相互啮合齿轮的齿廓在不同的位置上啮合时,其节点 P 的位置是变化的,则两齿 轮的传动比就是变化的;若节点 P 的位置是固定的,则两个齿轮的传动比就是恒定的。齿轮传 动的最基本的要求是在啮合的过程中传动比i保持恒定,满足这一要求的一对齿廓称为共轭齿廓。 理论上,只要给出两个齿轮的中心距、传动比和其中一个齿轮的齿廓曲线,就能求出组成一 对共轭齿廓的另一个齿轮的齿廓曲线。但考虑到设计、制造、安装和使用等因素,目前应用最多 的齿廓曲线是渐开线,其次是摆线,也有圆弧和抛物线等

6.3渐开线齿廓 6.3.1渐开线的形成与性质 如错误未找到引用源。所示,假想有一绳子缠绕在半径为,的圆周上,当从某一点A将绳 子拉离圆周表面时,其端点A的运动轨迹AK即称为该圆周的渐开线。该圆称为渐开线的基圆, 直线BK为渐开线的发生线,角日k称为AK段渐开线的展角 从渐开线的形成过程可知,渐开线具有以下性质: (I)发生线沿基圆滚过的长度BK等于基圆上被滚过的弧长AB,即BK=AB。 (2)渐开线上任意一点K的法线BK一定与其基圆相切。也就是说,切于基圆的直线必为 渐开线上某点的法线。 (3)发生线与基圆的切点B为渐开线在K点的曲率中心,而线段BK是渐开线在点K处的 曲率半径。渐开线越接近于基圆的部分,其曲率半径越小、曲率越大。渐开线起点A处的曲率 半径为零。 (4)渐开线的形状取决于基圆的大小。如图69所示,基圆越大,渐开线越平直:当基圆 半径趋于无穷大时,渐开线将变成一条直线,直线齿廓(如齿条)是渐开线齿廓的一种特例。 图6-8浙开线形成与特点 图69基圆与渐开线形状的关系 (5)基圆内无渐开线。 (6)齿廓上不同位置上的压力角不同。如图6-8所示,若以点0为齿轮的转动中心,AK 为齿廓曲线,F为作用于K点的正压力,Vx为K点的速度。根据压力角的定义,F与YK所夹的 锐角aK称为渐开线上任一点K的压力角。由图可知∠BOK=aK,所以 a=∠BOK=acos月 (0-2) 上式表明渐开线齿廓上各点的压力角是不同的。基圆上的压力角(α)为零,越远离基圆压 力角越大。 110
110 6.3 渐开线齿廓 6.3.1 渐开线的形成与性质 如错误!未找到引用源。所示,假想有一绳子缠绕在半径为 b r 的圆周上,当从某一点 A 将绳 子拉离圆周表面时,其端点 A 的运动轨迹 AK 即称为该圆周的渐开线。该圆称为渐开线的基圆, 直线 BK 为渐开线的发生线,角 K 称为 AK 段渐开线的展角。 从渐开线的形成过程可知,渐开线具有以下性质: (1)发生线沿基圆滚过的长度 BK 等于基圆上被滚过的弧长 AB ,即 BK = AB 。 (2)渐开线上任意一点 K 的法线 BK 一定与其基圆相切。也就是说,切于基圆的直线必为 渐开线上某点的法线。 (3)发生线与基圆的切点 B 为渐开线在 K 点的曲率中心,而线段 BK 是渐开线在点 K 处的 曲率半径。渐开线越接近于基圆的部分,其曲率半径越小、曲率越大。渐开线起点 A 处的曲率 半径为零。 (4)渐开线的形状取决于基圆的大小。如图 6-9 所示,基圆越大,渐开线越平直;当基圆 半径趋于无穷大时,渐开线将变成一条直线,直线齿廓(如齿条)是渐开线齿廓的一种特例。 图 6-8 渐开线形成与特点 图 6-9 基圆与渐开线形状的关系 (5)基圆内无渐开线。 (6)齿廓上不同位置上的压力角不同。如图 6-8 所示,若以点 O 为齿轮的转动中心,AK 为齿廓曲线,F 为作用于 K 点的正压力, K v 为 K 点的速度。根据压力角的定义,F 与 K v 所夹的 锐角 K 称为渐开线上任一点 K 的压力角。由图可知 BOK = K ,所以 K b K arccos r r = BOK = (0-2) 上式表明渐开线齿廓上各点的压力角是不同的。基圆上的压力角( b )为零,越远离基圆压 力角越大。 ) )

(7)同一基圆上任意两条渐开线之间的公法线长度处处相等。如图6-10所示的C和C·为 同一基圆上的两条反向渐开线,4B和4B,为C和C'之间的任意两条公法线,根据性质1和 2可知:4B=4B,=AB:同理,两条同向渐开线C和C"之间的任意两条公法线长度也相等, 即:BE=BE=BE。 图6-10同一基圆上任意两条渐开线之间的公法线长度处处相等 6.3.2渐开线方程 研究渐开线齿轮的啮合原理和几何尺寸计算时,常用到渐开线的方程,下面介绍极坐标形式 表示的渐开线方程。 根据渐开线的性质,在图6-8中,由△BOK的几何关系可知 Ik=CosCK (6-3) BK AB ri(0s +ax) tandx =OBOB Ov tan ay-a (6-4) 上式表明展角0k是压力角ak的函数,故称A是压力角ak的渐开线函数,工程上用vax 表示ak,即invak=Ak· 因此得渐开线的极坐标方程为 invak =0k tan ak -ak (0-5) 111
111 (7)同一基圆上任意两条渐开线之间的公法线长度处处相等。如图 6-10 所示的 C 和 C ' 为 同一基圆上的两条反向渐开线, A1B1 和 A2B2 为 C 和 C ' 之间的任意两条公法线,根据性质 1 和 2 可知: A1B1 = A2B2 = AB ;同理,两条同向渐开线 C ' 和 C " 之间的任意两条公法线长度也相等, 即: B1E1 = B2E2 = BE。 图 6-10 同一基圆上任意两条渐开线之间的公法线长度处处相等 6.3.2 渐开线方程 研究渐开线齿轮的啮合原理和几何尺寸计算时,常用到渐开线的方程,下面介绍极坐标形式 表示的渐开线方程。 根据渐开线的性质,在图 6-8 中,由 BOK 的几何关系可知 K b K cos r r = (6-3) ( ) b b K K K OB AB tan r r OB BK + = = = 即 K K K = tan − (6-4) 上式表明展角 K 是压力角 K 的函数,故称 K 是压力角 K 的渐开线函数,工程上用 K inv 表示 K ,即 K K inv = 。 因此得渐开线的极坐标方程为 K K K K b K K inv tan cos r r = = − = (0-5) ) ) )

6.4渐开线标准直齿圆柱齿轮的基本参数与几何尺寸 6.4.1齿轮各部分的名称 如错误:未找到引用源。所示为标准直齿外圆柱齿轮各部分的名称和符号 l.基圆(base circle)用于生成齿廓渐开线的圆,称为齿轮的基圆,其半径用n表示,直 径用d,表示。 2.齿顶圆(addendum circle)过齿轮齿顶端所作的圆,称为齿项圆,其半径用r,表示,直 径用d,表示。 3.齿根圆(dedendum circle)过轮齿槽底所作的圆,称为齿根圆,其半径用r,表示,直径 用dr表示。 4.分度圆(reference circle)为便于齿轮几何尺寸的表达和计算,在齿轮上规定一个圆作 为基准,将该圆称为分度圆,半径用r表示,直径用d表示。分度圆上具有标准的模数和压力角 (见后续章节介绍)。 5.齿顶高(addendum)分度圆和齿顶圆之间的部分称为齿顶,其径向距离称为齿顶高, 用h表示。 6.齿根高(dedendum)分度圆和齿根圆之间的部分称为齿根,其径向距离称为齿根高, 用h,表示。 7.全齿高齿顶圆和齿根圆之间的径向距离称为全齿高,用h表示,h=h,+: 8.齿厚(tooth thickness)沿任意圆周所量取的、轮齿两侧齿廓间的弧长,称为称为该圆周 上的齿厚,用5x表示。不同圆周上的齿厚是不同的,分度圆上的齿厚用s表示。 9.齿槽宽(space width)沿任意圆周所量取的、相邻两齿之间的弧长,称为该圆周上的齿 槽宽,用ex表示。不同圆周上的齿槽宽是不同的,分度圆上的齿槽宽用e表示。 l0.齿距(pit©h)在任意圆周上所量取的、相邻两齿同侧齿廓之间的弧长,称为该圆周上 的齿距,用Pk表示,Pk=5x+x。不同圆周上的齿距是不同的,分度圆上的齿距用p表示, p=s+e,且s=e:基圆的齿距用pb表示。 11.齿宽齿轮轮齿沿轴线方向的宽度称为齿宽,用B表示。 6.4.2齿轮的基本参数 齿轮的基本参数包括:齿轮的齿数:、模数m、齿顶高系数h、齿顶隙系数c和分度圆压力 角a,它们决定着齿轮的基本尺寸。 上资把地在合用p,.p: 可见计算得出的分度圆直径d与无理数π有关。为了便于计算、制造和检测,规定比值/π为 标准的数值,称作模数,用m表示,单位为毫米(mm),即m=P/π,由此可得分度圆齿距 112
112 6.4 渐开线标准直齿圆柱齿轮的基本参数与几何尺寸 6.4.1 齿轮各部分的名称 如错误!未找到引用源。所示为标准直齿外圆柱齿轮各部分的名称和符号。 1.基圆(base circle) 用于生成齿廓渐开线的圆,称为齿轮的基圆,其半径用 b r 表示,直 径用 b d 表示。 2.齿顶圆(addendum circle) 过齿轮齿顶端所作的圆,称为齿顶圆,其半径用 a r 表示,直 径用 a d 表示。 3.齿根圆(dedendum circle) 过轮齿槽底所作的圆,称为齿根圆,其半径用 f r 表示,直径 用 f d 表示。 4.分度圆(reference circle) 为便于齿轮几何尺寸的表达和计算,在齿轮上规定一个圆作 为基准,将该圆称为分度圆,半径用 r 表示,直径用 d 表示。分度圆上具有标准的模数和压力角 (见后续章节介绍)。 5.齿顶高(addendum) 分度圆和齿顶圆之间的部分称为齿顶,其径向距离称为齿顶高, 用 a h 表示。 6.齿根高(dedendum) 分度圆和齿根圆之间的部分称为齿根,其径向距离称为齿根高, 用 f h 表示。 7.全齿高 齿顶圆和齿根圆之间的径向距离称为全齿高,用 h 表示, h = ha + hf 。 8.齿厚(tooth thickness) 沿任意圆周所量取的、轮齿两侧齿廓间的弧长,称为称为该圆周 上的齿厚,用 K s 表示。不同圆周上的齿厚是不同的,分度圆上的齿厚用 s 表示。 9.齿槽宽(space width) 沿任意圆周所量取的、相邻两齿之间的弧长,称为该圆周上的齿 槽宽,用 K e 表示。不同圆周上的齿槽宽是不同的,分度圆上的齿槽宽用 e 表示。 10.齿距(pitch) 在任意圆周上所量取的、相邻两齿同侧齿廓之间的弧长,称为该圆周上 的齿距,用 K p 表示, K K K p = s + e 。不同圆周上的齿距是不同的,分度圆上的齿距用 p 表示, p = s + e ,且 s = e ;基圆的齿距用 pb 表示。 11.齿宽 齿轮轮齿沿轴线方向的宽度称为齿宽,用 B 表示。 6.4.2 齿轮的基本参数 齿轮的基本参数包括:齿轮的齿数 z、模数 m、齿顶高系数 * a h 、齿顶隙系数 * c 和分度圆压力 角 ,它们决定着齿轮的基本尺寸。 1.齿数(number of teeth) 齿轮在整个圆周上轮齿的总数,用 z 表示。 2.模数(module) 当已知齿轮齿数 z 和分度圆齿距 p 时,分度圆周长 d = zp ,即 d = zp / , 可见计算得出的分度圆直径 d 与无理数 有关。为了便于计算、制造和检测,规定比值 p / 为 一标准的数值,称作模数,用 m 表示,单位为毫米(mm),即 m = p / ,由此可得分度圆齿距

p=m (0-6) 因此,分度圆直径d为 d-周长=匹=严=忙 (0-7) 模数是齿轮计算中的基本参数,齿轮的模数越大,齿距与齿厚越大,相同齿数时分度圆直径 也越大。模数与齿厚及分度圆大小之间的关系见错误:未找到引用源。所示,图中三个齿轮的齿 数:相等。 =1 图611齿轮各部分名称和符号 图6-12不同模数的齿轮 为便于齿轮的设计和制造加工,齿轮的模数己经标准化,见表61。选用模数时,应优先选 用第一系列,其次是第二系列,而括号内的模数则尽可能不选用。 表6-1标准模数系列(GB1357-1987) (mm) 0.10.120.15020.250.50.40.50.60.811251.522.534 第一系列 5681012162025324050 第二系列 0.350.70.91.752.252.75(3.25)3.5(3.75)4.55.5(6.5)7 9(11)141822(30)36 45 3.压力角(pressure angle)通常将分度圆上的压力角称为齿轮压力角,用a表示。 因为齿轮在任意点啮合时COSaK=/,对于确定的齿轮,不变,随啮合点K点不同 而改变,所以不同点上啮合时压力角是不相等的。国标(GB1356-2001)规定分度圆上的压力角 α为标准值,一般情况下其值为20°。 4.齿顶高系数(coefficient of addendum)对于标准齿轮,其各部分尺寸都是用模数来表达 和计算的。国标规定齿轮的齿顶高 h=hm (6-8) 式中h称为齿顶高系数: 113
113 p =m (0-6) 因此,分度圆直径 d 为 mz pz mz d = = = = 周长 (0-7) 模数是齿轮计算中的基本参数,齿轮的模数越大,齿距与齿厚越大,相同齿数时分度圆直径 也越大。模数与齿厚及分度圆大小之间的关系见错误!未找到引用源。所示,图中三个齿轮的齿 数 z 相等。 图 6-11 齿轮各部分名称和符号 图 6-12 不同模数的齿轮 为便于齿轮的设计和制造加工,齿轮的模数已经标准化,见表 6-1。选用模数时,应优先选 用第一系列,其次是第二系列,而括号内的模数则尽可能不选用。 表 6-1 标准模数系列(GB1357-1987) (mm) 第一系列 0.1 0.12 0.15 0.2 0.25 0.5 0.4 0.5 0.6 0.8 1 1.25 1.5 2 2.5 3 4 5 6 8 10 12 16 20 25 32 40 50 第二系列 0.35 0.7 0.9 1.75 2.25 2.75 (3.25) 3.5 (3.75) 4.5 5.5 (6.5) 7 9 (11) 14 18 22 (30) 36 45 3.压力角(pressure angle) 通常将分度圆上的压力角称为齿轮压力角,用 表示。 因为齿轮在任意点啮合时 K b K cos = r / r ,对于确定的齿轮, b r 不变, K r 随啮合点 K 点不同 而改变,所以不同点上啮合时压力角是不相等的。国标(GB1356-2001)规定分度圆上的压力角 为标准值,一般情况下其值为 20º。 4.齿顶高系数(coefficient of addendum) 对于标准齿轮,其各部分尺寸都是用模数来表达 和计算的。国标规定齿轮的齿顶高 h h m * a = a (6-8) 式中 * a h 称为齿顶高系数

5.顶隙系数(coefficient of addendum)两齿轮在啮合传动时,一个齿轮的齿顶圆与另一个 齿轮的齿根圆之间要留有一定的间隙,此间隙的径向高度称为顶隙(bottom clearance),用c表 示。标准顶隙也是模数m的倍数,表示为 c=c'm (6-9) 式中c'称为顶隙系数。 渐开线标准直齿圆柱齿轮的基本参数均为标准值,其中齿顶高系数和顶隙系数¢'也己标 准化,对于正常齿制的齿轮:=1,c=0.25:短齿制的齿轮:=0.8,c=0.3。 6.4.3浙开线标准直齿圆柱齿轮几何尺寸的计算 m、a、h和c'均为标准值,且s=e的齿轮,称为标准齿轮。表6-2所示为外啮合渐开线 标准直齿圆柱齿轮几何尺寸的计算公式。 表62渐开线标准直齿圆柱齿轮几何尺寸计算公式 名称 符号 小齿轮 大齿轮 齿数 , 分度圆直径 d d1=m1 d=2 齿项高 h.=h.m 齿根高 h 4=(6+cm 齿全高 h h=h+h 齿顶圆直径 da da=di+2h d2=d2+2h 齿根圆直径 d dn=d-2h d2=d2-2h 基圆直径 do=d cosa die=d cosa 齿距 D D=刀 齿宽 s=p/2 齿槽宽 e e=p/2 基圆齿距 A P=pcosa 法向齿距 任意圆上的压力角 0osax=片/r 任意圆上的齿厚 0 k-s-2(mak-ima),其中mak=&=tandk-ak 标准中心距 0 a=(d+d2) 传动比 公品异 1.基圆齿距 任一圆周上的齿距都等于其圆周长与齿轮齿数的比值,即PK-2,所以,-2红5 114
114 5.顶隙系数(coefficient of addendum) 两齿轮在啮合传动时,一个齿轮的齿顶圆与另一个 齿轮的齿根圆之间要留有一定的间隙,此间隙的径向高度称为顶隙(bottom clearance),用 c 表 示。标准顶隙也是模数 m 的倍数,表示为 c c m * = (6-9) 式中 * c 称为顶隙系数。 渐开线标准直齿圆柱齿轮的基本参数均为标准值,其中齿顶高系数 * a h 和顶隙系数 * c 也已标 准化,对于正常齿制的齿轮: 1 * ha = , 0.25 * c = ;短齿制的齿轮: 0.8 * ha = , 0.3 * c = 。 6.4.3 渐开线标准直齿圆柱齿轮几何尺寸的计算 m、 、 * a h 和 * c 均为标准值,且 s = e 的齿轮,称为标准齿轮。表 6-2 所示为外啮合渐开线 标准直齿圆柱齿轮几何尺寸的计算公式。 表 6-2 渐开线标准直齿圆柱齿轮几何尺寸计算公式 名称 符号 小齿轮 大齿轮 齿数 z 1 z 2 z 分度圆直径 d d1 = mz1 d2 = mz2 齿顶高 a h h h m * a = a 齿根高 f h h (h c )m * f a = + 齿全高 h h = ha + hf 齿顶圆直径 a d da1 = d1 + 2ha da2 = d2 + 2ha 齿根圆直径 f d df1 = d1 − 2hf df2 = d2 − 2hf 基圆直径 b d db1 = d1 cos db2 = d2 cos 齿距 p p = m 齿宽 s s = p / 2 齿槽宽 e e = p / 2 基圆齿距 b p pb = pcos 法向齿距 n p pn = pb 任意圆上的压力角 K K b K cos = r /r 任意圆上的齿厚 K s 2 ( ) K K K K r inv inv r r s = s − − ,其中 K K K K inv = = tan − 标准中心距 a ( ) 2 1 a = d1 + d2 传动比 12 i 1 2 2 1 2 1 12 z z n n i = = = 1.基圆齿距 任一圆周上的齿距都等于其圆周长与齿轮齿数的比值,即 z r p K K 2 = ,所以 z r p b b 2 =

将=心osa代入即得 -2rc0g=代0a (0-10) 2.法向齿距 在齿廓的法线方向上测得的相邻两同向齿廓间的距离,称为法向齿距,用P。表示 如错误未找到引用源。所示,在基圆上任选一点N,作基圆的切线NB,由渐开线的性质可 知,该线是渐开线4B,和42B2所在齿廓的公法线,则将B,B,称为两轮齿的法向齿距。 因为NB=⑦,NB,=,所以 P,=BB,=NB,-N8=4,-=4A,=p (6-11) 可见法向齿距与切点N的选择无关,与基圆齿距相等。 3.任意圆上的齿厚 齿轮在不同圆周上的齿厚是不同的,如图6-14所示为齿轮的一个轮齿,其中人、s、α、日分 别表示齿轮分度圆半径、齿厚、压力角及渐开线展角:k、5K、k及0k分别表示齿轮任意圆 上的半径、齿厚、压力角及展角:为任意圆上齿厚所对应的圆心角。 由图可知 s=kp=rk(∠COC-2∠C'O) 将∠C0C'=三、∠COK=Ax-0、mvax=&代入可得 k=[月-2avas-va]--2a-va (6-12) 图613法向齿距与基圆齿距相等 图614任意圆齿厚 115
115 将 rb = rcos 代入即得 cos 2 cos b p z r p = = (0-10) 2.法向齿距 在齿廓的法线方向上测得的相邻两同向齿廓间的距离,称为法向齿距,用 pn 表示。 如错误!未找到引用源。所示,在基圆上任选一点 N,作基圆的切线 NB ,由渐开线的性质可 知,该线是渐开线 A1B1 和 A2B2 所在齿廓的公法线,则将 B1B2 称为两轮齿的法向齿距。 因为 NB1 = NA1 , NB2 = NA2 ,所以 pn = B1B2 = NB2 − NB1 = NA2 − NA1 = A1A2 = pb (6-11) 可见法向齿距与切点 N 的选择无关,与基圆齿距相等。 3.任意圆上的齿厚 齿轮在不同圆周上的齿厚是不同的,如图 6-14 所示为齿轮的一个轮齿,其中 r、s、 、 分 别表示齿轮分度圆半径、齿厚、压力角及渐开线展角; K r 、 K s 、 K 及 K 分别表示齿轮任意圆 上的半径、齿厚、压力角及展角; 为任意圆上齿厚所对应的圆心角。 由图可知 sK = rK = rK(COC '−2C 'OK') 将 r s COC ' = 、 C 'OK' = K − 、 K K inv = 代入可得 2(inv inv ) 2 (inv inv ) K K K K K K = − − = − − r r r s r s s r (6-12) 图 6-13 法向齿距与基圆齿距相等 图 6-14 任意圆齿厚 ) ) ) ) )