
第七章轮系 内容提要 本章简要介绍了轮系的功用和分类,重点介绍定轴轮系、周转轮系和复合轮系的传动比计算, 并介绍了行星轮系的设计,最后简单介绍了其他常见行星轮系机构。 7.1概述 就传动而言,齿轮机构无疑是现代机械中最重要的一种传动装置,但在实际机械中,为了满 足不同的工作需要,仅用一对齿轮组成的齿轮机构往往是不够的。因此常常需要采用由一系列互 相啮合的齿轮组成的传动系统来满足不同的工作需要,这种由一系列的齿轮所组成的齿轮传动系 统称为齿轮系,简称轮系(gear train)。 7.1.1轮系的功用 轮系在机械传动中应用非常广泛,可以用以实现分路传动、换向传动、变速传动、大传动 比传动及运动的合成与分解等。 如图7-1a所示为某航空发动机附件传动系统,通过轮系将主轴的运动分成六路传出,带动 各附件同时工作。 如图71b所示为车床上走刀丝杠的三星轮换向机构,在主动轮1转向不变的条件下,通过 改变手柄的位置,使齿轮2参与啮合或不参与啮合,以改变外啮合的次数,使从动轮4与主动轮 1转向相反或相同。 如图7-1℃所示,利用双联齿轮的滑移使主动轴转速不变的情况下,从动轴可获得两种不同 的转速。 如图7-1所示,如果仅采用一对齿轮传动(如图虚线所示),必然会使两齿轮的尺寸相差 很大,这样不仅会使传动机构尺寸庞大,而且因小齿轮工作次数过多容易失效,所以一般情况下 一对齿轮传动的传动比要求i≤8。而由图中实线可知,传动同样距离、同样大小的传动比,若 采用轮系,则各齿轮尺寸明显减小,结构也更紧凑。 如图7-1©所示,当以齿轮1和齿轮3为原动机,并且齿数满足某种关系时,则构件H的转 速是齿轮1、3转速的合成。这种特性在机床、计算机装置及补偿装置中具有广泛的应用。而在 汽车后桥差速器中确利用它作为运动分解装置,它将发动机传递过来的运动,通过构件H分解 为与左右车轮固联的齿轮1、3的独立运动。 155
155 第七章 轮系 内容提要 本章简要介绍了轮系的功用和分类,重点介绍定轴轮系、周转轮系和复合轮系的传动比计算, 并介绍了行星轮系的设计,最后简单介绍了其他常见行星轮系机构。 7.1 概述 就传动而言,齿轮机构无疑是现代机械中最重要的一种传动装置,但在实际机械中,为了满 足不同的工作需要,仅用一对齿轮组成的齿轮机构往往是不够的。因此常常需要采用由一系列互 相啮合的齿轮组成的传动系统来满足不同的工作需要,这种由一系列的齿轮所组成的齿轮传动系 统称为齿轮系,简称轮系(gear train)。 7.1.1 轮系的功用 轮系在机械传动中应用非常广泛,可以用以实现分路传动、换向传动、变速传动、大传动 比传动及运动的合成与分解等。 如图 7-1a 所示为某航空发动机附件传动系统,通过轮系将主轴的运动分成六路传出,带动 各附件同时工作。 如图 7-1b 所示为车床上走刀丝杠的三星轮换向机构,在主动轮 1 转向不变的条件下,通过 改变手柄的位置,使齿轮 2 参与啮合或不参与啮合,以改变外啮合的次数,使从动轮 4 与主动轮 1 转向相反或相同。 如图 7-1c 所示,利用双联齿轮的滑移使主动轴转速不变的情况下,从动轴可获得两种不同 的转速。 如图 7-1d 所示,如果仅采用一对齿轮传动(如图虚线所示),必然会使两齿轮的尺寸相差 很大,这样不仅会使传动机构尺寸庞大,而且因小齿轮工作次数过多容易失效,所以一般情况下 一对齿轮传动的传动比要求 i 8 。而由图中实线可知,传动同样距离、同样大小的传动比,若 采用轮系,则各齿轮尺寸明显减小,结构也更紧凑。 如图 7-1e 所示,当以齿轮 1 和齿轮 3 为原动机,并且齿数满足某种关系时,则构件 H 的转 速是齿轮 1、3 转速的合成。这种特性在机床、计算机装置及补偿装置中具有广泛的应用。而在 汽车后桥差速器中确利用它作为运动分解装置,它将发动机传递过来的运动,通过构件 H 分解 为与左右车轮固联的齿轮 1、3 的独立运动
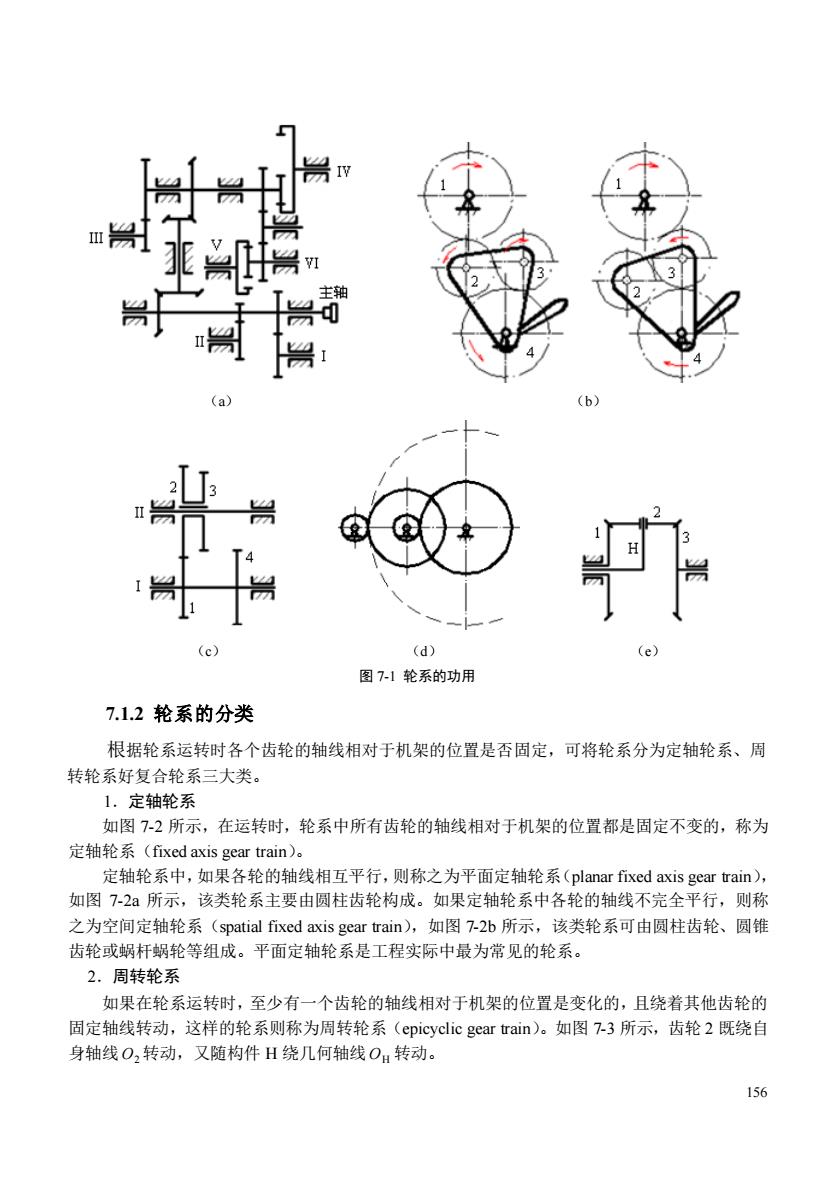
(d) (c】 图7-1轮系的功用 7.1.2轮系的分类 根据轮系运转时各个齿轮的轴线相对于机架的位置是否固定,可将轮系分为定轴轮系、周 转轮系好复合轮系三大类。 1.定轴轮系 如图7-2所示,在运转时,轮系中所有齿轮的轴线相对于机架的位置都是固定不变的,称为 定轴轮系((fixed axis gear train)。 定轴轮系中,如果各轮的轴线相互平行,则称之为平面定轴轮系(planar fixed axis gear train)。 如图7-2所示,该类轮系主要由圆柱齿轮构成。如果定轴轮系中各轮的轴线不完全平行,则称 之为空间定轴轮系(spatial fixed axis gear train),如图7-2b所示,该类轮系可由圆柱齿轮、圆锥 齿轮或蜗杆蜗轮等组成。平面定轴轮系是工程实际中最为常见的轮系。 2.周转轮系 如果在轮系运转时,至少有一个齿轮的轴线相对于机架的位置是变化的,且绕着其他齿轮的 固定轴线转动,这样的轮系则称为周转轮系(epicyclic gear train)。如图7-3所示,齿轮2既绕自 身轴线O2转动,又随构件H绕几何轴线O:转动。 156
156 (a) (b) (c) (d) (e) 图 7-1 轮系的功用 7.1.2 轮系的分类 根据轮系运转时各个齿轮的轴线相对于机架的位置是否固定,可将轮系分为定轴轮系、周 转轮系好复合轮系三大类。 1.定轴轮系 如图 7-2 所示,在运转时,轮系中所有齿轮的轴线相对于机架的位置都是固定不变的,称为 定轴轮系(fixed axis gear train)。 定轴轮系中,如果各轮的轴线相互平行,则称之为平面定轴轮系(planar fixed axis gear train), 如图 7-2a 所示,该类轮系主要由圆柱齿轮构成。如果定轴轮系中各轮的轴线不完全平行,则称 之为空间定轴轮系(spatial fixed axis gear train),如图 7-2b 所示,该类轮系可由圆柱齿轮、圆锥 齿轮或蜗杆蜗轮等组成。平面定轴轮系是工程实际中最为常见的轮系。 2.周转轮系 如果在轮系运转时,至少有一个齿轮的轴线相对于机架的位置是变化的,且绕着其他齿轮的 固定轴线转动,这样的轮系则称为周转轮系(epicyclic gear train)。如图 7-3 所示,齿轮 2 既绕自 身轴线 O2 转动,又随构件 H 绕几何轴线 OH 转动
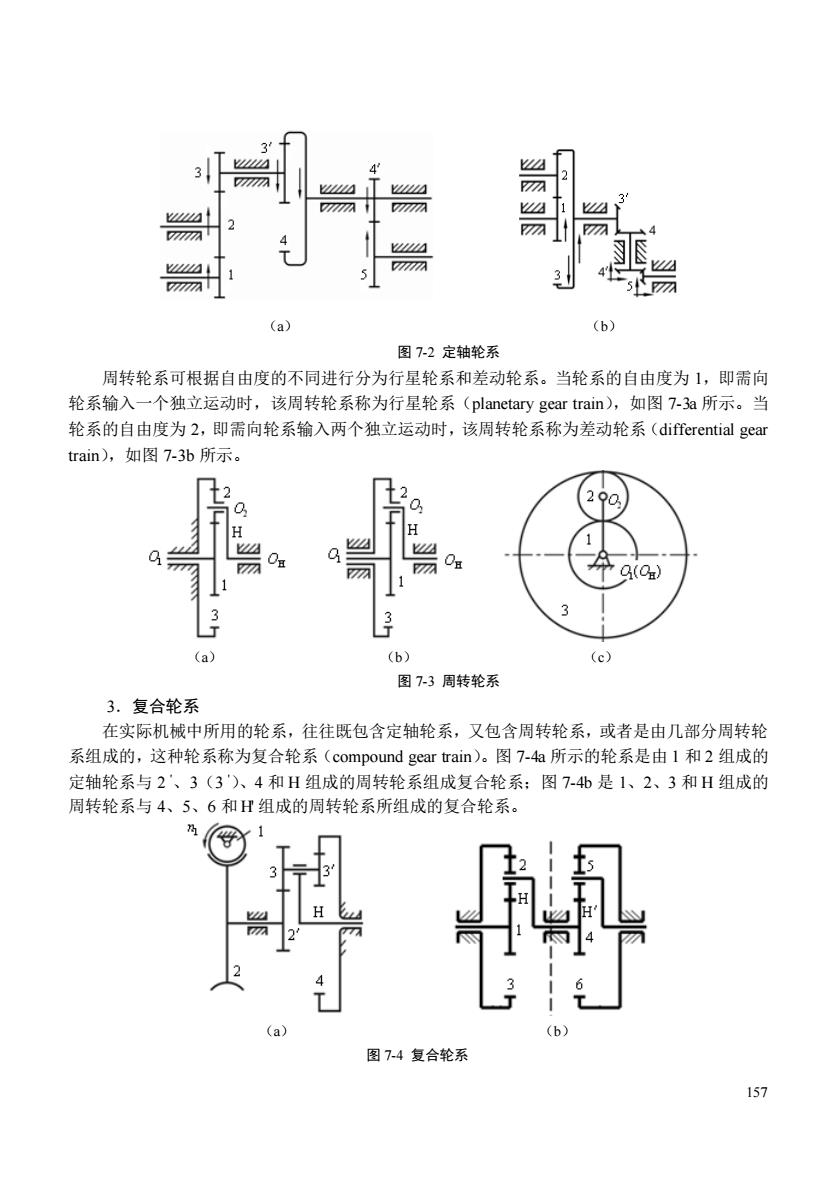
图7-2定轴轮系 周转轮系可根据自由度的不同进行分为行星轮系和差动轮系。当轮系的自由度为1,即需向 轮系输入一个独立运动时,该周转轮系称为行星轮系(planetary gear train),如图7-3a所示。当 轮系的自由度为2,即需向轮系输入两个独立运动时,该周转轮系称为差动轮系(differential gear train),如图7-3b所示。 (c) 图7-3周转轮系 3.复合轮系 在实际机械中所用的轮系,往往既包含定轴轮系,又包含周转轮系,或者是由几部分周转轮 系组成的,这种轮系称为复合轮系(compound gear train)。图7-4a所示的轮系是由1和2组成的 定轴轮系与2'、3(3')、4和H组成的周转轮系组成复合轮系:图7-4化是1、2、3和H组成的 周转轮系与4、5、6和H组成的周转轮系所组成的复合轮系。 图7-4复合轮系 157
157 (a) (b) 图 7-2 定轴轮系 周转轮系可根据自由度的不同进行分为行星轮系和差动轮系。当轮系的自由度为 1,即需向 轮系输入一个独立运动时,该周转轮系称为行星轮系(planetary gear train),如图 7-3a 所示。当 轮系的自由度为 2,即需向轮系输入两个独立运动时,该周转轮系称为差动轮系(differential gear train),如图 7-3b 所示。 (a) (b) (c) 图 7-3 周转轮系 3.复合轮系 在实际机械中所用的轮系,往往既包含定轴轮系,又包含周转轮系,或者是由几部分周转轮 系组成的,这种轮系称为复合轮系(compound gear train)。图 7-4a 所示的轮系是由 1 和 2 组成的 定轴轮系与 2 '、3(3 ')、4 和 H 组成的周转轮系组成复合轮系;图 7-4b 是 1、2、3 和 H 组成的 周转轮系与 4、5、6 和 H' 组成的周转轮系所组成的复合轮系。 (a) (b) 图 7-4 复合轮系

7.2定轴轮系传动比 定轴轮系的传动比是指,轮系中输入轴与输出轴的角速度(或转速)之比,用:表示。设轮 系的输入轴为a,输出轴为b,则轮系的传动比为i=a。/,=n,/m6,其中a和n分别为轴的 角速度与转速。定轴轮系的传动比包括传动比的大小计算和输入轴与输出轴的相对转向关系的判 定两方面。 7.2.1定轴轮系传动比大小的计算 如图7-5所示的定轴轮系,其中1为输入轴,5为输出轴,各轮齿数分别为1、2、2、 3、3、:4和:5,显然该轮系中各对齿轮副的传动比分别为 032 上述各式两边连乘后得 岛。品子吾子 对上式整理后,可以求得 (7-1 51525324 图75平面定轴轮系 上式表明,定轴轮系的传动比等于轮系中各对齿轮的传动比的乘积,也等于轮系中所有从 动轮齿数的乘积与所有主动轮齿数的乘积之比,即 158
158 7.2 定轴轮系传动比 定轴轮系的传动比是指,轮系中输入轴与输出轴的角速度(或转速)之比,用 i 表示。设轮 系的输入轴为 a,输出轴为 b,则轮系的传动比为 ab a b a b i = / = n / n ,其中 和 n 分别为轴的 角速度与转速。定轴轮系的传动比包括传动比的大小计算和输入轴与输出轴的相对转向关系的判 定两方面。 7.2.1 定轴轮系传动比大小的计算 如图 7-5 所示的定轴轮系,其中 1 为输入轴,5 为输出轴,各轮齿数分别为 1 z 、 2 z 、 2 ' z 、 3 z 、 3 ' z 、 4 z 和 5 z ,显然该轮系中各对齿轮副的传动比分别为 1 2 2 1 12 z z i = = 2' 3 3 2' 2' 3 z z i = = 3' 4 4 3' 3'4 z z i = = 4 5 5 4 45 z z i = = 上述各式两边连乘后得 4 5 3' 4 2' 3 1 2 5 4 4 3' 3 2' 2 1 12 2' 3 3'4 45 z z z z z z z z i i i i = = 对上式整理后,可以求得 1 2' 3' 4 2 3 4 5 4 5 3' 4 2' 3 1 2 12 2' 3 3'4 45 5 1 15 z z z z z z z z z z z z z z z z i = = i i i i = = (7-1) 图 7-5 平面定轴轮系 上式表明,定轴轮系的传动比等于轮系中各对齿轮的传动比的乘积,也等于轮系中所有从 动轮齿数的乘积与所有主动轮齿数的乘积之比,即
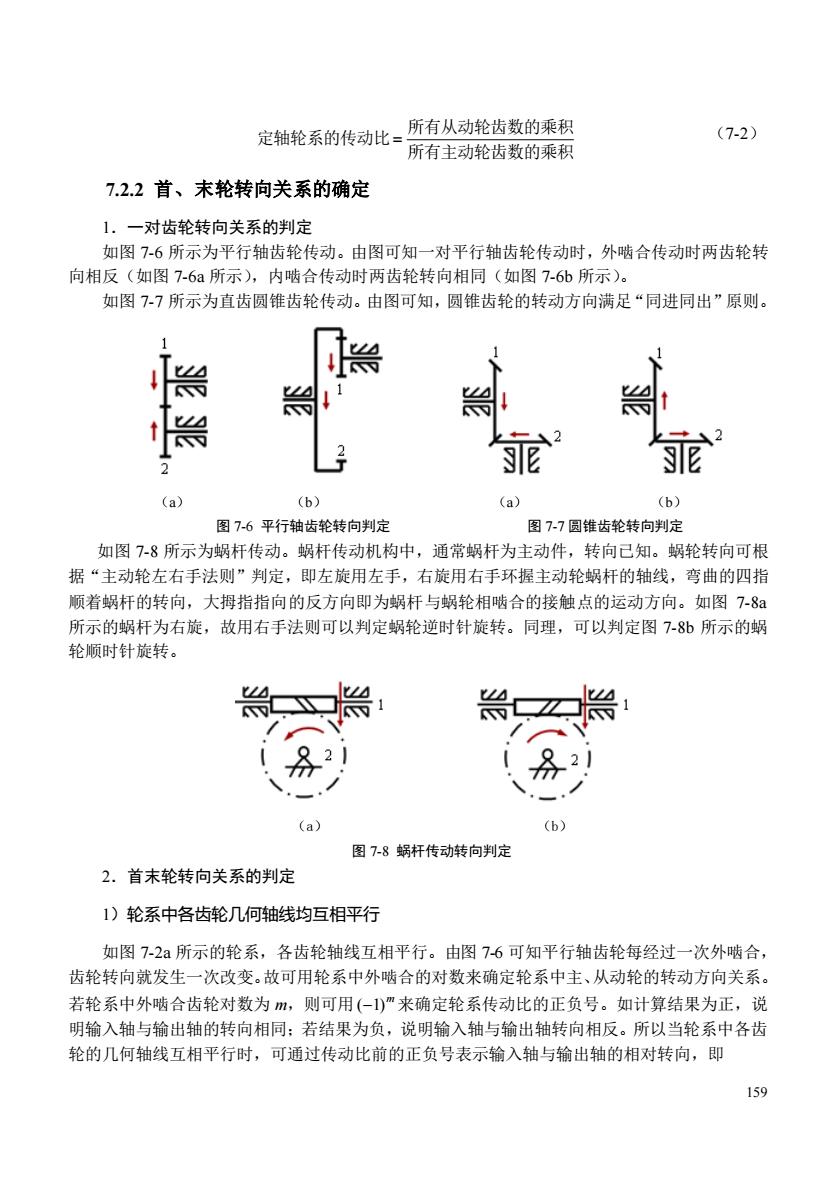
定轴轮系的传动比=所有从动轮齿数的乘积 (7-2) 所有主动轮齿数的乘积 7.2.2首、末轮转向关系的确定 1.一对齿轮转向关系的判定 如图7-6所示为平行轴齿轮传动。由图可知一对平行轴齿轮传动时,外啮合传动时两齿轮转 向相反(如图7-6a所示),内啮合传动时两齿轮转向相同(如图7-6b所示) 如图77所示为直齿圆锥齿轮传动。由图可知,圆锥齿轮的转动方向满足“同进同出”原则。 (a) (b) (a) (b) 图7:6平行轴货轮转向判圳定 图77圆锥齿轮转向判定 如图7-8所示为蜗杆传动。蜗杆传动机构中,通常蜗杆为主动件,转向己知。蜗轮转向可根 据“主动轮左右手法则”判定,即左旋用左手,右旋用右手环握主动轮蜗杆的轴线,弯曲的四指 顺着蜗杆的转向,大拇指指向的反方向即为蜗杆与蜗轮相啮合的接触点的运动方向。如图7-8a 所示的蜗杆为右旋,故用右手法则可以判定蜗轮逆时针旋转。同理,可以判定图7-8b所示的蜗 轮顺时针旋转。 821 2 分 (a) (b) 图7-8蜗杆传动转向判定 2.首未轮转向关系的判定 1)轮系中各齿轮几何轴线均互相平行 如图7-2所示的轮系,各齿轮轴线互相平行。由图7-6可知平行轴齿轮每经过一次外啮合, 齿轮转向就发生一次改变。故可用轮系中外啮合的对数来确定轮系中主、从动轮的转动方向关系。 若轮系中外啮合齿轮对数为m,则可用(-)"来确定轮系传动比的正负号。如计算结果为正,说 明输入轴与输出轴的转向相同:若结果为负,说明输入轴与输出轴转向相反。所以当轮系中各齿 轮的几何轴线互相平行时,可通过传动比前的正负号表示输入轴与输出轴的相对转向,即 159
159 所有主动轮齿数的乘积 所有从动轮齿数的乘积 定轴轮系的传动比 = (7-2) 7.2.2 首、末轮转向关系的确定 1.一对齿轮转向关系的判定 如图 7-6 所示为平行轴齿轮传动。由图可知一对平行轴齿轮传动时,外啮合传动时两齿轮转 向相反(如图 7-6a 所示),内啮合传动时两齿轮转向相同(如图 7-6b 所示)。 如图 7-7 所示为直齿圆锥齿轮传动。由图可知,圆锥齿轮的转动方向满足“同进同出”原则。 (a) (b) (a) (b) 图 7-6 平行轴齿轮转向判定 图 7-7 圆锥齿轮转向判定 如图 7-8 所示为蜗杆传动。蜗杆传动机构中,通常蜗杆为主动件,转向已知。蜗轮转向可根 据“主动轮左右手法则”判定,即左旋用左手,右旋用右手环握主动轮蜗杆的轴线,弯曲的四指 顺着蜗杆的转向,大拇指指向的反方向即为蜗杆与蜗轮相啮合的接触点的运动方向。如图 7-8a 所示的蜗杆为右旋,故用右手法则可以判定蜗轮逆时针旋转。同理,可以判定图 7-8b 所示的蜗 轮顺时针旋转。 (a) (b) 图 7-8 蜗杆传动转向判定 2.首末轮转向关系的判定 1)轮系中各齿轮几何轴线均互相平行 如图 7-2a 所示的轮系,各齿轮轴线互相平行。由图 7-6 可知平行轴齿轮每经过一次外啮合, 齿轮转向就发生一次改变。故可用轮系中外啮合的对数来确定轮系中主、从动轮的转动方向关系。 若轮系中外啮合齿轮对数为 m,则可用 m (−1) 来确定轮系传动比的正负号。如计算结果为正,说 明输入轴与输出轴的转向相同;若结果为负,说明输入轴与输出轴转向相反。所以当轮系中各齿 轮的几何轴线互相平行时,可通过传动比前的正负号表示输入轴与输出轴的相对转向,即
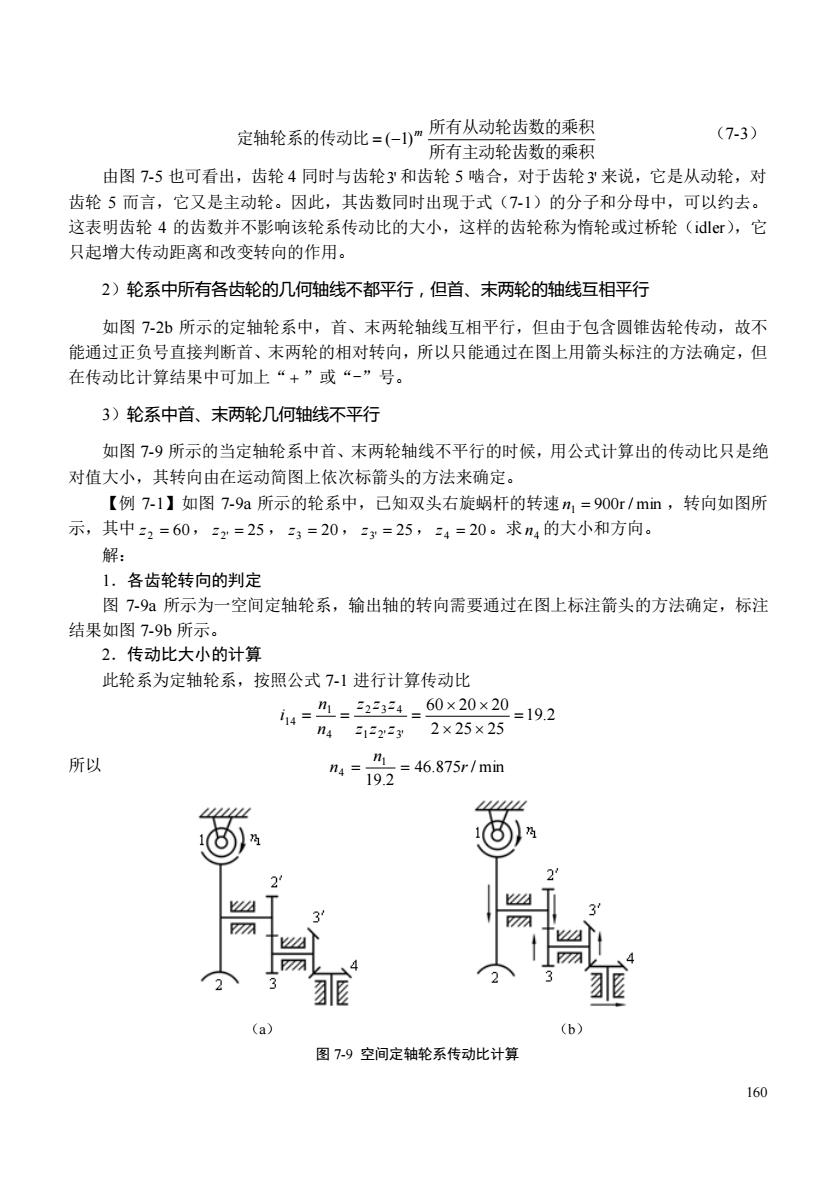
定轴轮系的传动此=~)所有从动轮齿数的乘积 (7-3) 所有主动轮齿数的乘积 由图75也可看出,齿轮4同时与齿轮3和齿轮5啮合,对于齿轮3来说,它是从动轮,对 齿轮5而言,它又是主动轮。因此,其齿数同时出现于式(7-1)的分子和分母中,可以约去。 这表明齿轮4的齿数并不影响该轮系传动比的大小,这样的齿轮称为惰轮或过桥轮(idl©r),它 只起增大传动距离和改变转向的作用。 2)轮系中所有各齿轮的几何轴线不都平行,但首、末两轮的轴线互相平行 如图7-2b所示的定轴轮系中,首、末两轮轴线互相平行,但由于包含圆锥齿轮传动,故不 能通过正负号直接判断首、末两轮的相对转向,所以只能通过在图上用箭头标注的方法确定,但 在传动比计算结果中可加上“+”或“-”号。 3)轮系中首、未两轮几何轴线不平行 如图7-9所示的当定轴轮系中首、末两轮轴线不平行的时候,用公式计算出的传动比只是绝 对值大小,其转向由在运动简图上依次标箭头的方法来确定。 【例7-1】如图7-9a所示的轮系中,已知双头右旋蜗杆的转速m1=900r/mn,转向如图所 示,其中2=60,2=25,3=20,y=25,4=20。求m,的大小和方向。 解: 1.各齿轮转向的判定 图79所示为一空间定轴轮系,输出轴的转向需要通过在图上标注箭头的方法确定,标注 结果如图7-9%6所示。 2.传动比大小的计算 此轮系为定轴轮系,按照公式7-1进行计算传动比 44-4=54-60×20×20-192 n4512x2×25×25 所以 M=02=46875r1mn 8)% (a) (b) 图7-9空间定轴轮系传动此计算 160
160 所有主动轮齿数的乘积 所有从动轮齿数的乘积 定轴轮系的传动比 m = (−1) (7-3) 由图 7-5 也可看出,齿轮 4 同时与齿轮 3' 和齿轮 5 啮合,对于齿轮 3' 来说,它是从动轮,对 齿轮 5 而言,它又是主动轮。因此,其齿数同时出现于式(7-1)的分子和分母中,可以约去。 这表明齿轮 4 的齿数并不影响该轮系传动比的大小,这样的齿轮称为惰轮或过桥轮(idler),它 只起增大传动距离和改变转向的作用。 2)轮系中所有各齿轮的几何轴线不都平行,但首、末两轮的轴线互相平行 如图 7-2b 所示的定轴轮系中,首、末两轮轴线互相平行,但由于包含圆锥齿轮传动,故不 能通过正负号直接判断首、末两轮的相对转向,所以只能通过在图上用箭头标注的方法确定,但 在传动比计算结果中可加上“ + ”或“-”号。 3)轮系中首、末两轮几何轴线不平行 如图 7-9 所示的当定轴轮系中首、末两轮轴线不平行的时候,用公式计算出的传动比只是绝 对值大小,其转向由在运动简图上依次标箭头的方法来确定。 【例 7-1】如图 7-9a 所示的轮系中,已知双头右旋蜗杆的转速 n1 = 900r / min ,转向如图所 示,其中 z 2 = 60, z2' = 25 , z3 = 20, z3' = 25, z 4 = 20 。求 4 n 的大小和方向。 解: 1.各齿轮转向的判定 图 7-9a 所示为一空间定轴轮系,输出轴的转向需要通过在图上标注箭头的方法确定,标注 结果如图 7-9b 所示。 2.传动比大小的计算 此轮系为定轴轮系,按照公式 7-1 进行计算传动比 19.2 2 25 25 60 20 20 1 2' 3' 2 3 4 4 1 14 = = = = z z z z z z n n i 所以 46.875 / min 19.2 1 4 r n n = = (a) (b) 图 7-9 空间定轴轮系传动比计算

7.3周转轮系传动比 7.3.1周转轮系的组成 如图7-3所示,齿轮2既绕自身轴线O,回转,又随构件H绕0:转动,它的运动像太阳系 中的行星运行一样,既有自转又有公转,故这种齿轮称为行星轮(planetary gear)。齿轮1和齿 轮3绕固定轴线转动,称为太阳轮(sun gear)。安装行星轮的可转动构件H称为行星架、转臂 或系杆(planet carrier)。一个系杆上的行星轮可以是一个也可以是多个。一个或多个相互啮合的 行星轮和安装这些行星轮的系杆,以及与这些行星轮相啮合的太阳轮就构成了一个周转轮系。周 转轮系的太阳轮与系杆的回转轴线必须共线,否则轮系不能运转。 由于太阳轮与系杆的回转轴均安装在机架上,便于运动和 动力的输入与输出,故周转轮系一般都以太阳轮和系杆作为运 动和动力输入或输出的构件,因此,它们称为周转轮系的基本 构件(basic link)。通常用K表示太阳轮,H表示系杆。 周转轮系可以按基本构件的不同进行分为2K-H型周转轮 系和3K型的周转轮系。如图7-3所示的周转轮系中由于有两个 太阳轮,则称为2KH型周转轮系:如图7-10所示的周转轮系 中由于有三个太阳轮,则称为3K型的周转轮系。在实际生产中, 应用最多的是2K-H型的周转轮系。 图7-103K型周转轮系 7.3.2周转轮系传动比的计算 由于周转轮系中不是所有的齿轮都做定轴转动,所以其传动比不能直接按照定轴轮系的传动 比来计算。要根据相对运动原理把它转化成定轴轮系再求其传动比。 如图7-11所示,若给整个周转轮系加上一个公共角速度“-@:”,使之绕行星架的固定轴 线回转,这时各构件之间的相对运动仍将保持不变,而行星架的角速度变为一=0,这样 周转轮系就转化成了定轴轮系。这种采用反转法原理转化所成的定轴轮系称为原周转轮系的转化 轮系(inverted gear train)。转化轮系为定轴轮系,其传动比可以按照求定轴轮系传动比的方法来 求。于是可得该转化轮系中各个构件的角速度为 0H =0-0u o=02-01 o5=03-04 @H =0 转化轮系的传动比 =-1=- o-ou 161
161 7.3 周转轮系传动比 7.3.1 周转轮系的组成 如图 7-3 所示,齿轮 2 既绕自身轴线 O2 回转,又随构件 H 绕 OH 转动,它的运动像太阳系 中的行星运行一样,既有自转又有公转,故这种齿轮称为行星轮(planetary gear)。齿轮 1 和齿 轮 3 绕固定轴线转动,称为太阳轮(sun gear)。安装行星轮的可转动构件 H 称为行星架、转臂 或系杆(planet carrier)。一个系杆上的行星轮可以是一个也可以是多个。一个或多个相互啮合的 行星轮和安装这些行星轮的系杆,以及与这些行星轮相啮合的太阳轮就构成了一个周转轮系。周 转轮系的太阳轮与系杆的回转轴线必须共线,否则轮系不能运转。 由于太阳轮与系杆的回转轴均安装在机架上,便于运动和 动力的输入与输出,故周转轮系一般都以太阳轮和系杆作为运 动和动力输入或输出的构件,因此,它们称为周转轮系的基本 构件(basic link)。通常用 K 表示太阳轮,H 表示系杆。 周转轮系可以按基本构件的不同进行分为 2K-H 型周转轮 系和 3K 型的周转轮系。如图 7-3 所示的周转轮系中由于有两个 太阳轮,则称为 2K-H 型周转轮系;如图 7-10 所示的周转轮系 中由于有三个太阳轮,则称为 3K 型的周转轮系。在实际生产中, 应用最多的是 2K-H 型的周转轮系。 7.3.2 周转轮系传动比的计算 由于周转轮系中不是所有的齿轮都做定轴转动,所以其传动比不能直接按照定轴轮系的传动 比来计算。要根据相对运动原理把它转化成定轴轮系再求其传动比。 如图 7-11 所示,若给整个周转轮系加上一个公共角速度“− H ”, 使之绕行星架的固定轴 线回转,这时各构件之间的相对运动仍将保持不变,而行星架的角速度变为 H − H = 0 ,这样 周转轮系就转化成了定轴轮系。这种采用反转法原理转化所成的定轴轮系称为原周转轮系的转化 轮系(inverted gear train)。转化轮系为定轴轮系,其传动比可以按照求定轴轮系传动比的方法来 求。于是可得该转化轮系中各个构件的角速度为 1 H H 1 = − 2 H H 2 = − 3 H H 3 = − 0 H H = 转化轮系的传动比 1 3 3 H 1 H H 3 H H 1 13 z z i = − − − = = 图 7-10 3K 型周转轮系

其中“-”表示在转化轮系中轮®与轮的转向相反。上式包含了周转轮系中三个基本构件的 角速度与各齿轮数之间的关系。当已知、,和®:中任意两个角速度矢量的大小、方向和轮 系中各齿轮的齿数时,就可以确定出第三个角速度矢量的大小和方向,从而可以进一步求出任意 两个基本构件之间的传动比。 根据上述原理,可以得出周转轮系传动比的一般关系式。设周转轮系中的两个太阳轮分别为 m和n,行星架为H,则其转化轮系的传动比为 (7.4) 转化轮系转化齿轮m至齿轮间各从动轮齿数的乘积 =±转化轮系转化齿轮m至齿轮间各主动轮齿数的乘积 =- ■ (a) (b) (c) 图7-11周转轮系的转化 特别注意: (1)公式中的“+”、“_”号与两太阳轮的真实转向无关,即“+”号,并不表示两太阳轮 的真实转向一定相同,“-”号也并不表示两太阳轮的真实转向一定相反,它仅表示在转化轮系中, 两个构件m、n的相对运动关系,可以称为是周转轮系的“结构特征”符号。 (2)H≠1m,H为转化轮系中轮m和轮n的转速之比,其大小和正负号由定轴轮系传 动比计算方法确定:而则是周转轮系中轮m和轮n的转速之比,其大小和正负号必须由计算结 果确定。 (3)公式中的0m、0.和04必须为平行矢量时才能进行代数相加减,也就是说必须是轴 线相互平行或重合的齿轮、系杆的角速度。 (4)将0。、0,和o1的已知量代入公式进行计算时,必须代入正负号。所以在计算前往 往应先假定某一方向的转速为正,则其他转速与其相同者为正,反之为负。 若所研究的轮系为具有固定轮的行星轮系,设固定轮为n,则®。=0,则可得 162
162 其中“-”表示在转化轮系中轮 H 1 与轮 H 3 的转向相反。上式包含了周转轮系中三个基本构件的 角速度与各齿轮数之间的关系。当已知 1、 3 和 H 中任意两个角速度矢量的大小、方向和轮 系中各齿轮的齿数时,就可以确定出第三个角速度矢量的大小和方向,从而可以进一步求出任意 两个基本构件之间的传动比。 根据上述原理,可以得出周转轮系传动比的一般关系式。设周转轮系中的两个太阳轮分别为 m 和 n,行星架为 H,则其转化轮系的传动比为 转化轮系转化齿轮 至齿轮 间各主动轮齿数的乘积 转化轮系转化齿轮 至齿轮 间各从动轮齿数的乘积 m n m n i = − − = = n H m H H n H H m mn (7-4) (a) (b) (c) 图 7-11 周转轮系的转化 特别注意: (1)公式中的“+”、“-”号与两太阳轮的真实转向无关,即“+”号,并不表示两太阳轮 的真实转向一定相同,“-”号也并不表示两太阳轮的真实转向一定相反,它仅表示在转化轮系中, 两个构件 m、n 的相对运动关系,可以称为是周转轮系的“结构特征”符号。 (2) mn H mn i i , H mn i 为转化轮系中轮 m 和轮 n 的转速之比,其大小和正负号由定轴轮系传 动比计算方法确定;而则是周转轮系中轮 m 和轮 n 的转速之比,其大小和正负号必须由计算结 果确定。 (3)公式中的 m 、 n 和 H 必须为平行矢量时才能进行代数相加减,也就是说必须是轴 线相互平行或重合的齿轮、系杆的角速度。 (4)将 m 、 n 和 H 的已知量代入公式进行计算时,必须代入正负号。所以在计算前往 往应先假定某一方向的转速为正,则其他转速与其相同者为正,反之为负。 若所研究的轮系为具有固定轮的行星轮系,设固定轮为 n,则 n = 0 ,则可得

温-5---9-1=1-0=1-i oH0a-0u 整理后得 ia=1-点 (7-5) 【例7-2】如图7-11a所示的2K-H轮系中,已知1=2=20,51=60。求 (1)若轮3固定,求m:(2)若m1=1,3=-1,求m和。 :(1)当轮3固定,该轮系为自由度等于1的行星轮系,对该轮系转化后,按式(74) 求得 增 0a,-0 60-3 将上述结论代入式(7-5)求得 4m=1-借=1-(-3)=4 结果为正值,表明齿轮1和系杆H转向相同。也就是说,当太阳轮1转1圈时,系杆H同向转4 圈。 (2)若轮1、3均不固定,此时该轮系为差动轮系,仍然按照转化轮系公式(74)进行计算。 并把已知条件带入 洛 60 整理后可以求得 进一步求得 结果为负值,表明齿轮1和系杆H转向相反。也就是说,当太阳轮1转1圈时,系杆H反 向转112圈。 【例7-3】如图7-12所示的双排2K-H型周转轮系,试求 (1)已知1==100,52=101,93=99时的m。 (2)己知1=2=100,52=101,3=100时的 解:(1)由图7-12可知,太阳轮3固定,所以该轮系为行星轮系,对该轮系转化后,按式 (7-4)求得 片-等-8器0器器 9999 163
163 mH H m H m H n H m H H n H H m imn =1 − =1 − i − − = − − = = 整理后得 H mH 1 mn i = − i (7-5) 【例 7-2】如图 7-11a 所示的 2K-H 轮系中,已知 z1 = z2 = 20 , z3 = 60 。求 (1)若轮 3 固定,求 1H i ;(2)若 n1 =1, n3 = −1 ,求 nH 和 1H i 。 解:(1)当轮 3 固定,该轮系为自由度等于 1 的行星轮系,对该轮系转化后,按式(7-4) 求得 3 20 60 i 1 3 3 H 1 H H 3 H H 1 13 = − = − = − − − = = z z 将上述结论代入式(7-5)求得 1 1 ( 3) 4 H i1H = − i13 = − − = 结果为正值,表明齿轮1和系杆H转向相同。也就是说,当太阳轮1转1圈时,系杆H同向转4 圈。 (2)若轮1、3均不固定,此时该轮系为差动轮系,仍然按照转化轮系公式(7-4)进行计算。 并把已知条件带入 3 20 60 1 1 i 1 3 H H 3 H 1 H H 3 H H 1 13 = − = − = − − − − = − − = = z z n n n n n n n n 整理后可以求得 2 1 nH = − 进一步求得 2 H 1 1H = = − n n i 结果为负值,表明齿轮 1 和系杆 H 转向相反。也就是说,当太阳轮 1 转 1 圈时,系杆 H 反 向转 1/ 2 圈。 【例 7-3】如图 7-12 所示的双排 2K-H 型周转轮系,试求 (1)已知 z1 = z2' =100 , z2 =101, z3 = 99 时的 1H i 。 (2)已知 z1 = z2' =100 , z2 =101, z3 =100 时的 1H i 。 解:(1)由图 7-12 可知,太阳轮 3 固定,所以该轮系为行星轮系,对该轮系转化后,按式 (7-4)求得 10000 9999 100 100 101 99 i ( 1) 1 2' 2 2 3 3 H 1 H H 3 H H 1 13 = = − = − − = = z z z z
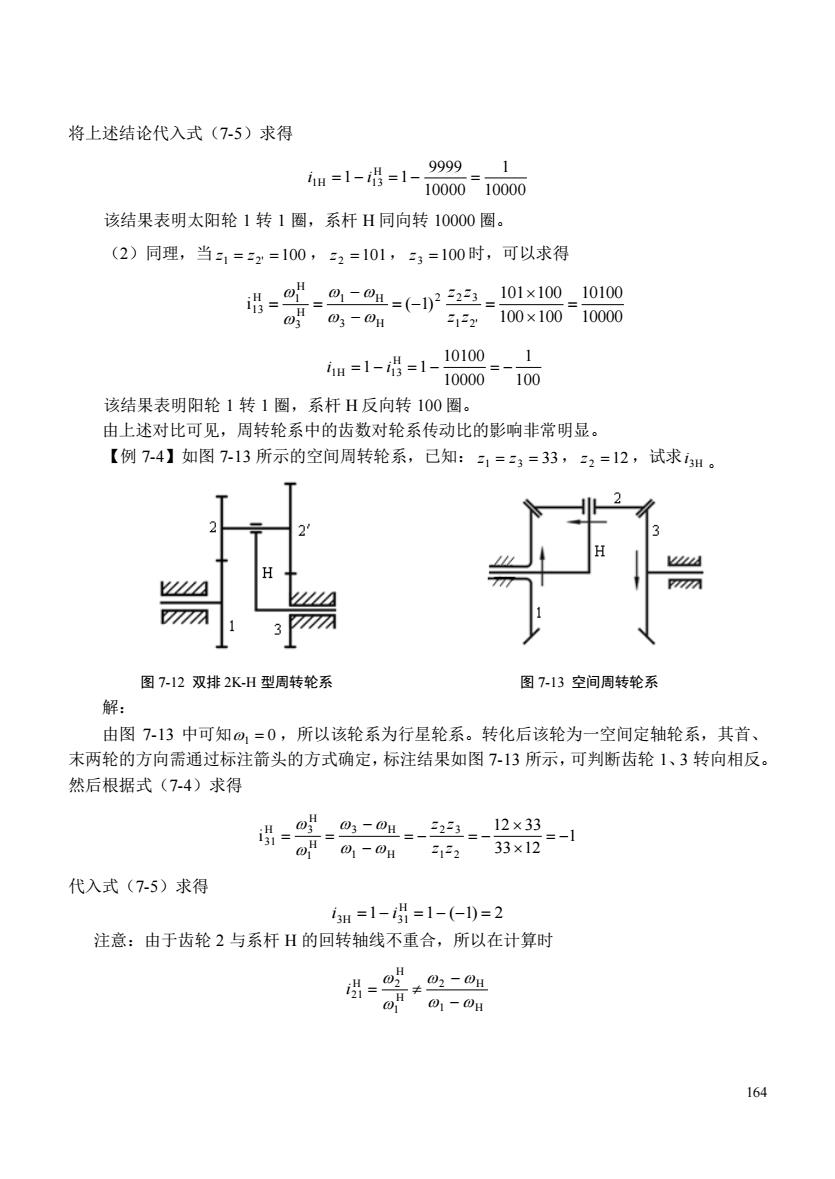
将上述结论代入式(7-5)求得 a=1-增=10d 该结果表明太阳轮1转1圈,系杆H同向转10000圈。 (2)同理,当=x=100,2=101,3=100时,可以求得 治、 ou0-Ou 少语-0调- -9二%=←129=101x10 u=1-8=1-180调d 该结果表明阳轮1转1圈,系杆H反向转100圈。 由上述对比可见,周转轮系中的齿数对轮系传动比的影响非常明显。 【例7-4】如图7-13所示的空间周转轮系,已知:1=3=33,2=12,试求组 M 图7-12双排2K-H型周转轮系 图7-13空间周转轮系 解: 由图713中可知,=0,所以该轮系为行星轮系。转化后该轮为一空间定轴轮系,其首、 末两轮的方向需通过标注箭头的方式确定,标注结果如图7-13所示,可判断齿轮1、3转向相反。 然后根据式(7-4)求得 代入式(7-5)求得 1细=1-=1-(←)=2 注意:由于齿轮2与系杆H的回转轴线不重合,所以在计算时 .02-0H - 164
164 将上述结论代入式(7-5)求得 10000 1 10000 9999 1 1 H i1H = − i13 = − = 该结果表明太阳轮 1 转 1 圈,系杆 H 同向转 10000 圈。 (2)同理,当 z1 = z2' =100 , z2 =101, z3 =100 时,可以求得 10000 10100 100 100 101 100 i ( 1) 1 2' 2 2 3 3 H 1 H H 3 H H 1 13 = = − = − − = = z z z z 100 1 10000 10100 1 1 H i1H = − i13 = − = − 该结果表明阳轮 1 转 1 圈,系杆 H 反向转 100 圈。 由上述对比可见,周转轮系中的齿数对轮系传动比的影响非常明显。 【例 7-4】如图 7-13 所示的空间周转轮系,已知: z1 = z3 = 33, z2 =12 ,试求 3H i 。 图 7-12 双排 2K-H 型周转轮系 图 7-13 空间周转轮系 解: 由图 7-13 中可知 1 = 0 ,所以该轮系为行星轮系。转化后该轮为一空间定轴轮系,其首、 末两轮的方向需通过标注箭头的方式确定,标注结果如图 7-13 所示,可判断齿轮 1、3 转向相反。 然后根据式(7-4)求得 1 33 12 12 33 i 1 2 2 3 1 H 3 H H 1 H H 3 31 = − = − = − − − = = z z z z 代入式(7-5)求得 1 1 ( 1) 2 H i3H = − i31 = − − = 注意:由于齿轮 2 与系杆 H 的回转轴线不重合,所以在计算时 1 H 2 H H 1 H H 2 21 − − i =