
第四章平面连杆机构 内容提要 本章着重讨论机械中常见的平面四杆机构。首先介绍了平面四杆机构的基本型式及其演化方 法,其次分析了平面四杆机构的运动特性和传力特性,最后介绍了平面四杆机构设计的图解法、 解析法等。 4.1概述 连杆机构(linkage mechanism)是由若干刚性构件用低副联接所组成的机构,故又称为低副 机构(lower pair mechanism)。在连杆机构中,若各运动构件均在同一平面或相互平行的平面内 运动,则称为平面连杆机构(planar linkage mechanism):若各运动构件不都在同一平面或相互平 行的平面内运动,则称为空间连杆机构(spatial linkage mechanism)。平面连杆机构的构件运动 形式多样,可实现转动、摆动、移动和平面复杂运动,也可实现已知的运动规律及轨迹,因此平 面连杆机构被广泛应用于各种机械和仪表中。如图41所示的铸造造型机砂箱翻转机构、图42 所示的车门开闭机构、图4-3所示的搅拌机构等。 平面连杆机构之所以应用如此广泛,因其具有以下显著的优点:(1)其运动副元素为面接触 压力较小,承载能力较大,且面接触便于润滑,磨损小:(2)由于两构件接触面是圆柱或平面, 加工制造方便,且易获得较高的精度:(3)两构件之间的接触是靠本身的几何封闭来维系的,不 像其它机构有时需利用弹簧或其它措施的力封闭来保持接触,对保证工作的可靠性有利。 当然平面连杆机构也存在一定的缺点:(1)一般情况下只能近似实现给定的运动规律或运动 轨迹,且设计较为复杂:(2)当给定的运动要求较多或较复杂时,需增加构件或运动副,使机构 结构复杂,积累误差增大,传动效率降低,影响其传动的精度和效率:(3)平面连杆机构中作平 面复杂运动和往复运动的构件所产生的惯性力往往难以平衡,在高速时易引起较大的振动和动载 荷,故常用于速度较低的场合。 近年来,随着连杆设计方法的发展,电子计算机的普及应用及相关设计软件的开发,连杆机 构的研究取得了长足的发展,不再局限于单自由度四杆机构的研究,也注重对多杆多自由度连杆 机构的研究,并提出了一些有关这类机构的分析及综合的方法。在设计要求上己不再局限于运动 学要求,而是同时兼顾机构的动力学特性,特别是对于高速机械,考虑构件弹性变形的运动弹性 动力学已得到很快的发展。在研究方法上,优化方法和计算机辅助设计的应用已成为研究连杆机 构的重要方法,并已相应地绵制出大量的,活用范围广、计算耗时少、使用方便的通用软件。随 着计算机的发展和现代数学工具的日益完善,以前不易解决的复杂平面连杆机构的设计问题,正 步得到解决。 分
53 第四章 平面连杆机构 内容提要 本章着重讨论机械中常见的平面四杆机构。首先介绍了平面四杆机构的基本型式及其演化方 法,其次分析了平面四杆机构的运动特性和传力特性,最后介绍了平面四杆机构设计的图解法、 解析法等。 4.1 概述 连杆机构(linkage mechanism)是由若干刚性构件用低副联接所组成的机构,故又称为低副 机构(lower pair mechanism)。在连杆机构中,若各运动构件均在同一平面或相互平行的平面内 运动,则称为平面连杆机构(planar linkage mechanism);若各运动构件不都在同一平面或相互平 行的平面内运动,则称为空间连杆机构(spatial linkage mechanism)。平面连杆机构的构件运动 形式多样,可实现转动、摆动、移动和平面复杂运动,也可实现已知的运动规律及轨迹,因此平 面连杆机构被广泛应用于各种机械和仪表中。如图 4-1 所示的铸造造型机砂箱翻转机构、图 4-2 所示的车门开闭机构、图 4-3 所示的搅拌机构等。 平面连杆机构之所以应用如此广泛,因其具有以下显著的优点:(1)其运动副元素为面接触, 压力较小,承载能力较大,且面接触便于润滑,磨损小;(2)由于两构件接触面是圆柱或平面, 加工制造方便,且易获得较高的精度;(3)两构件之间的接触是靠本身的几何封闭来维系的,不 像其它机构有时需利用弹簧或其它措施的力封闭来保持接触,对保证工作的可靠性有利。 当然平面连杆机构也存在一定的缺点:(1)一般情况下只能近似实现给定的运动规律或运动 轨迹,且设计较为复杂;(2)当给定的运动要求较多或较复杂时,需增加构件或运动副,使机构 结构复杂,积累误差增大,传动效率降低,影响其传动的精度和效率;(3)平面连杆机构中作平 面复杂运动和往复运动的构件所产生的惯性力往往难以平衡,在高速时易引起较大的振动和动载 荷,故常用于速度较低的场合。 近年来,随着连杆设计方法的发展,电子计算机的普及应用及相关设计软件的开发,连杆机 构的研究取得了长足的发展,不再局限于单自由度四杆机构的研究,也注重对多杆多自由度连杆 机构的研究,并提出了一些有关这类机构的分析及综合的方法。在设计要求上已不再局限于运动 学要求,而是同时兼顾机构的动力学特性,特别是对于高速机械,考虑构件弹性变形的运动弹性 动力学已得到很快的发展。在研究方法上,优化方法和计算机辅助设计的应用已成为研究连杆机 构的重要方法,并已相应地编制出大量的,适用范围广、计算耗时少、使用方便的通用软件。随 着计算机的发展和现代数学工具的日益完善,以前不易解决的复杂平面连杆机构的设计问题,正 逐步得到解决
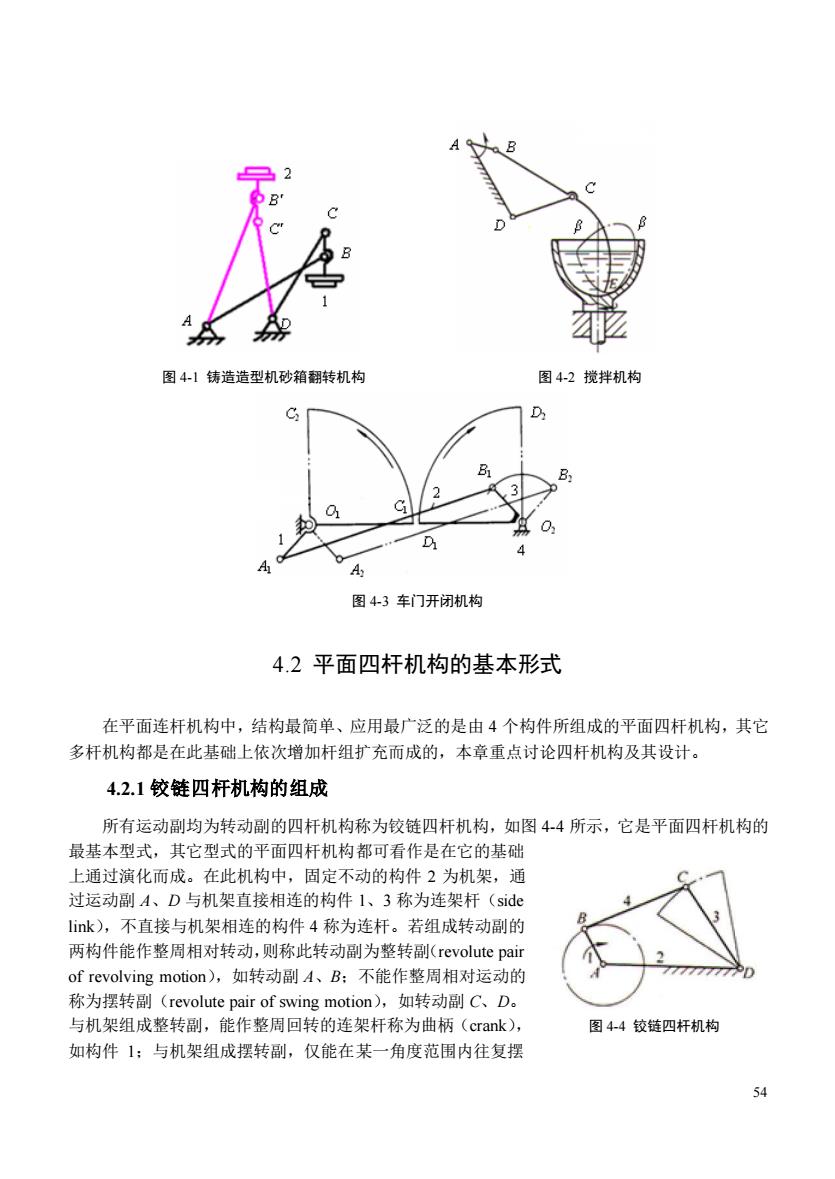
图41铸造造型机砂箱翻转机构 图42搅拌机构 D D 4 图43车门开闭机构 4.2平面四杆机构的基本形式 在平面连杆机构中,结构最简单、应用最广泛的是由4个构件所组成的平面四杆机构,其它 多杆机构都是在此基础上依次增加杆组扩充而成的,本章重点讨论四杆机构及其设计。 4.2.1铰链四杆机构的组成 所有运动副均为转动副的四杆机构称为铰链四杆机构,如图44所示,它是平面四杆机构的 最基本型式,其它型式的平面四杆机构都可看作是在它的基础 上通过演化而成。在此机构中,固定不动的构件2为机架,通 过运动副A、D与机架直接相连的构件1、3称为连架杆(side Iik),不直接与机架相连的构件4称为连杆。若组成转动副的 两构件能作整周相对转动,则称此转动副为整转副(revolute pair of revolving motion),如转动副A、B:不能作整周相对运动的 称为摆转副(revolute pair of swing motion),如转动副C、D, 与机架组成整转副,能作整周回转的连架杆称为曲柄(crak) 图44铰链四杆机构 如构件1:与机架组成摆转副,仅能在某一角度范围内往复摆
54 图 4-1 铸造造型机砂箱翻转机构 图 4-2 搅拌机构 图 4-3 车门开闭机构 4.2 平面四杆机构的基本形式 在平面连杆机构中,结构最简单、应用最广泛的是由 4 个构件所组成的平面四杆机构,其它 多杆机构都是在此基础上依次增加杆组扩充而成的,本章重点讨论四杆机构及其设计。 4.2.1 铰链四杆机构的组成 所有运动副均为转动副的四杆机构称为铰链四杆机构,如图 4-4 所示,它是平面四杆机构的 最基本型式,其它型式的平面四杆机构都可看作是在它的基础 上通过演化而成。在此机构中,固定不动的构件 2 为机架,通 过运动副 A、D 与机架直接相连的构件 1、3 称为连架杆(side link),不直接与机架相连的构件 4 称为连杆。若组成转动副的 两构件能作整周相对转动,则称此转动副为整转副(revolute pair of revolving motion),如转动副 A、B;不能作整周相对运动的 称为摆转副(revolute pair of swing motion),如转动副 C、D。 与机架组成整转副,能作整周回转的连架杆称为曲柄(crank), 如构件 1;与机架组成摆转副,仅能在某一角度范围内往复摆 图 4-4 铰链四杆机构
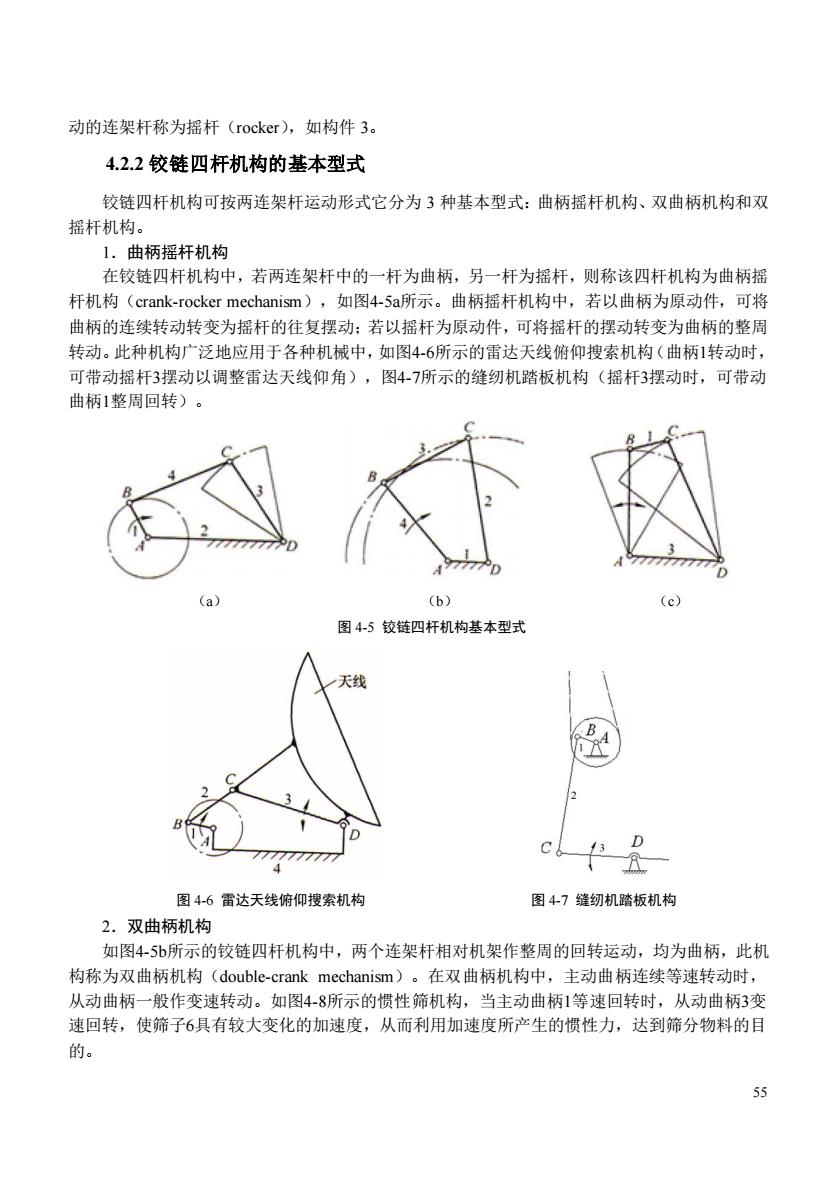
动的连架杆称为摇杆(rocker),如构件3。 4.2.2铰链四杆机构的基本型式 铰链四杆机构可按两连架杆运动形式它分为3种基本型式:曲柄摇杆机构、双曲柄机构和双 摇杆机构。 1.曲柄摇杆机构 在较链四杆机构中,若两连架杆中的一杆为曲柄,另一杆为摇杆,则称该四杆机构为曲柄摇 杆机构(crank-rocker mechanism),如图4-5a所示。曲柄摇杆机构中,若以曲柄为原动件,可将 曲柄的连续转动转变为摇杆的往复摆动:若以摇杆为原动件,可将摇杆的摆动转变为曲柄的整周 转动。此种机构广泛地应用于各种机械中,如图4-6所示的雷达天线俯仰搜索机构(曲柄1转动时, 可带动摇杆3摆动以调整雷达天线仰角),图4-7所示的缝纫机踏板机构(摇杆3摆动时,可带动 曲柄1整周回转)。 a (b) (c) 图45铰链四杆机构基本型式 天线 D 图4-6雷达天线俯仰搜索机构 图47缝纫机踏板机构 2.双曲柄机构 如图45b所示的铰链四杆机构中,两个连架杆相对机架作整周的回转运动,均为曲柄,此机 构称为双曲柄机构(double-crank mechanism)。在双曲柄机构中,主动曲柄连续等速转动时, 从动曲柄一般作变速转动。如图4-8所示的惯性筛机构,当主动曲柄1等速回转时,从动曲柄3变 速回转,使筛子6具有较大变化的加速度,从而利用加速度所产生的惯性力,达到筛分物料的目 的
55 动的连架杆称为摇杆(rocker),如构件 3。 4.2.2 铰链四杆机构的基本型式 铰链四杆机构可按两连架杆运动形式它分为 3 种基本型式:曲柄摇杆机构、双曲柄机构和双 摇杆机构。 1.曲柄摇杆机构 在铰链四杆机构中,若两连架杆中的一杆为曲柄,另一杆为摇杆,则称该四杆机构为曲柄摇 杆机构(crank-rocker mechanism),如图4-5a所示。曲柄摇杆机构中,若以曲柄为原动件,可将 曲柄的连续转动转变为摇杆的往复摆动;若以摇杆为原动件,可将摇杆的摆动转变为曲柄的整周 转动。此种机构广泛地应用于各种机械中,如图4-6所示的雷达天线俯仰搜索机构(曲柄1转动时, 可带动摇杆3摆动以调整雷达天线仰角),图4-7所示的缝纫机踏板机构(摇杆3摆动时,可带动 曲柄1整周回转)。 (a) (b) (c) 图 4-5 铰链四杆机构基本型式 图 4-6 雷达天线俯仰搜索机构 图 4-7 缝纫机踏板机构 2.双曲柄机构 如图4-5b所示的铰链四杆机构中,两个连架杆相对机架作整周的回转运动,均为曲柄,此机 构称为双曲柄机构(double-crank mechanism)。在双曲柄机构中,主动曲柄连续等速转动时, 从动曲柄一般作变速转动。如图4-8所示的惯性筛机构,当主动曲柄1等速回转时,从动曲柄3变 速回转,使筛子6具有较大变化的加速度,从而利用加速度所产生的惯性力,达到筛分物料的目 的

。E 77777 1 图48惯性筛机构 图49平行四边形机构 在双曲柄机构中,若相对两构件长度相等且平行(如图49所示),则称为平行四边形机构 (parallel-.crank mechanism)。这种机构的特点是两曲柄均以相同的角速度转动,连杆作平行移 动。但在平行四边形机构中,有一个位置不确定的问题,如图410所示,当主动曲柄运动到B 位置时,从动曲柄可有两个位置C2和C2。为解决此问题,通常采用两种方法:一是在从动曲柄 上加装一个惯性较大的轮子,利用惯性维持从动曲柄转向不变:二是通过虚约束使机构保持平行 四边形,避免机构运动位置的不确定问题,如411所示的机车车轮联动的平行四边形机构。 B 2 3 图410平行四边形机构中的位置不确定问题 图411机车车轮联动的平行四边形机构 如图412所示的双曲柄机构,两曲柄长度相同,连杆与机架不平行,主、从动曲柄转向相 反,故称为反平行四边形机构(antiparallel-crank mechanism)。图42所示的车门开闭机构即为 其应用实例,它利用反平行四边形机构运动时,两曲柄转向相反的特性,达到两扇车门同时散开 或关闭的目的。 、2 4 3 图412反平行四边形机构 3.双摇杆机构 如图4-5c所示的铰链四杆机构,两连架杆均为摇杆,则称为双摇杆机构(double-rocker mechanism)。它可把一个摇杆的摆动转变为另一个摇杆的摆动。如图4-13所示的鹤式起重机中 的四杆机构ABCD即为双摇杆机构,当主动摇杆AB摆动时,从动摇杆CD随之摆动,位于连杆 BC延长线上的重物悬挂点E将沿近似水平直线移动。在双摇杆机构中,若两摇杆的长度相等
56 图 4-8 惯性筛机构 图 4-9 平行四边形机构 在双曲柄机构中,若相对两构件长度相等且平行(如图4-9所示),则称为平行四边形机构 (parallel-crank mechanism)。这种机构的特点是两曲柄均以相同的角速度转动,连杆作平行移 动。但在平行四边形机构中,有一个位置不确定的问题,如图4-10所示,当主动曲柄运动到B2 位置时,从动曲柄可有两个位置C2和C2 '。为解决此问题,通常采用两种方法:一是在从动曲柄 上加装一个惯性较大的轮子,利用惯性维持从动曲柄转向不变;二是通过虚约束使机构保持平行 四边形,避免机构运动位置的不确定问题,如4-11所示的机车车轮联动的平行四边形机构。 图 4-10 平行四边形机构中的位置不确定问题 图 4-11 机车车轮联动的平行四边形机构 如图 4-12 所示的双曲柄机构,两曲柄长度相同,连杆与机架不平行,主、从动曲柄转向相 反,故称为反平行四边形机构(antiparallel-crank mechanism)。图 4-2 所示的车门开闭机构即为 其应用实例,它利用反平行四边形机构运动时,两曲柄转向相反的特性,达到两扇车门同时敞开 或关闭的目的。 图 4-12 反平行四边形机构 3.双摇杆机构 如图 4-5c 所示的铰链四杆机构,两连架杆均为摇杆,则称为双摇杆机构(double-rocker mechanism)。它可把一个摇杆的摆动转变为另一个摇杆的摆动。如图 4-13 所示的鹤式起重机中 的四杆机构 ABCD 即为双摇杆机构,当主动摇杆 AB 摆动时,从动摇杆 CD 随之摆动,位于连杆 BC 延长线上的重物悬挂点 E 将沿近似水平直线移动。在双摇杆机构中,若两摇杆的长度相等
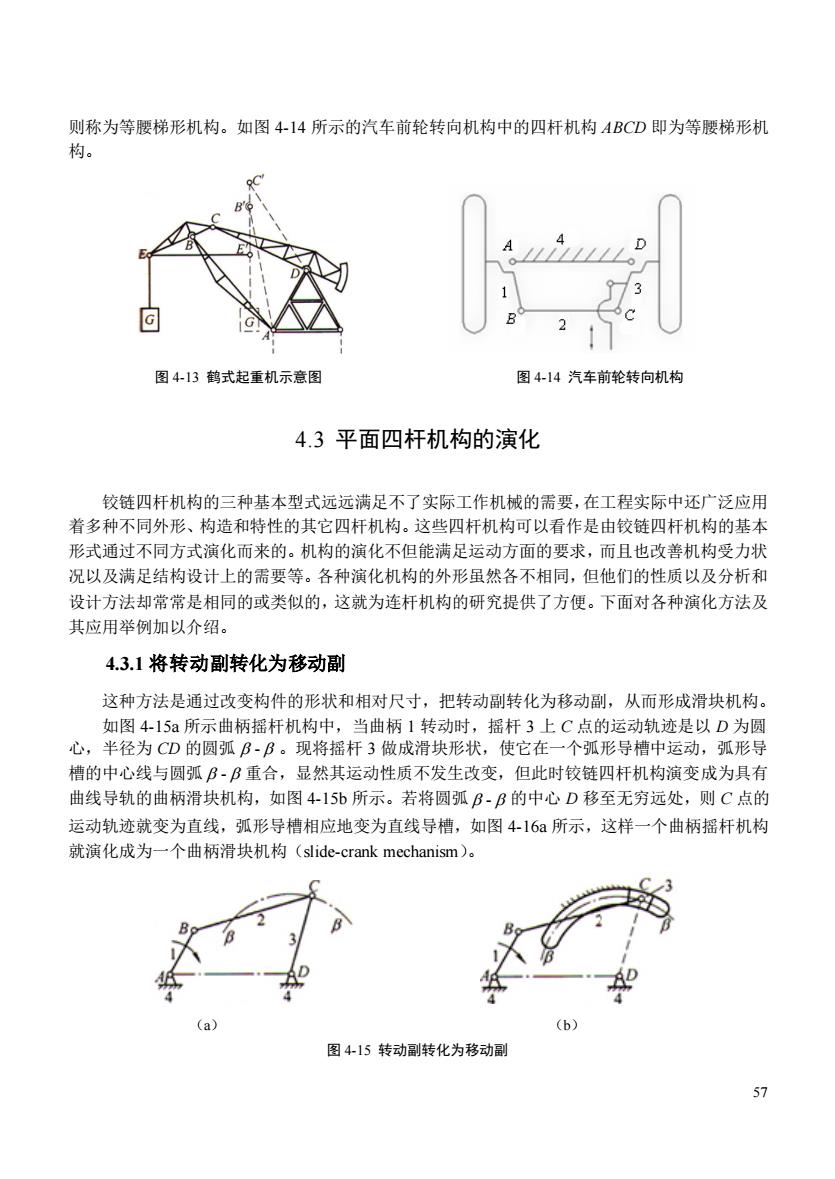
则称为等腰梯形机构。如图414所示的汽车前轮转向机构中的四杆机构ABCD即为等腰梯形机 构。 图4-13鹤式起重机示意图 图4-14汽车前轮转向机构 4.3平面四杆机构的演化 铰链四杆机构的三种基本型式远远满足不了实际工作机械的需要,在工程实际中还广泛应用 着多种不同外形、构造和特性的其它四杆机构。这些四杆机构可以看作是由铰链四杆机构的基本 形式通过不同方式演化而来的。机构的演化不但能满足运动方面的要求,而且也改善机构受力状 况以及满足结构设计上的需要等。各种演化机构的外形虽然各不相同,但他们的性质以及分析和 设计方法却常常是相同的或类似的,这就为连杆机构的研究提供了方便。下面对各种演化方法及 其应用举例加以介绍。 4.3.1将转动副转化为移动副 这种方法是通过改变构件的形状和相对尺寸,把转动副转化为移动副,从而形成滑块机构。 如图4-15a所示曲柄摇杆机构中,当曲柄1转动时,摇杆3上C点的运动轨迹是以D为圆 心,半径为CD的圆弧B-B。现将摇杆3做成滑块形状,使它在一个弧形导槽中运动,弧形导 槽的中心线与圆弧B-B重合,显然其运动性质不发生改变,但此时铰链四杆机构演变成为具有 曲线导轨的曲柄滑块机构,如图415b所示。若将圆弧B-B的中心D移至无穷远处,则C点的 运动轨迹就变为直线,弧形导槽相应地变为直线导槽,如图4-16a所示,这样一个曲柄摇杆机构 就演化成为一个曲柄滑块机构(slide--crank mechanism)。 a (b) 图415转动副转化为移动副
57 则称为等腰梯形机构。如图 4-14 所示的汽车前轮转向机构中的四杆机构 ABCD 即为等腰梯形机 构。 图 4-13 鹤式起重机示意图 图 4-14 汽车前轮转向机构 4.3 平面四杆机构的演化 铰链四杆机构的三种基本型式远远满足不了实际工作机械的需要,在工程实际中还广泛应用 着多种不同外形、构造和特性的其它四杆机构。这些四杆机构可以看作是由铰链四杆机构的基本 形式通过不同方式演化而来的。机构的演化不但能满足运动方面的要求,而且也改善机构受力状 况以及满足结构设计上的需要等。各种演化机构的外形虽然各不相同,但他们的性质以及分析和 设计方法却常常是相同的或类似的,这就为连杆机构的研究提供了方便。下面对各种演化方法及 其应用举例加以介绍。 4.3.1 将转动副转化为移动副 这种方法是通过改变构件的形状和相对尺寸,把转动副转化为移动副,从而形成滑块机构。 如图 4-15a 所示曲柄摇杆机构中,当曲柄 1 转动时,摇杆 3 上 C 点的运动轨迹是以 D 为圆 心,半径为 CD 的圆弧 - 。现将摇杆 3 做成滑块形状,使它在一个弧形导槽中运动,弧形导 槽的中心线与圆弧 - 重合,显然其运动性质不发生改变,但此时铰链四杆机构演变成为具有 曲线导轨的曲柄滑块机构,如图 4-15b 所示。若将圆弧 - 的中心 D 移至无穷远处,则 C 点的 运动轨迹就变为直线,弧形导槽相应地变为直线导槽,如图 4-16a 所示,这样一个曲柄摇杆机构 就演化成为一个曲柄滑块机构(slide-crank mechanism)。 (a) (b) 图 4-15 转动副转化为移动副

曲柄回转中心到导槽中心线之间的距离e称为偏距。当e≠0时,称为偏置曲柄滑块机构 (offset slide-.crank mechanism),如图4-l6a所示:当e=0时,称为对心曲柄滑块机构(centric slide-crank mechanism),如图4-l6b所示。冲床、内燃机、空压机等机器中广泛应用曲柄滑块机 构。 (b) 图4-16曲柄滑块机构 4.3.2取不同构件为机架 这种方法是通过取不同的构件为机架,得到不同的四杆机构。 1.变化铰链四杆机构的机架 以低副相连接的两构件之间的相对运动关系,不因选取其中哪一个构件为机架而改变,这 性质称低副运动的可逆性。 如图417a所示的曲柄摇杆机构,运动副A、B为整转副,运动副C、D为摆转副。根据低 副运动的可逆性,若选构件1为机架,则得双曲柄机构,如图417b所示:若选构件2为机架, 则得另一个曲柄摇杆机构,如图417c所示:若选构件3为机架,则得双摇杆机构,如图417 所示。 c 2 2 2 B 3 2 1 3 3 D A 4 D A 4 D (a) (b) (e) (d) 图417曲柄摇杆机构的演化 2.变化单移动副机构的机架 如图4-18a所示的对心曲柄滑块机构,若选机构中不同构件为机架时,便可以得到具有一个 移动副的不同的四杆机构。 如图418b所示,当取构件1为机架时,构件2、4就成为连架杆,它们分别以B、A为回转 中心作整周转动,而构件3则以构件4为导轨沿其相对移动。由于构件4是滑块3的导轨,故又 称构件4为导杆(guide bar),若导杆作整周转动,则称该机构为转动导杆机构(rotating guide-bar mechanism):若导杆做非整周转动,则称该机构为摆动导杆(swing guide-bar mechanism)。图 419阳所示的小型侧床中的ABC部分即为转动导杆机构:图41%所示牛头刨床的导杆机构AB( 即为摆动导杆机构
58 曲柄回转中心到导槽中心线之间的距离 e 称为偏距。当 e 0 时,称为偏置曲柄滑块机构 (offset slide-crank mechanism),如图 4-16a 所示;当 e = 0 时,称为对心曲柄滑块机构(centric slide-crank mechanism),如图 4-16b 所示。冲床、内燃机、空压机等机器中广泛应用曲柄滑块机 构。 (a) (b) 图 4-16 曲柄滑块机构 4.3.2 取不同构件为机架 这种方法是通过取不同的构件为机架,得到不同的四杆机构。 1.变化铰链四杆机构的机架 以低副相连接的两构件之间的相对运动关系,不因选取其中哪一个构件为机架而改变,这一 性质称低副运动的可逆性。 如图 4-17a 所示的曲柄摇杆机构,运动副 A、B 为整转副,运动副 C、D 为摆转副。根据低 副运动的可逆性,若选构件 1 为机架,则得双曲柄机构,如图 4-17b 所示;若选构件 2 为机架, 则得另一个曲柄摇杆机构,如图 4-17c 所示;若选构件 3 为机架,则得双摇杆机构,如图 4-17d 所示。 (a) (b) (c) (d) 图 4-17 曲柄摇杆机构的演化 2.变化单移动副机构的机架 如图 4-18a 所示的对心曲柄滑块机构,若选机构中不同构件为机架时,便可以得到具有一个 移动副的不同的四杆机构。 如图 4-18b 所示,当取构件 1 为机架时,构件 2、4 就成为连架杆,它们分别以 B、A 为回转 中心作整周转动,而构件 3 则以构件 4 为导轨沿其相对移动。由于构件 4 是滑块 3 的导轨,故又 称构件 4 为导杆(guide bar),若导杆作整周转动,则称该机构为转动导杆机构(rotating guide-bar mechanism);若导杆做非整周转动,则称该机构为摆动导杆(swing guide-bar mechanism)。图 4-19a 所示的小型刨床中的 ABC 部分即为转动导杆机构;图 4-19b 所示牛头刨床的导杆机构 ABC 即为摆动导杆机构
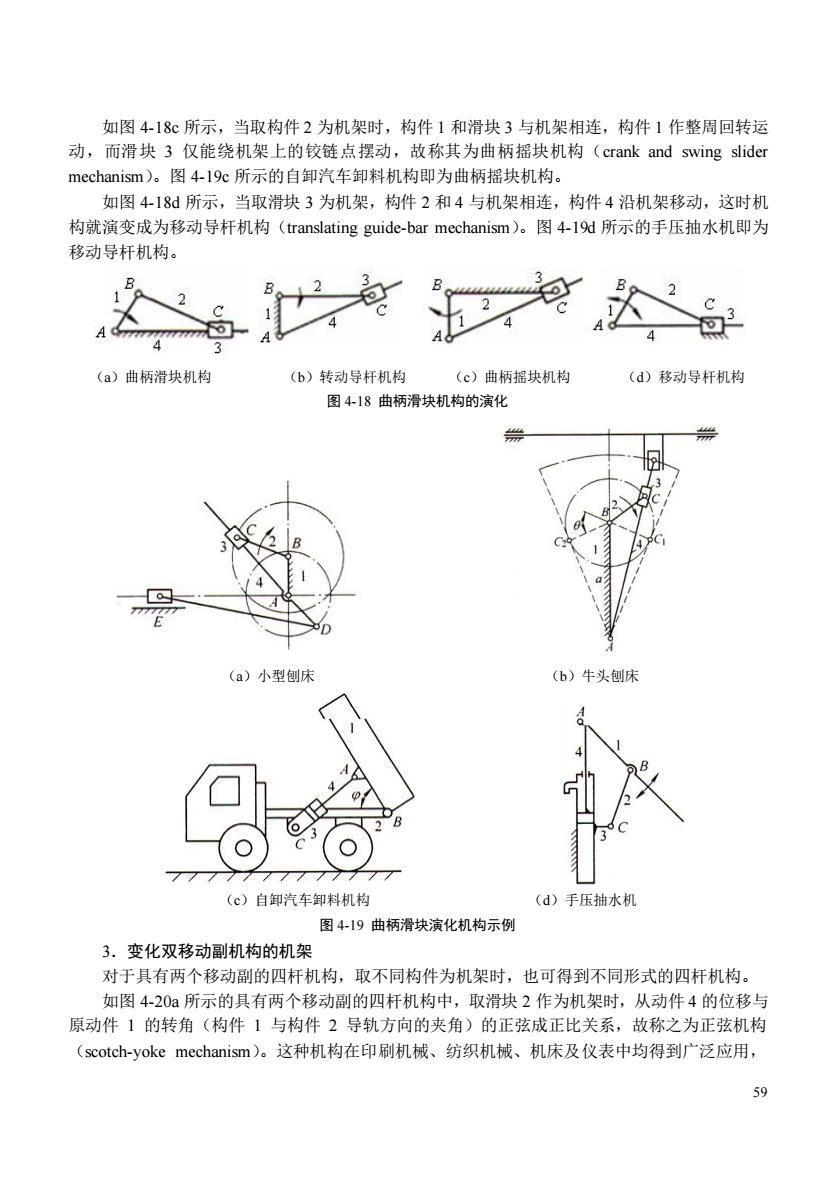
如图4-18c所示,当取构件2为机架时,构件1和滑块3与机架相连,构件1作整周回转运 动,而滑块3仅能绕机架上的铰链点摆动,故称其为曲柄摇块机构(crank and swing slider mechanism)。图419c所示的自卸汽车卸料机构即为曲柄摇块机构。 如图4-18所示,当取滑块3为机架,构件2和4与机架相连,构件4沿机架移动,这时机 构就演变成为移动导杆机构(translating guide-.bar mechanism)。图41u所示的手压抽水机即为 移动导杆机构。 a)曲柄滑块机构 (6)转动导杆机构 (c)曲柄摇块机构 (d)移动导杆机 图418曲柄滑块机构的演化 (a)小型刨床 (b)牛头创床 6出 (©)自卸汽车卸料机构 (d)手压抽水机 图419曲柄滑块演化机构示例 3.变化双移动副机构的机架 对干具有两个移动剧的四杆机构,取不同构件为机架村,也口得到不同形式的四杆机构 如图4-20a所示的具有两个移动副的四杆机构中,取滑块2作为机架时,从动件4的位移与 原动件1的转角(构件1与构件2导轨方向的夹角)的正弦成正比关系,故称之为正弦机构 (scotch--yoke mechanism)。这种机构在印刷机械、纺织机械、机床及仪表中均得到广泛应用, 9
59 如图 4-18c 所示,当取构件 2 为机架时,构件 1 和滑块 3 与机架相连,构件 1 作整周回转运 动,而滑块 3 仅能绕机架上的铰链点摆动,故称其为曲柄摇块机构(crank and swing slider mechanism)。图 4-19c 所示的自卸汽车卸料机构即为曲柄摇块机构。 如图 4-18d 所示,当取滑块 3 为机架,构件 2 和 4 与机架相连,构件 4 沿机架移动,这时机 构就演变成为移动导杆机构(translating guide-bar mechanism)。图 4-19d 所示的手压抽水机即为 移动导杆机构。 (a)曲柄滑块机构 (b)转动导杆机构 (c)曲柄摇块机构 (d)移动导杆机构 图 4-18 曲柄滑块机构的演化 (a)小型刨床 (b)牛头刨床 (c)自卸汽车卸料机构 (d)手压抽水机 图 4-19 曲柄滑块演化机构示例 3.变化双移动副机构的机架 对于具有两个移动副的四杆机构,取不同构件为机架时,也可得到不同形式的四杆机构。 如图 4-20a 所示的具有两个移动副的四杆机构中,取滑块 2 作为机架时,从动件 4 的位移与 原动件 1 的转角(构件 1 与构件 2 导轨方向的夹角)的正弦成正比关系,故称之为正弦机构 (scotch-yoke mechanism)。这种机构在印刷机械、纺织机械、机床及仪表中均得到广泛应用
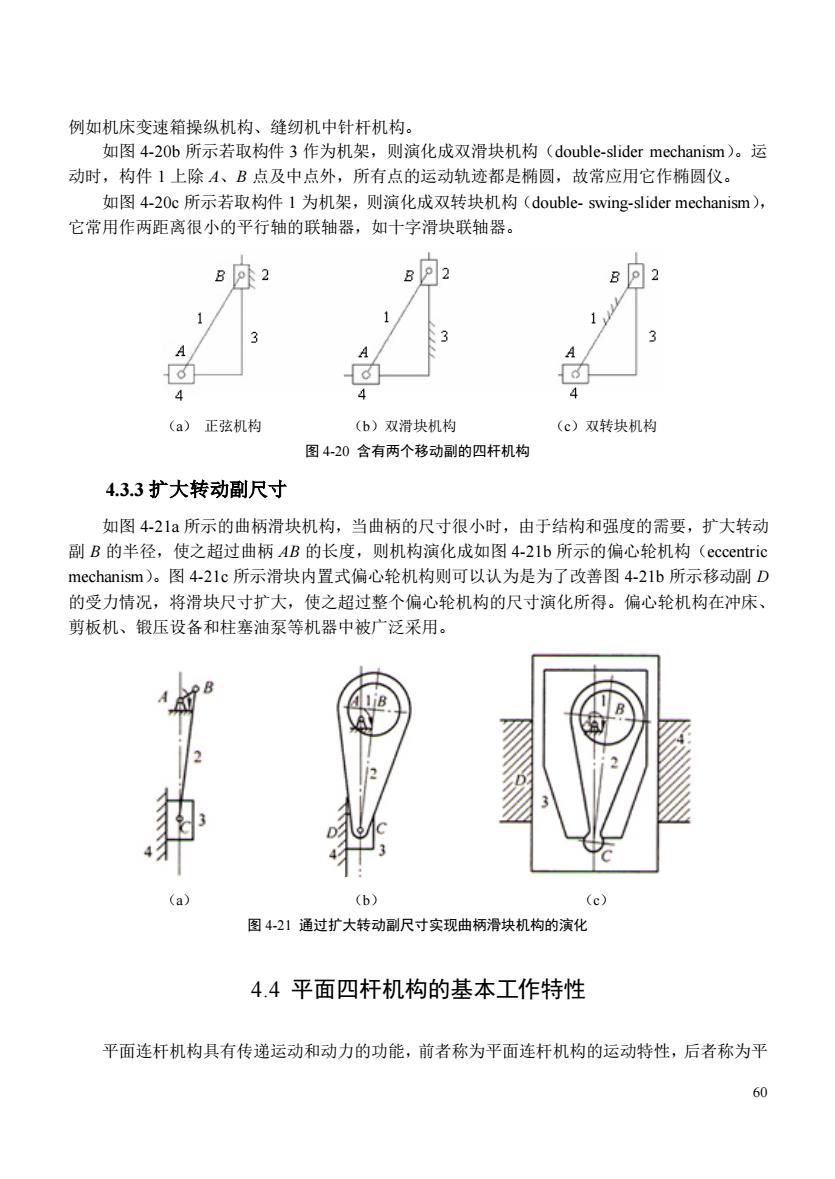
例如机床变速箱操纵机构、缝纫机中针杆机构。 如图4-2Ob所示若取构件3作为机架,则演化成双滑块机构(double--slider mechanism)。运 动时,构件1上除A、B点及中点外,所有点的运动轨迹都是椭圆,故常应用它作椭圆仪。 如图420c所示若取构件1为机架,则演化成双转块机构(double-swing-.slider mechanism) 它常用作两距离很小的平行轴的联轴器,如十字滑块联轴器。 B外2 B可2 1 4 4 (a)正弦机构 (b)双滑块机构 (c)双转块机构 图420含有两个移动副的四杆机构 4.3.3扩大转动副尺寸 如图4-21a所示的曲柄滑块机构,当曲柄的尺寸很小时,由于结构和强度的需要,扩大转动 副B的半径,使之超过曲柄AB的长度,则机构演化成如图4-2lb所示的偏心轮机构(eccentric mechanism)。图421c所示滑块内置式偏心轮机构则可以认为是为了改善图4-21b所示移动副D 的受力情况,将滑块尺寸扩大,使之超过整个偏心轮机构的尺寸演化所得。偏心轮机构在冲床、 剪板机、锻压设备和柱塞油泵等机器中被广泛采用。 (b) (c) 图4-21通过扩大转动副尺寸实现曲柄滑块机构的演化 4.4平面四杆机构的基本工作特性 平面连杆机构具有传递运动和动力的功能,前者称为平面连杆机构的运动特性,后者称为平
60 例如机床变速箱操纵机构、缝纫机中针杆机构。 如图 4-20b 所示若取构件 3 作为机架,则演化成双滑块机构(double-slider mechanism)。运 动时,构件 1 上除 A、B 点及中点外,所有点的运动轨迹都是椭圆,故常应用它作椭圆仪。 如图 4-20c 所示若取构件 1 为机架,则演化成双转块机构(double- swing-slider mechanism), 它常用作两距离很小的平行轴的联轴器,如十字滑块联轴器。 (a) 正弦机构 (b)双滑块机构 (c)双转块机构 图 4-20 含有两个移动副的四杆机构 4.3.3 扩大转动副尺寸 如图 4-21a 所示的曲柄滑块机构,当曲柄的尺寸很小时,由于结构和强度的需要,扩大转动 副 B 的半径,使之超过曲柄 AB 的长度,则机构演化成如图 4-21b 所示的偏心轮机构(eccentric mechanism)。图 4-21c 所示滑块内置式偏心轮机构则可以认为是为了改善图 4-21b 所示移动副 D 的受力情况,将滑块尺寸扩大,使之超过整个偏心轮机构的尺寸演化所得。偏心轮机构在冲床、 剪板机、锻压设备和柱塞油泵等机器中被广泛采用。 (a) (b) (c) 图 4-21 通过扩大转动副尺寸实现曲柄滑块机构的演化 4.4 平面四杆机构的基本工作特性 平面连杆机构具有传递运动和动力的功能,前者称为平面连杆机构的运动特性,后者称为平

面连杆机构的传力特性。了解这些特性,对于正确选择平面连杆机构的类型,进行机构设计具有 重要指导意义。 由于铰链四杆机构是平面四杆机构的基本形式,其他的四杆机构可认为是由它演化而来。本 节以铰链四杆机构为例,介绍其运动特性和传力特性,其结论可很方便地应用到其他形式的四杆 机构上。 4.4.1平面四杆机构的运动特性 1.铰链四杆机构中有曲柄的条件 平面四杆机构有曲柄的前提是其运动副中必有整转副存在,故先确定转动副为整转副的条 冬 如图422所示的铰链四杆机构,设各杆的长度分别为、b、c、d。要使转动副A成为整转 副,AB杆应能处于以A为圆心的圆中任何位置。由于AB杆与AD杆两次共线时可分别得到 △BCD和△B"C"D,由三角形边长关系可得 a+d≤b+c (4-1) bs(d-a)+c即a+b≤c+d (4-2) c≤(d-a)+b即a+c≤b+d (4-3) 图422转动副为整转的条件 上述各式中的等号表示当B处于B点和B”点时,A、B、C、D四点共线,这时刚好也能形成 整转副。 将式(4-1)、(4-2)和(43)分别两两相加,则得 asb,asc,asd (4.4) 如果设杆长满足d<a,则把式(4-2)和式(4-3)中的(d-a)改为(a一d),再与式(4-1) 两两相加,可得 a+d≤b+C,d+b≤c+a,d+c≤b+a (4-5) dsa,dsb,dsc (4-6) 综合分析式(41)~式(4-6),可得出铰链四杆机构中连接两构件的运动副成为整转副的 条件是 (1)被该运动副连接的两构件中必有一个构件是四杆中长度最短的构件: (2)最短构件与最长构件长度之和小于或等于其余两构件长度之和。 在有整转副存在的铰链四杆机构中,最短杆两端的转动副均为整转副。此时,若最短杆为机 61
61 面连杆机构的传力特性。了解这些特性,对于正确选择平面连杆机构的类型,进行机构设计具有 重要指导意义。 由于铰链四杆机构是平面四杆机构的基本形式,其他的四杆机构可认为是由它演化而来。本 节以铰链四杆机构为例,介绍其运动特性和传力特性,其结论可很方便地应用到其他形式的四杆 机构上。 4.4.1 平面四杆机构的运动特性 1.铰链四杆机构中有曲柄的条件 平面四杆机构有曲柄的前提是其运动副中必有整转副存在,故先确定转动副为整转副的条 件。 如图 4-22 所示的铰链四杆机构,设各杆的长度分别为 a、b、c、d。要使转动副 A 成为整转 副,AB 杆应能处于以 A 为圆心的圆中任何位置。由于 AB 杆与 AD 杆两次共线时可分别得到 △B'C'D 和 △B"C"D ,由三角形边长关系可得 a + d b + c (4-1) b (d − a) + c 即 a + b c + d (4-2) c (d − a) + b 即 a + c b + d (4-3) 图 4-22 转动副为整转副的条件 上述各式中的等号表示当B处于 B' 点和 B" 点时,A、B、C、D四点共线,这时刚好也能形成 整转副。 将式(4-1)、(4-2)和(4-3)分别两两相加,则得 a ≤ b, a ≤ c, a ≤ d (4-4) 如果设杆长满足 d a ,则把式(4-2)和式(4-3)中的(d-a)改为(a-d),再与式(4-1) 两两相加,可得 a + d ≤ b + c,d + b ≤ c + a,d + c ≤ b + a (4-5) 即 d ≤ a, d ≤ b, d ≤ c (4-6) 综合分析式(4-1)~式(4-6),可得出铰链四杆机构中连接两构件的运动副成为整转副的 条件是: (1)被该运动副连接的两构件中必有一个构件是四杆中长度最短的构件; (2)最短构件与最长构件长度之和小于或等于其余两构件长度之和。 在有整转副存在的铰链四杆机构中,最短杆两端的转动副均为整转副。此时,若最短杆为机

架,则得双曲柄机构:若最短杆为连架杆,则得曲柄摇杆机构:若最短杆为连杆,则得双摇杆机 如果四杆机构不满足杆长之和条件,则此机构中不存在整转副,这时不论选取哪个构件为机 架,所得机构均为双摇杆机构。 由此得出铰链四杆机构有曲柄的条件: (1)最短杆和最长杆长度之和小于或等于其他两杆长度之和 (2)最短轩是连架轩或机架。 2.急回运动特性 如图4-23所示的曲柄摇杆机构中,曲柄AB为原动件,摇杆CD为从动件。在原动件AB转 动一周的过程中,有两次与连杆共线,这时摇杆CD分别处于左右两极限位置CD和C,D,机构 所处的这两个位置称为极位(limit position)。机构在两个极位时,原动件AB所在两个位置之间 所夹锐角g称为极位夹角(angle between two limit positions)。 在图423中,主动曲柄AB位于AB位置(即与连杆成一直线)时,从动摇杆CD位于左极限 位置C,D。当曲柄AB以等角速度顺时针转过角α,到达位置AB,时,与连杆再次共线,而摇 杆CD则到达其右极限位置C2D,当曲柄AB继续转过角a2而回到AB位置时,摇杆CD则由极 限位置CD摆回到左极限位置C,D,从动件的往复摆角均为Q。由图可以看出,曲柄相应的两 个转角a1和a2分别为 41=180°+0,a2=180°-0 由于a>a2,因此曲柄以等角速度@转过这两个角度时,对应的时间4>2,且 4,/a2=4/12。摇杆的平均角速度为 )t=0/1,,0)、=0/1, 显然,m<o,即在曲柄等速回转情况下,从动摇杆往复摆动的平均角速度不同,一快 一慢,通常把这种运动特性,称为急回运动特性(quick-return motion)。一般为了提高机械的工 作效率,其工作行程慢速运动,提高工作质量,而空回行程快速运动,缩短辅助时间。 图423曲柄摇杆机构急回运动特性分析 为了衡量摇杆急回作用的程度,通常把从动件往复摆动平均速度的比值(大于1)称为行程 速比系数(coefficient of travel speed variation),并用K来表示,即 K=从动件快速行程平均速度。02.94.4.180°+日 从动件慢速行程平均速度omp4a42180°-0 (47)
62 架,则得双曲柄机构;若最短杆为连架杆,则得曲柄摇杆机构;若最短杆为连杆,则得双摇杆机 构。 如果四杆机构不满足杆长之和条件,则此机构中不存在整转副,这时不论选取哪个构件为机 架,所得机构均为双摇杆机构。 由此得出铰链四杆机构有曲柄的条件: (1)最短杆和最长杆长度之和小于或等于其他两杆长度之和; (2)最短杆是连架杆或机架。 2.急回运动特性 如图 4-23 所示的曲柄摇杆机构中,曲柄 AB 为原动件,摇杆 CD 为从动件。在原动件 AB 转 动一周的过程中,有两次与连杆共线,这时摇杆 CD 分别处于左右两极限位置 C1D 和 C2D ,机构 所处的这两个位置称为极位(limit position)。机构在两个极位时,原动件 AB 所在两个位置之间 所夹锐角 称为极位夹角(angle between two limit positions)。 在图4-23中,主动曲柄 AB 位于 AB1 位置(即与连杆成一直线)时,从动摇杆CD位于左极限 位置 C1D 。当曲柄 AB 以等角速度 1 顺时针转过角 1 到达位置 AB2 时,与连杆再次共线,而摇 杆 CD 则到达其右极限位置 C2D ,当曲柄 AB 继续转过角 2 而回到 AB1 位置时,摇杆 CD 则由极 限位置 C2D 摆回到左极限位置 C1D ,从动件的往复摆角均为 。由图可以看出,曲柄相应的两 个转角 1 和 2 分别为 = + 1 180 , = − 2 180 由于 1 2 ,因此曲柄以等角速度 1 转过这两个角度时,对应的时间 1 2 t t ,且 1 2 1 2 / = t /t 。摇杆的平均角速度为 m1 1 = /t , m2 2 = / t 显然, m1 m2 ,即在曲柄等速回转情况下,从动摇杆往复摆动的平均角速度不同,一快 一慢,通常把这种运动特性,称为急回运动特性(quick-return motion)。一般为了提高机械的工 作效率,其工作行程慢速运动,提高工作质量,而空回行程快速运动,缩短辅助时间。 图 4-23 曲柄摇杆机构急回运动特性分析 为了衡量摇杆急回作用的程度,通常把从动件往复摆动平均速度的比值(大于1)称为行程 速比系数(coefficient of travel speed variation),并用 K 来表示,即 − + = = = = = 180 180 2 1 1 2 m1 m2 t t K 从动件慢速行程平均速度 从动件快速行程平均速度 (4-7)