
管理运筹学 第四章单纯形法
管理运筹学 第四章 单纯形法
本章内容 1 单纯形法的基本思路和原理 2 单纯形法的表格形式 求目标函数值最小的线性规划问题的单 3 纯形表解法 几种特殊情况
单纯形法的基本思路和原理 单纯形法的表格形式 求目标函数值最小的线性规划问题的单 纯形表解法 几种特殊情况 本章内容 1 2 3 4
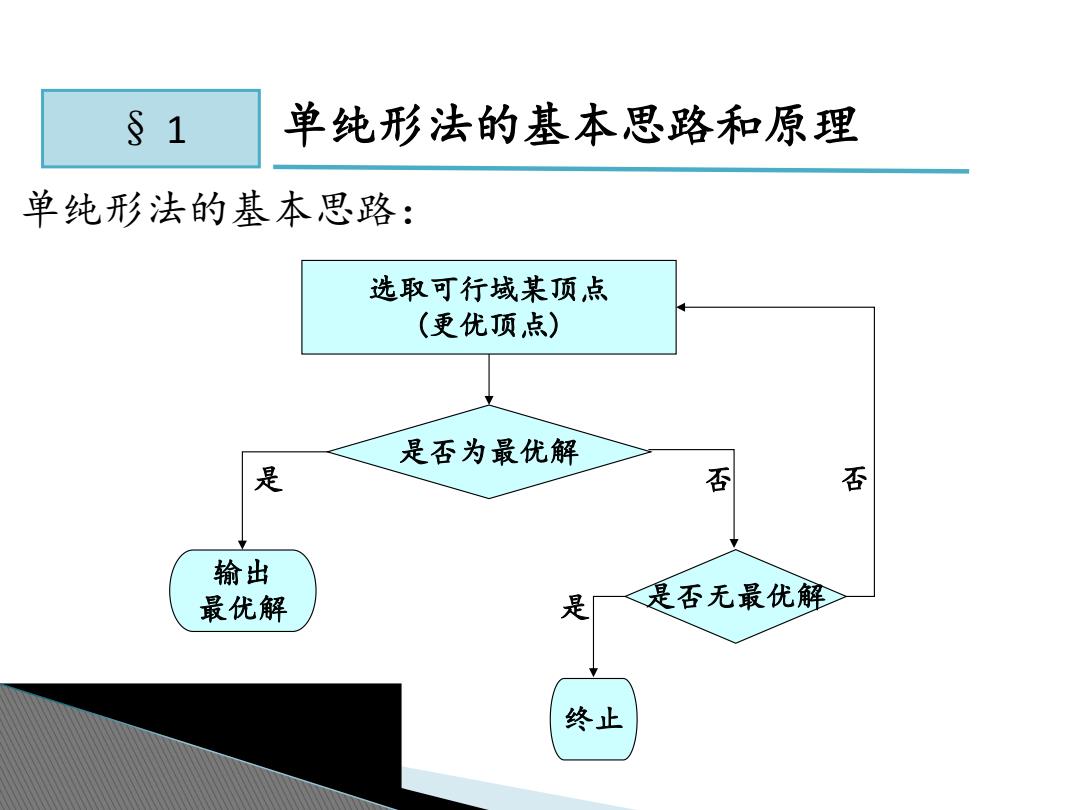
§1 单纯形法的基本思路和原理 单纯形法的基本思路: 选取可行域某顶点 (更优顶点) 是否为最优解 是 否 否 输出 最优解 是 <是否无最优解 终止
§ 1 单纯形法的基本思路和原理 单纯形法的基本思路: 是 否 选取可行域某顶点 (更优顶点) 是否为最优解 输出 最优解 终止 是 是否无最优解 否

§1 单纯形法的基本思路和原理 一、 找出一个初始基本可行解 下面通过第二章例1的求解来介绍单纯形法。 在加上松弛变量之后得到此线性规划的标准形式。 目标函数:max50x1+100x2 约束条件:x1+x2+51=300, 2x1+x2+52=400, x2+S3=250, x,≥0(=1,2),S≥0(=1,2,3)
§ 1 单纯形法的基本思路和原理 一 、找出一个初始基本可行解 下面通过第二章例1的求解来介绍单纯形法。 在加上松弛变量之后得到此线性规划的标准形式。 目标函数:max 50x1+100x2 约束条件:x1+x2+s1=300, 2x1+x2+s2=400, x2+s3=250, xi ≥0(i=1,2),sj≥0(j=1,2,3)

§1 单纯形法的基本思路和原理 该线性规划问题约束方程的系数矩阵为: 711100 A=(p1,P2,P3,P4,P)=21 010 01001 其中卫,为系数矩阵A第j列的向量.A的秩为3,方程 组变量个数大于A的秩,从方程组的无数组解中找一 个初始可行解
§ 1 单纯形法的基本思路和原理 该线性规划问题约束方程的系数矩阵为: 其中 pj为系数矩阵 A 第 j 列的向量.A 的秩为3,方程 组变量个数大于 A 的秩,从方程组的无数组解中找一 个初始可行解。 1 2 3 4 5 1 1 1 0 0 ( , , , , ) 2 1 0 1 0 0 1 0 0 1 A p p p p p

§1 单纯形法的基本思路和原理 如何找初始基本可行解? 基本概念 基 AmXn是约束条件系数矩阵,秩为m。若BmXm是A的子阵, 且可逆,称B为一个基。 基向量 基B中的一列即称为一个基向量。 非基 向量 在A中除了基B之外的一列称之为基B的非基向量。 基变量 与基向量p;相应的变量x,叫基变量,基变量有m个。 非基 变量 与非基向量p相应的变量x叫非基变量,非基变量有n-m个
§ 1 单纯形法的基本思路和原理 基 Am×n 是约束条件系数矩阵,秩为 m。若 Bm×m 是 A 的子阵, 且可逆,称 B 为一个基。 如何找初始基本可行解? 基本概念 基向量 基 B 中的一列即称为一个基向量。 非基 向量 在 A 中除了基 B 之外的一列称之为基 B 的非基向量。 基变量 与基向量 pi 相应的变量 xi 叫基变量,基变量有m个。 非基 变量 与非基向量 pj 相应的变量 xj叫非基变量,非基变量有n‒m 个

§1 单纯形法的基本思路和原理 若在约束方程组系数矩阵中找到一个基,令其非 基变量为零,再求解该m元线性方程组可得到唯一 解,该解称之为线性规划的基本解。 此例题找到A的一个基B,(可逆子阵): 110 B=10 101 0,约束方程变为基变量的方程
§ 1 单纯形法的基本思路和原理 此例题找到 A 的一个基 B3(可逆子阵): 令非基变量 x1=0 ,s2=0 , 约束方程变为基变量的方程。 3 1 1 0 1 0 0 1 0 1 B 若在约束方程组系数矩阵中找到一个基,令其非 基变量为零,再求解该 m 元线性方程组可得到唯一 解,该解称之为线性规划的基本解

§1 单纯形法的基本思路和原理 基变量的约束方程: x2+S1=300, x2=400, x2+53=250, 求解得到此线性规划的一个基本解: x=0,x=400,S1=-100,S2=0,S3=-150
§ 1 单纯形法的基本思路和原理 基变量的约束方程: x2+s1=300, x2=400, x2+s3=250, 求解得到此线性规划的一个基本解: x1=0,x2=400,s1=−100,s2=0,s3=−150

§1 单纯形法的基本思路和原理 由于该基本解中 S1=-100,53=-150, 不满足决策变量非负的约束条件,不是可行解。 满足非负条件的基本解叫做基本可行解, 并把这样的基叫做可行基
§ 1 单纯形法的基本思路和原理 由于该基本解中 s1=−100,s3=−150 , 不满足决策变量非负的约束条件,不是可行解。 满足非负条件的基本解叫做基本可行解, 并把这样的基叫做可行基
§1 单纯形法的基本思路和原理 一般来说判断一个基是否是可行基,只有在求出 其基本解以后。 能否在求解之前,找到一个可行基呢? 也就是能否找到的一个基保证在求解之 后得到的解一定是基本可行解呢?
§ 1 单纯形法的基本思路和原理 一般来说判断一个基是否是可行基,只有在求出 其基本解以后。 能否在求解之前,找到一个可行基呢? 也就是能否找到的一个基保证在求解之 后得到的解一定是基本可行解呢?