
管理运筹学 第八章目标规划
管理运筹学 第八章 目标规划
本章内容 ㄖ 目标规划问题举例 有优先权的目标规划的图解法 3 复杂情况下的有优先权的目标规划 加权目标规划
目标规划问题举例 有优先权的目标规划的图解法 复杂情况下的有优先权的目标规划 加权目标规划 本章内容 1 2 3 4

§1 目标规划问题举例 例1企业生产 不同企业的生产目标是不同的。但随着环境问题的日益突出, 可持续发展已成为全社会必须考虑的问题。因此,企业生产 必须承担起社会责任,考虑环境污染、社会效益、公众形象 等多个方面。 例2商务活动 企业在进行盈亏平衡预算时,不能只集中在一种产品上,需 要用多产品的盈亏分析来解决具有多个盈亏平衡点的决策问 题(多产品的盈亏平衡点往往是不一致的)
§ 1 目标规划问题举例 例2 商务活动 企业在进行盈亏平衡预算时,不能只集中在一种产品上,需 要用多产品的盈亏分析来解决具有多个盈亏平衡点的决策问 题(多产品的盈亏平衡点往往是不一致的)。 例1 企业生产 不同企业的生产目标是不同的。但随着环境问题的日益突出, 可持续发展已成为全社会必须考虑的问题。因此,企业生产 必须承担起社会责任,考虑环境污染、社会效益、公众形象 等多个方面

§1 目标规划问题举例 例3投资 企业投资时不仅仅要考虑收益率,还要考虑风险。通常,风险 大的投资收益率更高。因此,企业管理者只有在对收益率和风 险承受水平有明确的期望值时,才能得到满意的决策。 例4裁员 企业裁员时要考虑很多可能彼此矛盾的因素。裁员的首要目的 是压缩人员开支,但忠诚度就很难保证,员工的心理压力、工作 压力等都会增加,可能产生负面影响。 例5营销 营销方案的策划和执行存在多个目标。既希望能达到立竿见影 成本控制在某一个范围内
§ 1 目标规划问题举例 例3 投资 企业投资时不仅仅要考虑收益率,还要考虑风险。通常,风险 大的投资收益率更高。因此,企业管理者只有在对收益率和风 险承受水平有明确的期望值时,才能得到满意的决策。 例4 裁员 企业裁员时要考虑很多可能彼此矛盾的因素。裁员的首要目的 是压缩人员开支,但忠诚度就很难保证,员工的心理压力、工作 压力等都会增加,可能产生负面影响。 例5 营销 营销方案的策划和执行存在多个目标。既希望能达到立竿见影 的效果,又希望营销的成本控制在某一个范围内
本章内容 目标规划问题举例 有优先权的目标规划的图解法 复杂情况下的有优先权的目标规划 加权目标规划
目标规划问题举例 有优先权的目标规划的图解法 复杂情况下的有优先权的目标规划 加权目标规划 本章内容 1 2 3 4
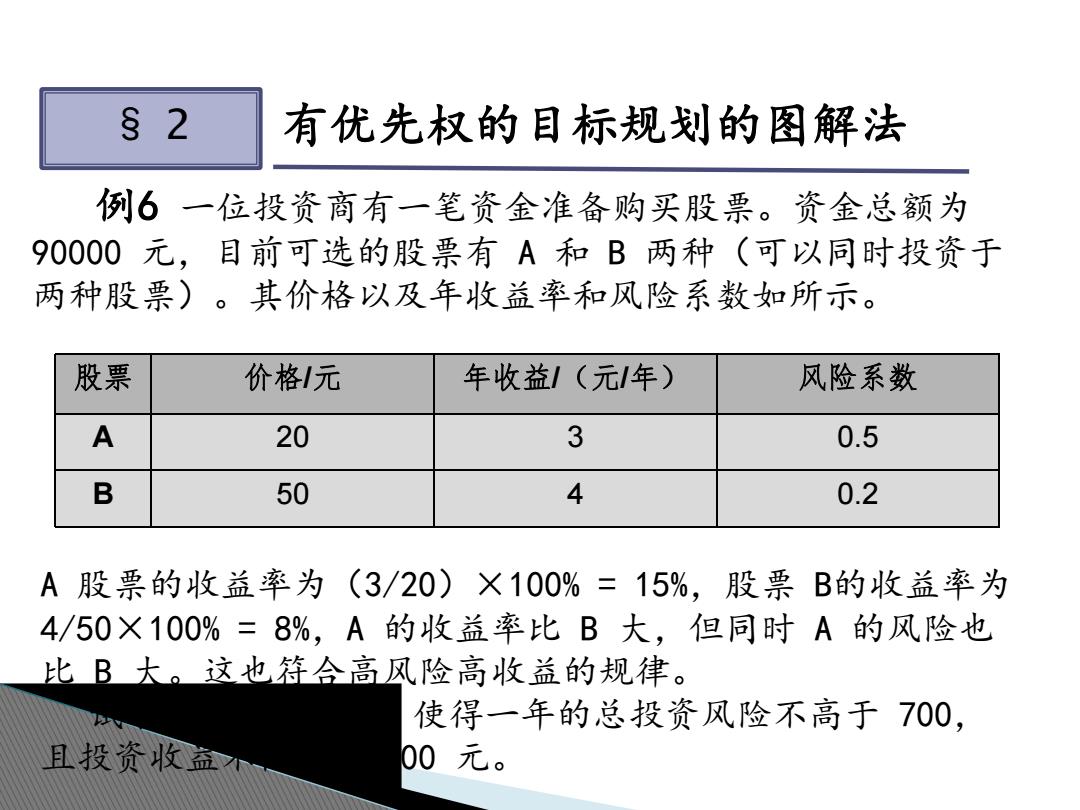
§2 有优先权的目标规划的图解法 例6一位投资商有一笔资金准备购买股票。资金总额为 90000元,目前可选的股票有A和B两种(可以同时投资于 两种股票)。其价格以及年收益率和风险系数如所示。 股票 价格1元 年收益/(元年) 风险系数 A 20 3 0.5 B 50 4 0.2 A股票的收益率为(3/20)X100%=15%,股票B的收益率为 4/50X100%=8%,A的收益率比B大,但同时A的风险也 比B大。这也符合高风险高收益的规律。 使得一年的总投资风险不高于700, 且投资收益 00元
§ 2 有优先权的目标规划的图解法 例6 一位投资商有一笔资金准备购买股票。资金总额为 90000 元,目前可选的股票有 A 和 B 两种(可以同时投资于 两种股票)。其价格以及年收益率和风险系数如所示。 股票 价格/元 年收益/(元/年) 风险系数 A 20 3 0.5 B 50 4 0.2 A 股票的收益率为(3/20)×100% = 15%,股票 B的收益率为 4/50×100% = 8%,A 的收益率比 B 大,但同时 A 的风险也 比 B 大。这也符合高风险高收益的规律。 试求一种投资方案,使得一年的总投资风险不高于 700, 且投资收益不低于 10000 元

§2 有优先权的目标规划的图解法 两个目标变量:限制风险、确保收益。 假设目标限制风险的优先权比目标确保收益大,必须首先满足 第一个目标,再尽量满足第二个目标。 建立模型: 设X1、X2分别表示投资商所购买的A股票和B股票的数量。 资金总额的约束:总投资额不能高于90000元。即 20x1+50x2≤90000。 注意:资产总额的约束是刚性约束,是不允许突破的
§ 2 有优先权的目标规划的图解法 两个目标变量:限制风险、确保收益。 假设目标限制风险的优先权比目标确保收益大,必须首先满足 第一个目标,再尽量满足第二个目标。 建立模型: 设 x1、x2 分别表示投资商所购买的 A 股票和 B 股票的数量。 资金总额的约束:总投资额不能高于 90000 元。即 20x1 + 50 x2≤90000。 注意:资产总额的约束是刚性约束,是不允许突破的

§2 有优先权的目标规划的图解法 一、 约束条件 风险约束:总风险不能超过700。投资的总风险0.5x1+ 0.2x2。引入两个变量d+和d1,等式如下。 0.5x1+0.2x2=700+d1+-d1 d+表示总风险高于700的部分,d1表示总风险少于700 的部分,d1*,d1≥0。 把d+和d1这样的变量称为偏差变量。偏差变量的作用是 允许约束条件不被精确满足
§ 2 有优先权的目标规划的图解法 风险约束:总风险不能超过 700。投资的总风险0.5x1 + 0.2x2。引入两个变量 d1 +和 d1−,等式如下。 d1 +表示总风险高于 700 的部分,d1−表示总风险少于 700 的部分,d1 + ,d1− ≥0。 把 d1 +和 d1−这样的变量称为偏差变量。偏差变量的作用是 允许约束条件不被精确满足。 0.5x1 + 0.2x2 =700+ d1 + − d1− 一 、约束条件

§2 目标规划的图解法 等式转换可得 0.5x1+0.2x2-d1++d1=700。 年收入约束: 年收入=3x1+4x2 引入变量d2*和d2,分别表示年收入超过与低于10000 的数量。 第2个目标可表示为 x2-d2++d2=10000
§ 2 目标规划的图解法 等式转换可得 0.5x1 + 0.2x2 − d1 + + d1− =700。 年收入约束: 年收入=3x1+4x2 引入变量 d2 +和 d2− ,分别表示年收入超过与低于 10000 的数量。 第 2 个目标可表示为 3x1+4x2 − d2 + + d2− =10000

§2 有优先权的目标规划的图解法 二、有优先权的目标函数 本问题中目标较高的优先权为P1,目标较低的优先权为 P20 针对每一个优先权,建立一个单一目标的线性规划模型。 首先建立具有最高优先权的目标的线性规划模型,求解;然 后按优先权逐渐降低的顺序分别建立单一目标的线性规划模 型,方法是在原来模型的基础上修改目标函数,并把原来模 型求解所得的目标最优值作为一个新的约束条件加入到当前 模型中,并求解
§ 2 有优先权的目标规划的图解法 二、有优先权的目标函数 本问题中目标较高的优先权为 P1,目标较低的优先权为 P2。 针对每一个优先权,建立一个单一目标的线性规划模型。 首先建立具有最高优先权的目标的线性规划模型,求解;然 后按优先权逐渐降低的顺序分别建立单一目标的线性规划模 型,方法是在原来模型的基础上修改目标函数,并把原来模 型求解所得的目标最优值作为一个新的约束条件加入到当前 模型中,并求解