
管理运筹学 第七章整数规划
管理运筹学 第七章 整数规划

第七章 整数规划 在整数规划中: 纯整数规划问题:所有变量均为非负整数 0-1规划:变量的取值只限0和1 混合整数规划问题:部分变量为非负整数
第七章 整数规划 在整数规划中: 纯整数规划问题:所有变量均为非负整数 0-1 规划:变量的取值只限 0 和 1 混合整数规划问题:部分变量为非负整数

本章内容 整数规划的图解法 整数规划的计算机求解 整数规划的应用 整数规划的分枝定界法 5 0-1规划的解法
整数规划的图解法 整数规划的计算机求解 整数规划的应用 整数规划的分枝定界法 本章内容 1 2 3 4 5 0-1规划的解法
§1 整数规划的图解法 例1.某公司拟用集装箱托运甲、乙两种货物,这两种货 物每件的体积、重量、可获利润以及托运所受限制如表。 货物 每件体积/立方英尺 每件重量/百千克 每件利润百元 甲 195 4 2 乙 273 40 0 托运限制 1365 140 甲种货物至多托运4件,问两种货物各托运多少件,可 使获得利润最大
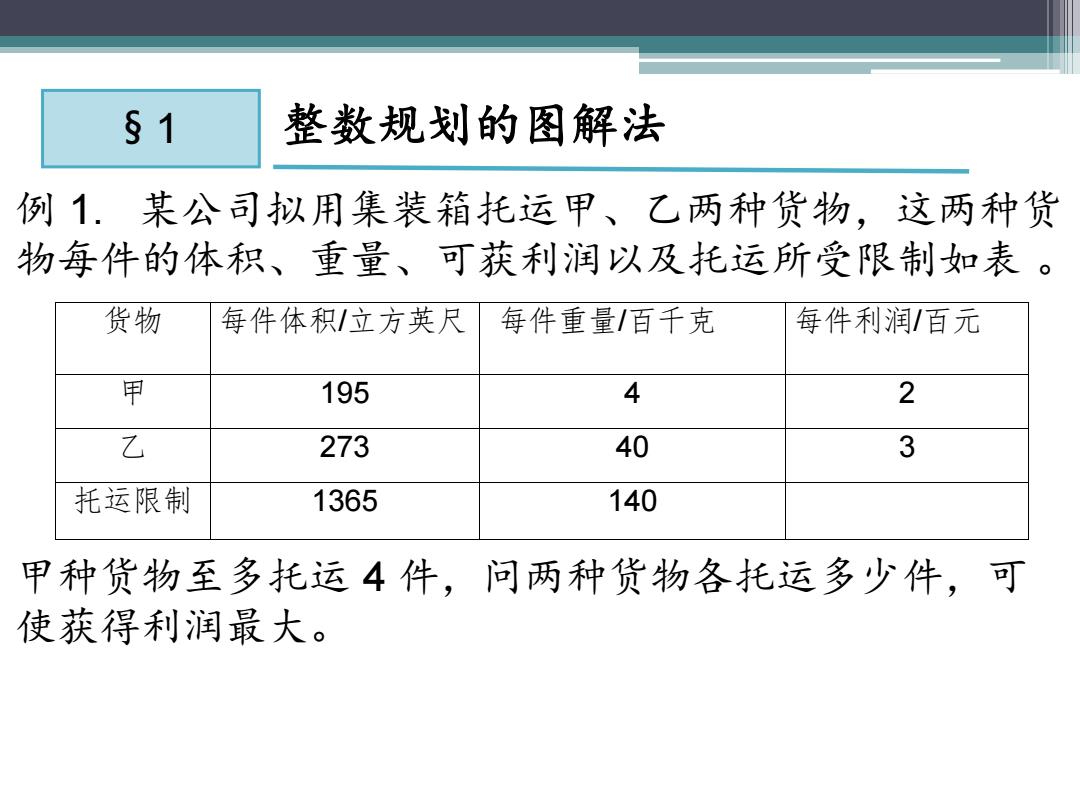
§ 1 整数规划的图解法 例 1. 某公司拟用集装箱托运甲、乙两种货物,这两种货 物每件的体积、重量、可获利润以及托运所受限制如表 。 甲种货物至多托运 4 件,问两种货物各托运多少件,可 使获得利润最大。 货物 每件体积/立方英尺 每件重量/百千克 每件利润/百元 甲 195 4 2 乙 273 40 3 托运限制 1365 140

§1 整数规划的图解法 解:设X1、X2分别为甲、乙两种货物托运的件数,建立 模型 目标函数: max z 2x1 +3X2 约束条件:s.t.195x1+273X2≤1365(体积限制) 4x1+40x2≤140 (重量限制) X1≤4 X1,X2≥0,为整数 去掉最后一个约束,是一个线性规划问题
§ 1 整数规划的图解法 解:设 x1、x2 分别为甲、乙两种货物托运的件数,建立 模型 目标函数: max z = 2x1 +3x2 约束条件: s.t. 195 x1 + 273 x2≤1 365 (体积限制) x1≤4 4x1 + 40x2≤140 (重量限制) x1,x2≥0, 去掉最后一个约束,是一个线性规划问题。 为整数
§1 整数规划的图解法 利用图解法 整数规划的最优解不都镯静最钱x属蝌 解 取九 通过“四舍五入” 66 X2 3 2 2+3x2- 2x1+3x2=14.66 2X1+3X2=14 0 4 X1
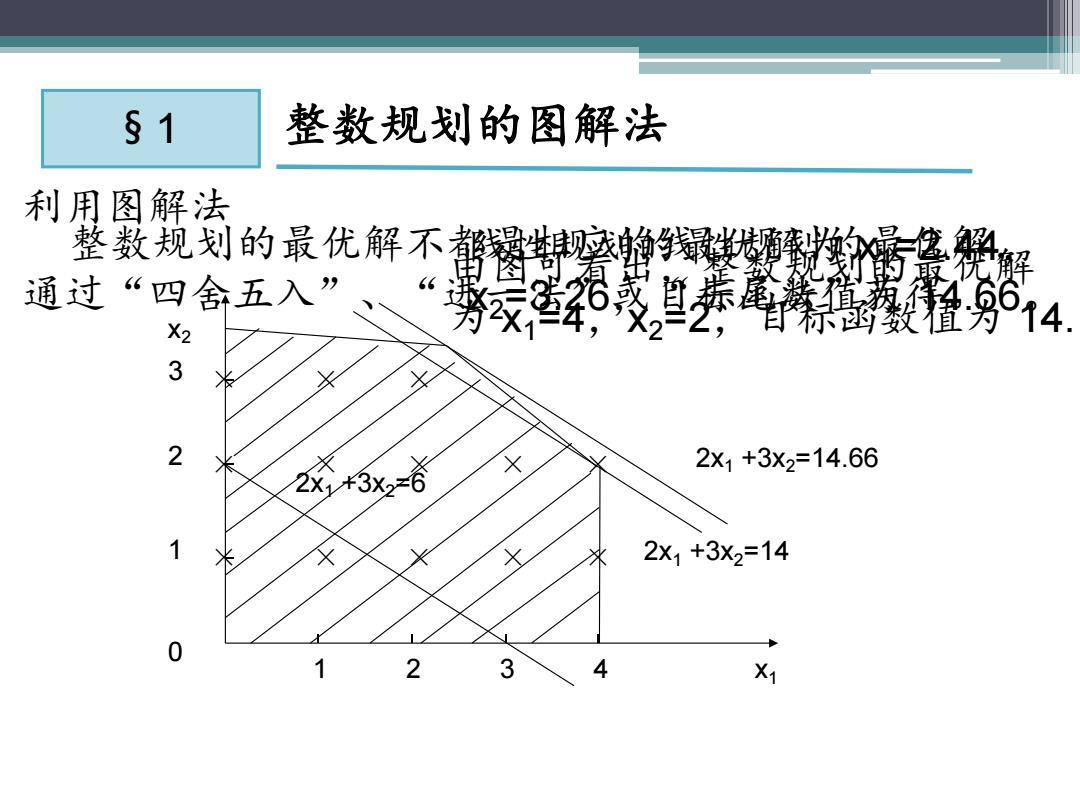
x2 § 1 整数规划的图解法 利用图解法 3 2 1 0 1 2 3 4 x1 2x1 +3x2=6 2x1 +3x2=14.66 2x1 +3x2=14 × × × × × × × × × × × × 线性规划的最优解为 x1=2.44, x2=3.26,目标函数值为 14.66。 由图可看出,整数规划的最优解 为 x1=4,x2=2,目标函数值为 14. × 整数规划的最优解不都是相应的线性规划的最优解, 通过“四舍五入” 、 “进一法”或“去尾法”获得

§1 整数规划的图解法 性质1:任何求最大目标函数值的纯整数规划或混合整 数规划的最大目标函数值小于或等于相应的线性规划的最 大目标函数值; 任何求最小目标函数值的纯整数规划或混合整数规划 的最小目标函数值大于或等于相应的线性规划的最小目标 函数值
§ 1 整数规划的图解法 性质 1:任何求最大目标函数值的纯整数规划或混合整 数规划的最大目标函数值小于或等于相应的线性规划的最 大目标函数值; 任何求最小目标函数值的纯整数规划或混合整数规划 的最小目标函数值大于或等于相应的线性规划的最小目标 函数值

本章内容 整数规划的图解法 2 整数规划的计算机求解 3 整数规划的应用 整数规划的分枝定界法 0-1规划的解法
整数规划的图解法 整数规划的计算机求解 整数规划的应用 整数规划的分枝定界法 本章内容 2 1 3 4 5 0-1规划的解法

§2 整数规划的计算机求解 例2 max Z 3x1 X2 3X3 s.t. -X1+2X2+X3≤4 4x2-3X3≤2 X1-3X2+2X3≤3 X1,X2,X3≥0 X1,X2,X3为整数
§ 2 整数规划的计算机求解 例 2 max z = 3x1 + x2 + 3x3 s.t. −x1 + 2x2 + x3≤4 4x2 −3x3≤2 x1 −3x2 + 2x3≤3 x1 ,x2 ,x3≥0 x1 ,x2 ,x3 为整数
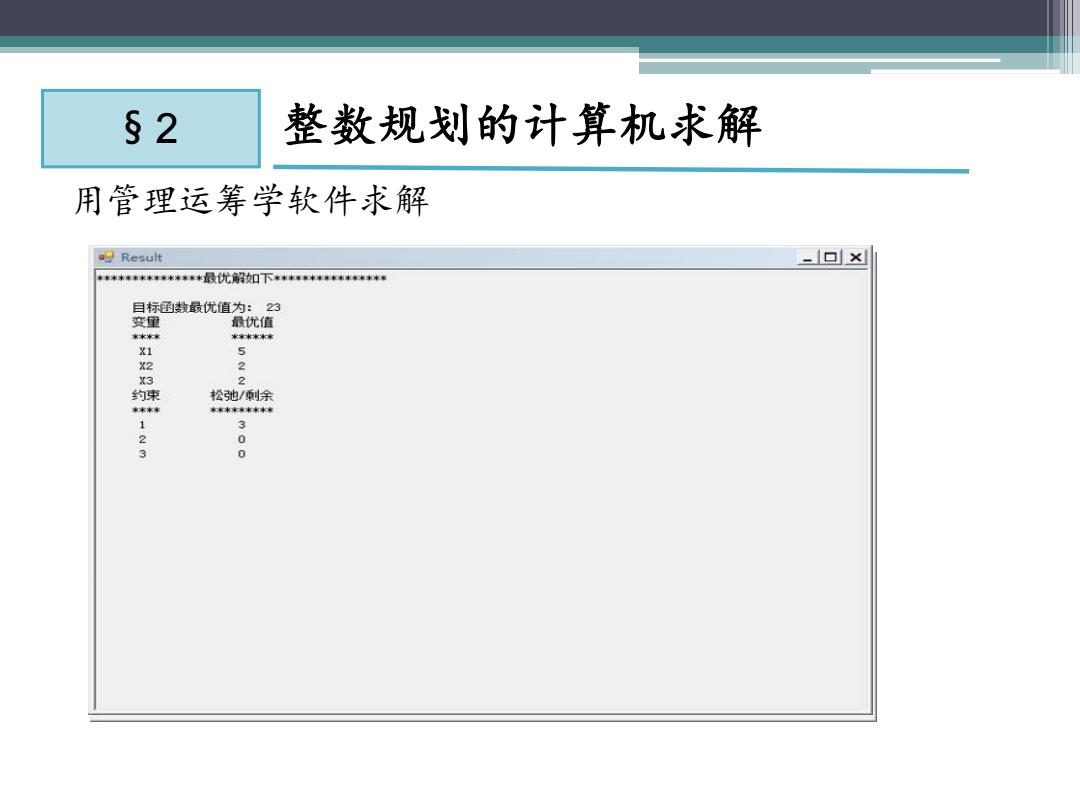
§2 整数规划的计算机求解 用管理运筹学软件求解 明Result -1口x 车*率本****来*最优解如下*水率**水** 目标数最优值为 3 变 最优值 1 5 味 松弛/剩余 123 3
§ 2 整数规划的计算机求解 用管理运筹学软件求解