
管理运筹学 第九章图与网络模型
管理运筹学 第九章 图与网络模型
本章内容 图与网络的基本概念 2 最短路问题 3 最小生成树问题 最大流问题 最小费用最大流问题
1 图与网络的基本概念 2 最短路问题 3 5 4 最小生成树问题 最大流问题 最小费用最大流问题 本章内容
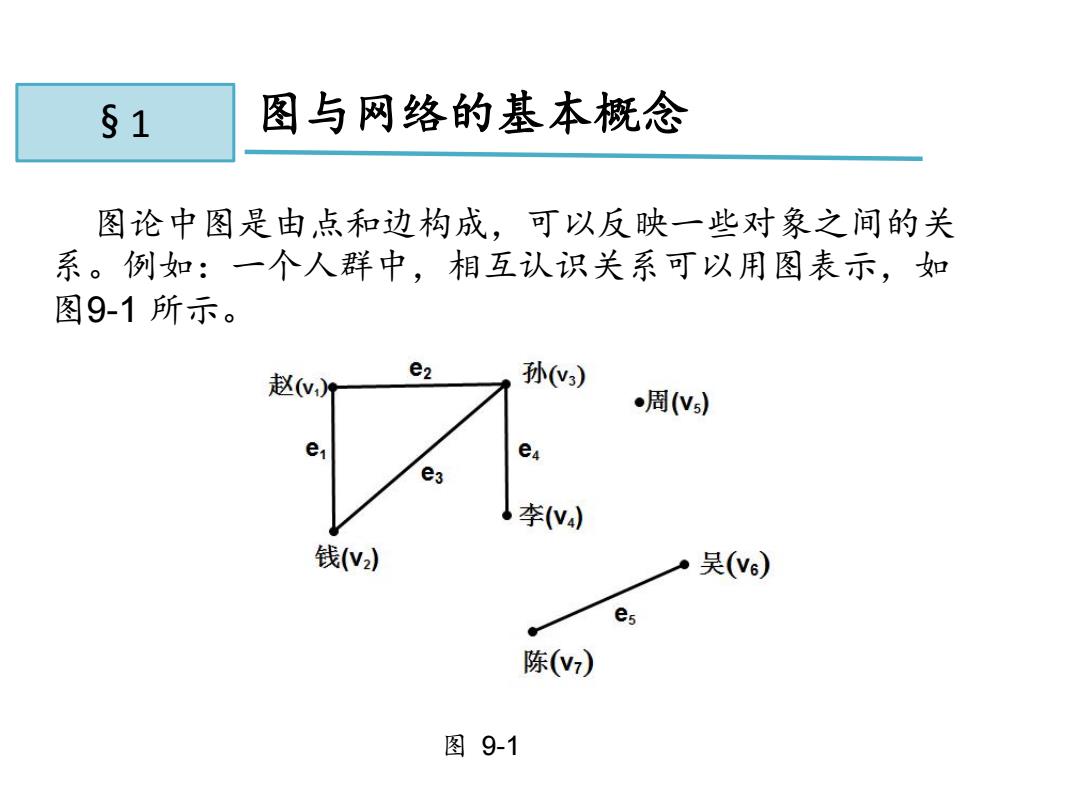
§1 图与网络的基本概念 图论中图是由点和边构成,可以反映一些对象之间的关 系。例如:一个人群中,相互认识关系可以用图表示,如 图9-1所示。 赵(w e2 孙(3) 周(Ns) e e e3 ·李(v 钱(v) ·吴(v6) es 陈(v7) 图9-1
图论中图是由点和边构成,可以反映一些对象之间的关 系。例如:一个人群中,相互认识关系可以用图表示,如 图9-1 所示。 11.1 图与网络的基本概念 图 9-1 § 1
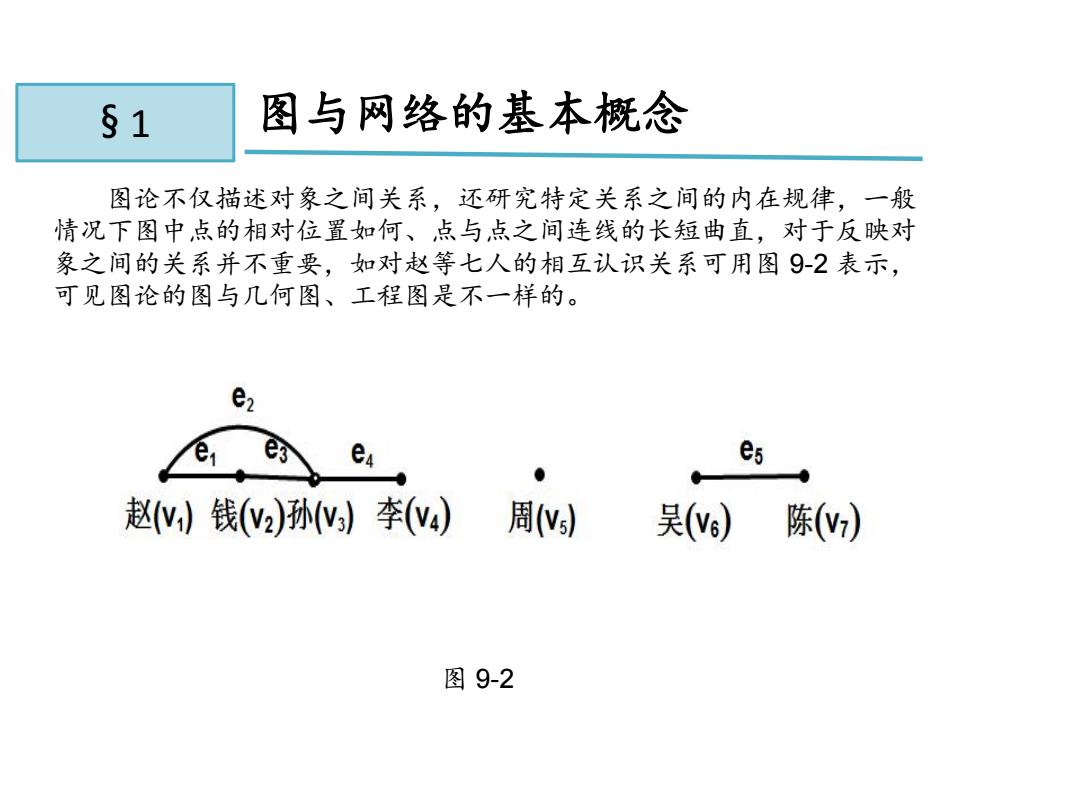
§1 图与网络的基本概念 图论不仅描述对象之间关系,还研究特定关系之间的内在规律,一般 情况下图中点的相对位置如何、点与点之间连线的长短曲直,对于反映对 象之间的关系并不重要,如对赵等七人的相互认识关系可用图9-2表示, 可见图论的图与几何图、工程图是不一样的。 e e, es ● 赵)钱(2)孙)李(4) 周) 吴() 陈v) 图9-2
11.1 图与网络的基本概念 图 9-2 § 1 图论不仅描述对象之间关系,还研究特定关系之间的内在规律,一般 情况下图中点的相对位置如何、点与点之间连线的长短曲直,对于反映对 象之间的关系并不重要,如对赵等七人的相互认识关系可用图 9-2 表示, 可见图论的图与几何图、工程图是不一样的
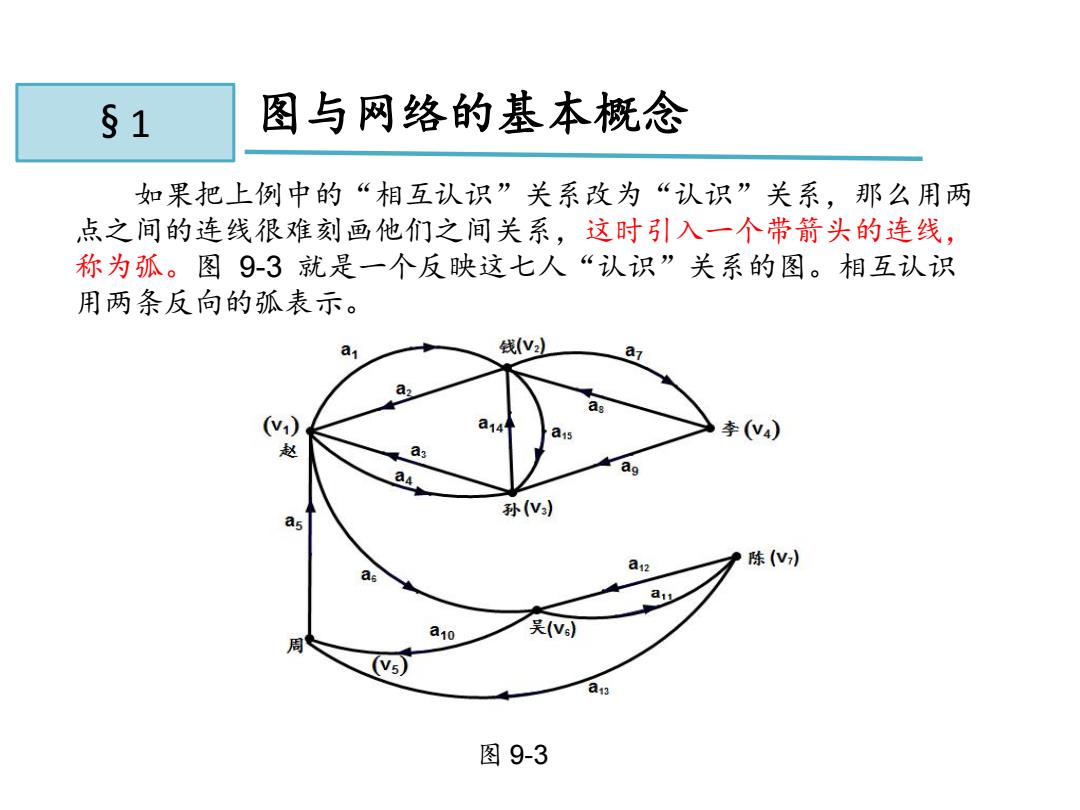
§1 图与网络的基本概念 如果把上例中的“相互认识”关系改为“认识”关系,那么用两 点之间的连线很难刻画他们之间关系,这时引入一个带箭头的连线, 称为孤。图9-3就是一个反映这七人“认识”关系的图。相互认识 用两条反向的孤表示。 a 钱V a g (v) 李(V4) 赵 a a 孙(V) 陈(V) as a10 吴(N) N5) 图9-3
如果把上例中的“相互认识”关系改为“认识”关系,那么用两 点之间的连线很难刻画他们之间关系,这时引入一个带箭头的连线, 称为弧。图 9-3 就是一个反映这七人“认识”关系的图。相互认识 用两条反向的弧表示。 11.1 图与网络的基本概念 图 9-3 § 1

§1 图与网络的基本概念 无向图: 点和边构成的图,记作G=(V,曰。 有向图: 点和弧构成的图,记作D=(V,A)。 连通图: 对无向图G,若任何两个不同的点之间,至少存在一条链,则G为 连通图。 回路: 若路的第一个,点和最后一个点相同,则该路为回路。 赋权图: 对无向图G的每一条边(,),相应有一个数W,则称图G为赋权 图,w称为边(Vy)上的权。 网络: 在赋权的有向图D中指定一点,称为发点(记为V),指定另一点为 收点(记为),其余点称为中间点,并把D中的每一条弧的赋权数C 称为孤(,V的容量,这样的赋权有向图D称为网络
11§.11 图与网络的基本概念 无向图: 点和边构成的图,记作 G =(V, E)。 有向图: 点和弧构成的图,记作 D =(V, A)。 连通图: 对无向图 G,若任何两个不同的点之间,至少存在一条链,则 G 为 连通图。 回路: 若路的第一个点和最后一个点相同,则该路为回路。 赋权图: 对无向图 G 的每一条边(vi,vj),相应有一个数 wij,则称图 G 为赋权 图,wij 称为边(vi,vj)上的权。 网络: 在赋权的有向图 D 中指定一点,称为发点(记为 vs),指定另一点为 收点(记为 vt),其余点称为中间点,并把 D 中的每一条弧的赋权数 cij 称为弧(vi,vj)的容量,这样的赋权有向图 D 称为网络
本章内容 图与网络的基本概念 最短路问题 最小生成树问题 最大流问题 最小费用最大流问题
1 图与网络的基本概念 2 最短路问题 3 5 4 最小生成树问题 最大流问题 最小费用最大流问题 本章内容

§2 最短路问题 ◆最短路问题:对一个赋权的有向图D中的指定的两个点V。和V:找到 一条从V到的路,使这条路上所有孤弧的权数的总和最小,这条路被 称之为从V到V,的最短路。这条路上所有孤的权数的总和被称为从V 到V的距离。 ◆求解最短路的Dijkstra算法(双标号法) ◆步骤: 1.给出点V1以标号(0,S) 2.找出已标号的点的集合I,没标号的点的集合J及孤的集合 {(%,V)I∈1,V∈J} 3.如果上述孤的集合是空集,则计算结束。如果V,已标号(,k),则V。到 M的距离为,而从V到V:的最短路径,则可以从V反向追踪到起点 Vs而得到。如果V:未标号,则可以断言不存在从V。到V的有向路。 如果上述的孤的集合不是空集,则转下一步。 4.对上述孤的集合中的每一条孤,计算S=+C0在所有的S中,找 到其值为最小的孤。不妨设此孤为(V),则给此孤的终点以双标号 (Sca,C),返回步骤2
11.2 最短路问题 u 最短路问题:对一个赋权的有向图 D 中的指定的两个点 vs 和 vt 找到 一条从 vs 到vt 的路,使这条路上所有弧的权数的总和最小,这条路被 称之为从 vs 到 vt 的最短路。这条路上所有弧的权数的总和被称为从 vs 到 vt 的距离。 u 求解最短路的 Dijkstra 算法(双标号法) u 步骤: 1.给出点 v1 以标号(0,s) 2.找出已标号的点的集合 I,没标号的点的集合 J 及弧的集合 {(vi , v j ) | vi ∈ I , v j ∈ J } 3.如果上述弧的集合是空集,则计算结束。如果 vt 已标号(l t,kt),则 vs 到 vt 的距离为 l t,而从 vs 到 vt 的最短路径,则可以从 vt 反向追踪到起点 vs 而得到。如果 vt 未标号,则可以断言不存在从 vs 到 vt 的有向路。 如果上述的弧的集合不是空集,则转下一步。 4.对上述弧的集合中的每一条弧,计算 sij = l i + cij。在所有的 sij 中,找 到其值为最小的弧。不妨设此弧为(vc ,vd ),则给此弧的终点以双标号 (scd ,c),返回步骤 2。 § 2
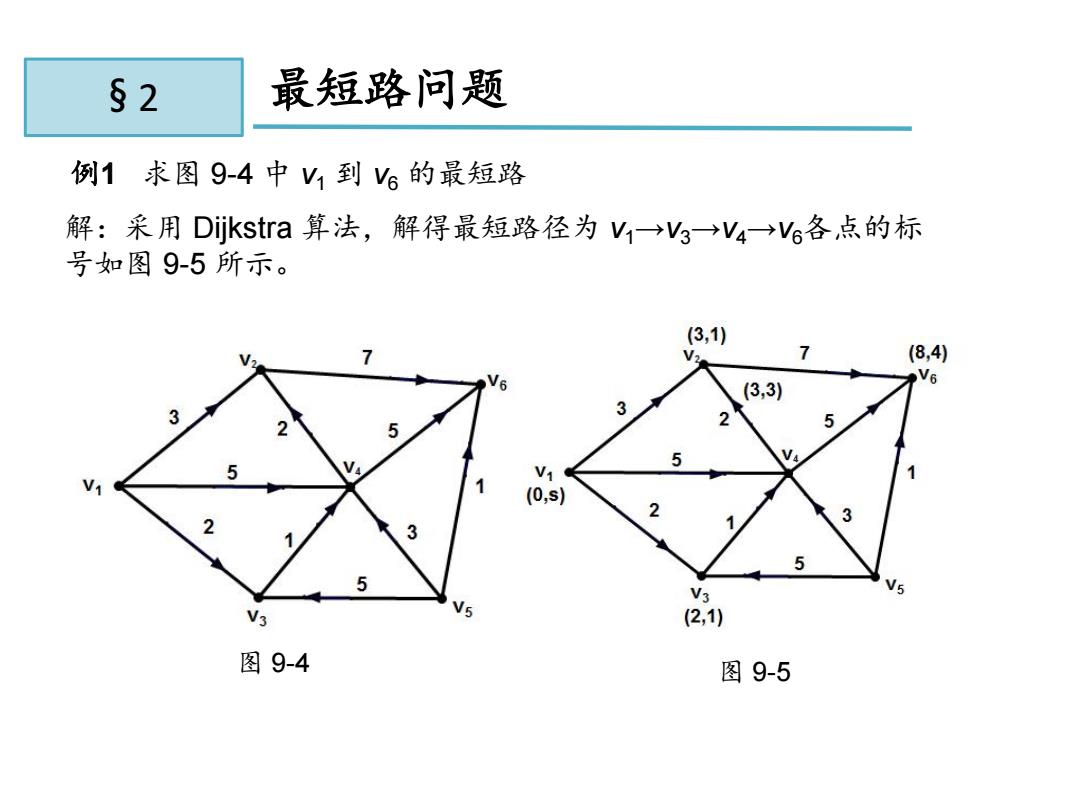
§2 最短路问题 例1求图9-4中V1到V6的最短路 解:采用Dijkstra算法,解得最短路径为V1→Vg→V4→Vs各点的标 号如图9-5所示。 (3,1) N (8,4) N6 V6 (3,3) 3 2 5 5 5 V1 (0,s) V3 V3 V (2,1) 图9-4 图9-5
11.2 最短路问题 例1 求图 9-4 中 v1 到 v6 的最短路 解:采用 Dijkstra 算法,解得最短路径为 v1→v3→v4→v6各点的标 号如图 9-5 所示。 图 图 9-5 9-4 § 2

§2 最短路问题 求解过程如下: (1)给定起始点V1标以(0,S),表示从V1到V1的距离为0,1为起始点。 (2)这时已标定点集合={,未标定点的集合={2,⅓,V4,Vs,6},孤集合(y,V)y ∈1,V,∈J}={(1,2),(1,g),(,V4)},则有min(s12,S13,S14)=S13=2,这样,给 孤(V,V3)的终点3标以(2,1),表示从1到V3的距离为2. (3)这时1={V1,,J={2,V4,V5,%},则min(S12,S14,S34)=S12=S34=3。给孤(V, 2)的终点2标以(3,1),表示从1到2的距离为3;我们给孤(3,V4)的终点V4 标以(3,3),表示从V1到V4的距离为3. (4)这时1={W1,2,V3,V4},J={Ws,%},则有min(S26,s46)=S46=8,这样给点V6标以 (8,4),表示从V1到V6的距离是8. (5)这时I={1,2,V3,V4,%,J={5},而孤集合为空,计算结束。也即5还未 标号,说明从V1到5没有有向路, (6)得到一组最优结果。从终点V%的标号倒推到起点V1,得到此最短路径为V1-V3 V4V6·
11.2 最短路问题 求解过程如下: (1)给定起始点 v1 标以(0,s),表示从 v1 到 v1 的距离为 0,v1 为起始点。 (2)这时已标定点集合 I={v1 },未标定点的集合 J={v2 ,v3 ,v4 ,v5 ,v6 },弧集合{(vi , v j ) |vi ∈ I , v j ∈ J } = {(v1 , v2 ), (v1 , v3 ), (v1 , v4 )} , 则有 min(s12 , s13 , s14 )=s13=2,这样,给 弧( v1 , v3 ) 的终点 v3 标以(2,1),表示从 v1 到 v3 的距离为 2. (3)这时 I = {v1 , v3 }, J = {v2 , v4 , v5 , v6 } ,则min(s12 ,s14 ,s34 )=s12=s34=3。给弧 ( v1 , v2 ) 的终点 v2 标以 (3,1),表示从 v1 到 v2 的距离为 3;我们给弧 ( v3 , v4 ) 的终点 v4 标以 (3,3),表示从 v1 到 v4 的距离为 3. (4)这时 I = {v1 , v2 , v3 , v4 }, J = {v5 , v6 } ,则有 min (s26 ,s46 )=s46=8,这样给点 v6 标以 (8,4),表示从 v1 到 v6 的距离是 8. (5)这时 I = {v1 , v2 , v3 , v4 , v6 }, J = {v5 } ,而弧集合为空,计算结束。也即 v5 还未 标号,说明从 v1 到 v5 没有有向路. (6)得到一组最优结果。从终点 v6 的标号倒推到起点 v1,得到此最短路径为 v1 - v3 - v4 - v6 . § 2