
管理运筹学 第五章单纯形法的灵敏度分析与对偶
管理运筹学 第五章 单纯形法的灵敏度分析与对偶

本章内容 1 单纯形表的灵敏度分析 2 线性规划的对偶问题 3 对偶规划的基本性质 4 对偶单纯形法种特殊情况
单纯形表的灵敏度分析 线性规划的对偶问题 对偶规划的基本性质 对偶单纯形法种特殊情况 本章内容 1 2 3 4

§1 单纯形表的灵敏度分析 一、 目标函数中变量系数Ck灵敏度分析Ck→Ck+△Ck 1、在最终的单纯形表里,x是非基变量 >由于进行行初等变换,约束方程增广矩阵不变 >基变量系数cB不变 zi=CB'Pj >都不变,包括k Ck→Ck+△Ck Ok=Ck-Zk Ck+△Ck-2k=Ok十△Ck ok+AC:≤0
§ 1 单纯形表的灵敏度分析 一 、目标函数中变量系数 ck 灵敏度分析 1、在最终的单纯形表里,xk是非基变量 Ø由于进行行初等变换,约束方程增广矩阵不变 Ø基变量系数cB不变 Øzj都不变,包括zk j B j z c p k k k c c c k k c 0 k k c k k k k k k k k c z c c z c k k k c c c 若要原来的最优解不变

§1 单纯形表的灵敏度分析 2.在最终的单纯形表中,x是基变量 >由于进行行初等变换,约束方程增广矩阵不变 >基变量系数c变化 >对所有的z都变化,包括z
§ 1 单纯形表的灵敏度分析 2.在最终的单纯形表中,xk 是基变量 Ø由于进行行初等变换,约束方程增广矩阵不变 Ø基变量系数cB变化 Ø对所有的zj都变化,包括zk j B j z c p 假设cB =(cB1 , cB2 ,…, ck ,…,cBm ) (cB1 , cB2 ,…, ck+ck ,…,cBm )
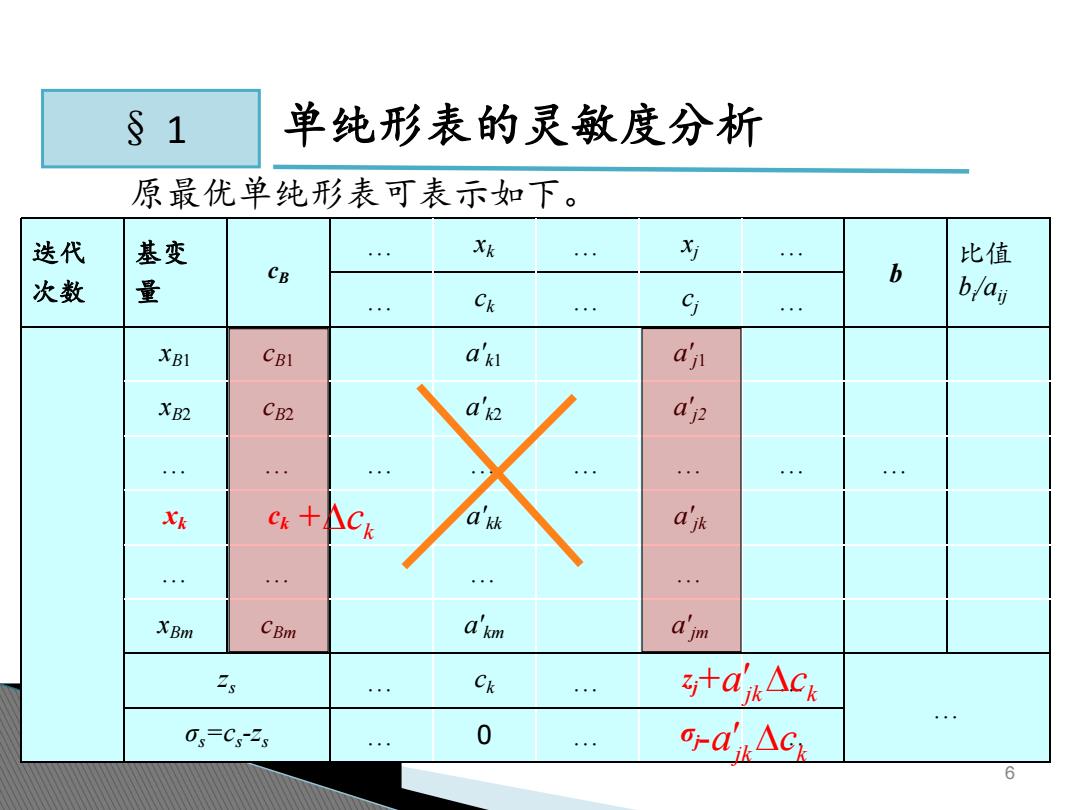
§1 单纯形表的灵敏度分析 原最优单纯形表可表示如下。 迭代 基变 X 5 比值 CB b 次数 量 Ck S b/ai XBI CBI a'k aj XB2 CB2 d'2 a 式k c+Ck a a'jk XBm CBm a'km djm Ck 汁a△ck 0,=C-2g 0 o-dAck 6
6 § 1 原最优单纯形表可表示如下。 单纯形表的灵敏度分析 迭代 次数 基变 量 cB … xk … xj … b 比值 bi … c /aij k … cj … xB1 cB1 a' k1 a' j1 xB2 cB2 a' k2 a' j2 … … … … … … … … xk ck a' kk a' jk … … … … xBm cBm a' km a' jm zs … ck … zj … … σs=cs-zs … 0 … σj … + k c + jk k a c - jk k a c

§1 单纯形表的灵敏度分析 CB(CB1,Ca2,…,Ck,,CBm)(CBI,CB2,,C+△ck,…,CBn) 2)=CB1a+CB2a2,+…+(ck+ACx)a%+…+CBma =z,+△Cxa 由于0,=9一 -0-Aciay
§ 1 单纯形表的灵敏度分析 cB =(cB1 , cB2 ,…, ck ,…,cBm ) (cB1 , cB2 ,…, ck+ck ,…,cBm ) 1 1 2 2 ( ) = j B j B j k k kj Bm m j j k kj z c a c a c c a c a z c a ( ) = j j j j j k kj j k kj c z c z c a c a 由于σj = cj- zj

§1 单纯形表的灵敏度分析 若要最优解不变 ag>0→Ac≥ Gj=0j-Ackay a%0好scmm,<0
§ 1 单纯形表的灵敏度分析 0 0 0 j kj k kj j j kj k kj a c a a c a 当j≠k时, 当j=k时, 0, 1 = 0 = k k kk x k k k k a k k k k k kk c c z c c z c a 为基变量 max{ 0} min{ 0} j j kj k kj kj kj a c a a a j = j k kj c a 若要最优解不变
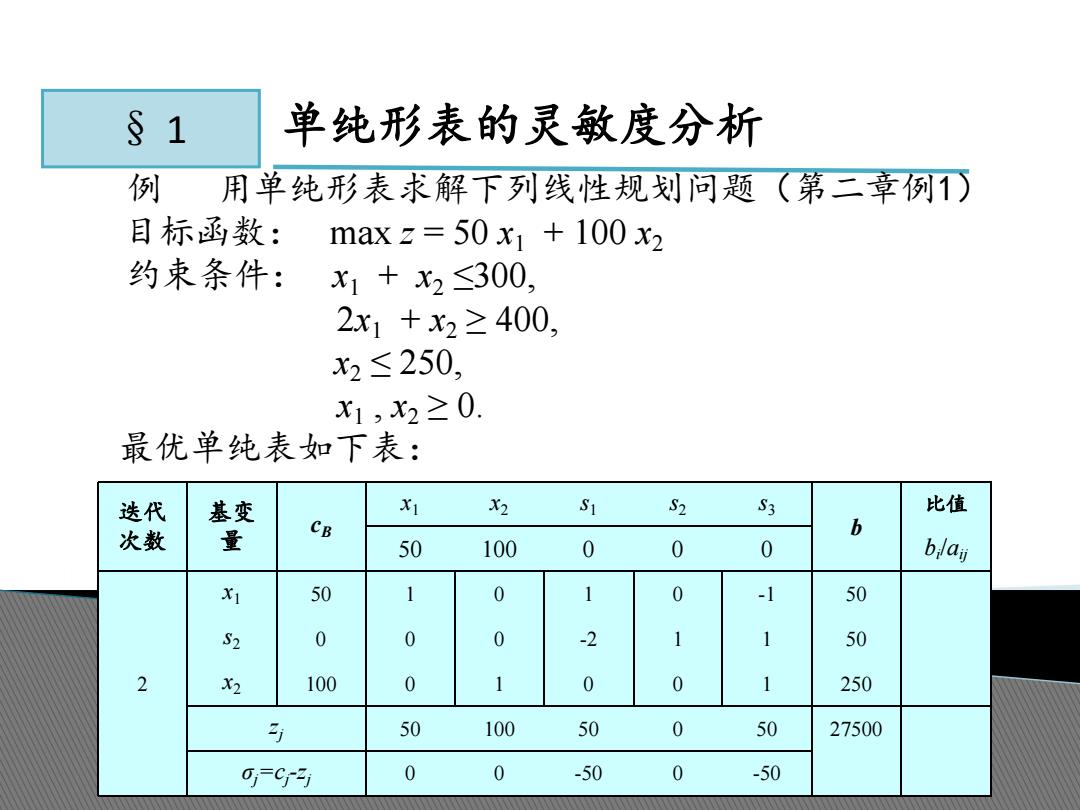
§1 单纯形表的灵敏度分析 例 用单纯形表求解下列线性规划问题(第二章例1) 目标函数: maxz=50x1+100x2 约束条件: x1+x2≤300, 2x1+x2≥400, x2≤250, x1,x2≥0 最优单纯表如下表: 迭代 基变 X1 X2 S1 S2 S3 比值 次数 量 CB 50 100 0 0 0 blaj X1 50 1 0 0 -1 50 0 0 0 1 50 X2 100 0 1 0 0 1 250 j 50 100 50 0 50 27500 01=C 0 0 -50 0 -50
§ 1 单纯形表的灵敏度分析 例 用单纯形表求解下列线性规划问题(第二章例1) 目标函数: max z = 50 x1 + 100 x2 约束条件: x1 + x2 ≤300, 2x1 + x2 ≥ 400, x2 ≤ 250, x1 , x2 ≥ 0. 最优单纯表如下表: 迭代 次数 基变 量 cB x1 x2 s1 s2 s3 b 比值 50 100 0 0 0 bi/aij 2 x1 50 1 0 1 0 -1 50 s2 0 0 0 -2 1 1 50 x2 100 0 1 0 0 1 250 zj 50 100 50 0 50 27500 σj=cj-zj 0 0 -50 0 -50
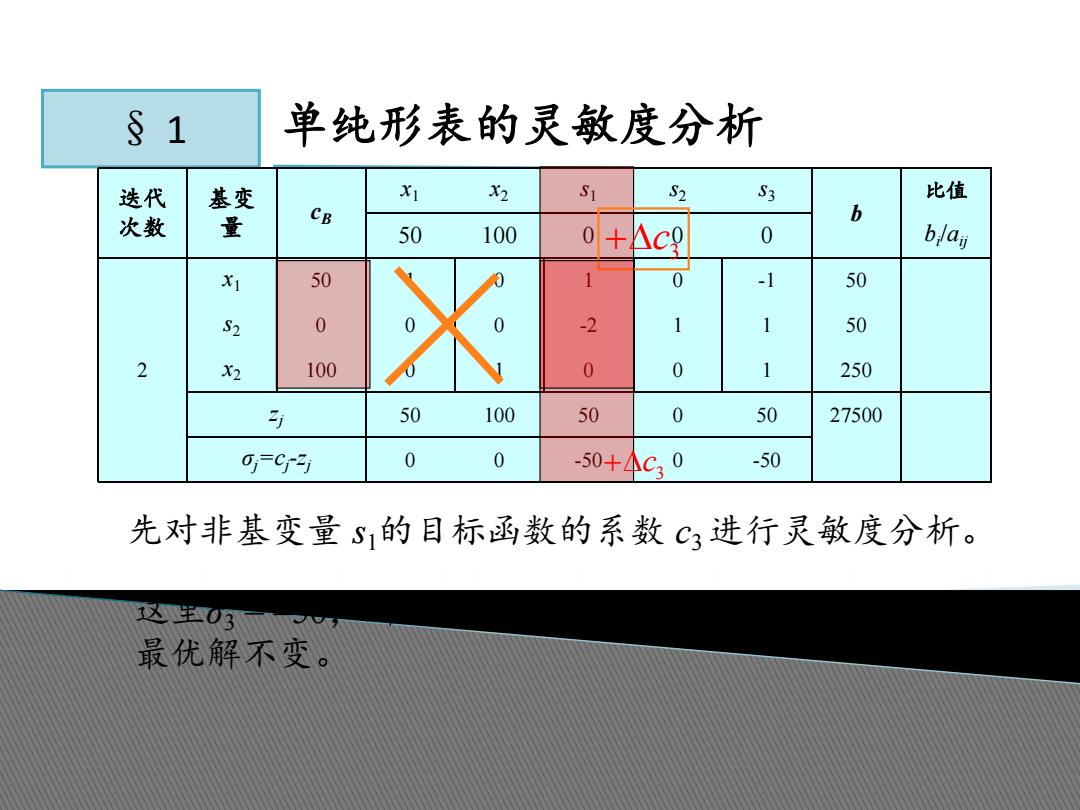
§1 单纯形表的灵敏度分析 迭代 基变 X1 X2 S1 S3 比值 次数 量 CB b 50 100 0+ Ac 0 blaj 50 1 0 -1 50 0 1 50 2 X2 100 0 0 0 1 250 50 100 50 0 50 27500 0=C 0 0 -50+4C30 -50 先对非基变量S,的目标函数的系数C3进行灵敏度分析。 03 最优解不变
§ 1 单纯形表的灵敏度分析 迭代 次数 基变 量 cB x1 x2 s1 s2 s3 b 比值 50 100 0 0 0 bi/aij 2 x1 50 1 0 1 0 -1 50 s2 0 0 0 -2 1 1 50 x2 100 0 1 0 0 1 250 zj 50 100 50 0 50 27500 σj=cj-zj 0 0 -50 0 -50 先对非基变量 s1的目标函数的系数 c3进行灵敏度分析。 这里σ3 = ‒50,所以当 c3的增量Δ c3 ≤50 时,c' 3 ≤50时, 最优解不变。 3 c 3 c

§1 单纯形表的灵敏度分析 迭代 基变 X2 S1 S2 S3 比值 次数 量 CB 50+4c100 0 0 0 bla 50+ C 0 -1 50 0 1 50 2 100 1 250 50叶△C100 50+△C10 50-497500 0-C 0 0 -50 0 -50 o 0 0 -50 0 -50 -△C +△C 当-50≤△c≤50,即在0≤c1≤100时最优解不变
§ 1 单纯形表的灵敏度分析 当−50≤Δ c1≤50 ,即在 0≤ c1 ′≤100 时最优解不变。 迭代 次数 基变 量 cB x1 x2 s1 s2 s3 b 比值 50 100 0 0 0 bi/aij 2 x1 50 1 0 1 0 -1 50 s2 0 0 0 -2 1 1 50 x2 100 0 1 0 0 1 250 zj 50 100 50 0 50 27500 σj=cj-zj 0 0 -50 0 -50 再对基变量x1的目标函数系数 c1进行灵敏度分析 1 c 1 c j 0 0 1 50 c 0 1 50 c 1 c 1 c 1 c