农业院校《试验设计与分析》课程参考资料（区域试验分析方法）品种区域试验中算术平均值、BLUP和AMMI估值的精度比较.pdf_大学文库

第27卷第4期作物学报 Vol 27.No.4 2001年7月 ACTA AGRONOMICA SINICA Jy,2001 品种区域试验中算术平均值、BLUP和AMMⅡ估值的精度比较张群远！孔繁玲1杨付新2 (中国衣业大学植物遗传有种系，北京100094：2中国农业科学院棉花研究所，河南安阳455112 提要利用1982年以来我国棉花、小麦、水稻和玉米的60套区域试验数据，采用交叉验证方法，对区域试验中算术平均值、最佳线性无偏预测值(bst iner ubased predictor,BP)和AMM(additive main effectsand multiplicative interaction)模型估值的预测精度进行比较，结果表明，与算术平均值相比，AM 估值精度的增益倍数(gain factor,GF)平均为1.045，变幅为0.963-1.414，其精度多数情况下提高不大：UP的GF平均为1.170，变幅为1.008-1.619，其精度普遍较高.同时，文中对3种估值的模型作了论述和比较。关键词区域试验：BLUP:AMM:预测精度 Comparison of the Predictive Accuracy of Arithmetic Means and BLUPs and AMMI Estimates in Regional Crop Trials ZHANG Qun-Yuan'KONG Fan-Ling YANG Fu-Xin (Dpartment of Plant Gmnctics and Breoding China Agricumral Unirersity,Beijing 0094:Instinte f Coton.Chinese Acndemy ofA- griculural Scimce,Anyung 455112.China) Abstract Sixty sets of data from regional trials of cotton,wheat,rice and maize since 1982 in China were used in cross validation to compare the predictive accuracy of arithmetic means and BLUPs(best lin- ear unbiased predictors)and AMMI additive main effects and multiplicative interaction)estimates.The average precision gain factor(GF)of AMMI relative to arithmetic mean was 1.045 with a range from 0. 963 to 1.414,which showed slight increases of precision:BLUP was found commonly to outperform arithmetic mean and AMMI with an average GF of 1.17,ranged from 1.008 to 1.619. Key words Regional Trial:BLUP:AMMI:Predictive Accuracy 作物品种区域试验的目的是在多环境下对参试品种进行比较和评价，以确定新品种的推广价值和适应范围。这种比较和评价有赖于对各品种在各环境下的产量（或其它性状值，统称品种×环境组合均值)作出准确估计。我国区试中历来采用算术平均值进行估计。算术平均值是最为常用的一种估值，虽简便易行，但存在一定局限。一方面，由于算术平均值是直接以样本平均数来估计总体均值，估计时未能充分利用试验中多种变异的信息，要获得准确估值，需较多的重复数：另一方面，算术平均值实质上是对品种试验表现的事后描述，并非国家白燃科学基金资助项目( 0433)。赵虹、王磊、王洁、葛知男和孙世贤同志提供了部分数据，特此致谢：

4期张群远等：品种区域试验中算术平均值、BLUP和AMM估值的精度比较 429 对品种未来表现的预测，而后者是我们真正感兴趣的，具有更重要的实践意义。近年来，国外不少研究表明，利用一些较复杂的模型和方法，可以得到预测精度比算术平均值更高的估值，其中混合线性模型(mixed linear model)的最佳线性无偏预测(best linear unbiased prediction BLUP)i和AMMl(additive main effects and multiplicative interaction)模型的AMM估值2]是最主要的两种。本文结合我国多年区域试验的数据，对算术平均值、BIUP和AMM三种估值的模型和预测精度进行比较，探讨各种方法在我国区试中的适用性，以期有针对性地引入和利用。 1材料和方法 1.1数据资料数据取自我国棉花、小麦、水稻和玉米区试分重复记载的共60年次的历史资料（详见表 1)。其中棉花数据为皮棉产量，小麦、水稻和玉米数据为子粒产量，单位均为kg/hm。 1.2各种估值的模型和计算表1区试数据及其提供单位为便于论述，下面以v个品 Table 1 Data and their providers 种，s个环境（通常是地点或地点× 作物区试组别年份资料提供单位年份的组合环境)，r次重复的区域 T-I 试验为例来阐明各种估值所依据的棉花中国农科院棉数学模型及具体计算方法。第i个长江流域常规棉 90-98 江苏农科料院经作所品种在第j个环境中的第k次重复小麦黄准春水组河南农科院小麦所 87-91 Wheat 黄淮冬水组观测值记为Y。各种估值的计算水稻中早粳晚熟组92,93,96,97,98 就是依据特定模型对Y中的信息中国农科院作物所 Rice 中早粳中熟组 93.94.98 进行处理和提取的过程：而各种模中识敦组 91.94.95.96 中围农科院水稻所玉来化北条玉来型的实质是根据各种假设把Y表 96-98 全国农技推广服务中心西北春玉米 06.g7 达成相应的理论构成。黄淮夏玉米 1.2.1算术平均值用算术平均值来估计各品种在各环境下的性状值，所依据的是统计学上最简单的一种线性模型： Y诚=可十E球 (1) 四为第i个品种在第j个环境中的真实均值，也就是我们要估计的真值：©为第；个品种在第；个环境中的第k次重复观测值的误差。从试验设计的角度看，区试中品种和环境是两个因素，品种i和环境j的搭配即为一个处理，以也就是处理均值。所以，此模型也叫处理均值(treatment means)模型2，它把每个y表示为g加上e的形式，并用算术平均的方法对 g作出估计： g=了写=∑Yg, (2) 了，即为第i个品种在第j个环境中的算术平均值。这一模型十分简单和直观，实际应用中往往不对其作专门说明。 1.2.2最佳线性无偏预测值(BUP)区试中由于方差分析的需要，更常用的是另一种线性可加模型[21：万方数据 Y=μ+g++0g+e (3)

对品种未来表现的预测，而后者是我们真正感兴趣的，具有更重要的实践意义。近年来，国外不少研究表明，利用一些较复杂的模型和方法，可以得到预测精度比算术平均值更高的估值，其中混合线性模型（!"#$% &"’$() !*%$&）的最佳线性无偏预测（+$,- &"’$() .’+"(,$% /)$%"0-"*’， 1234）［5］和 677（8 (%%"-"9$ !("’ $::$0-, (’% !.&-"/&"0(-"9$ "’-$)(0-"*’）模型的 6778 估值［;］是最主要的两种。本文结合我国多年区域试验的数据，对算术平均值、1234 和 6778 三种估值的模型和预测精度进行比较，探讨各种方法在我国区试中的适用性，以期有针对性地引入和利用。 ! 材料和方法 5 年次的历史资料（详见表 5）。其中棉花数据为皮棉产量，小麦、水稻和玉米数据为子粒产量，单位均为 ?@ A B!;。表 ! 区试数据及其提供单位 "#$%& ! ’#(# #)* (+&,- .-/0,*&-1 作物 C)*/, 区试组别 D)"(& @)*./, 年份 E$(), 资料提供单位 /)*9"%$), *: %(-( 棉花黄河流域春棉 F; G H= 中国农科院棉花所 C*--*’ 黄河流域夏棉 F= G HI 中国农科院棉花所长江流域常规棉 H> G HF 江苏农科院经作所小麦 JB$(- 黄淮春水组黄淮冬水组 FK G H5 河南农科院小麦所水稻 L"0$ 中早粳晚熟组中早粳中熟组 H;，HI，H=，HK，HF HI，HM，HF 中国农科院作物所中籼迟熟组 H5，HM，HN，H= 中国农科院水稻所玉米华北春玉米 H= G HF 全国农技推广服务中心 7("O$ 西北春玉米 H=，HK 黄淮夏玉米 H= !<2 各种估值的模型和计算为便于论述，下面以 9 个品种，, 个环境（通常是地点或地点 P 年份的组合环境），) 次重复的区域试验为例来阐明各种估值所依据的数学模型及具体计算方法。第 " 个品种在第 Q 个环境中的第 ? 次重复观测值记为 !"#$。各种估值的计算就是依据特定模型对 !"#$中的信息进行处理和提取的过程；而各种模型的实质是根据各种假设把 !"#$表达成相应的理论构成。 5<;<5 算术平均值用算术平均值来估计各品种在各环境下的性状值，所依据的是统计学上最简单的一种线性模型： !"#$ % !"# &""#$ （5） !"# 为第 " 个品种在第 Q 个环境中的真实均值，也就是我们要估计的真值；""#$为第 " 个品种在第 Q 个环境中的第 ? 次重复观测值的误差。从试验设计的角度看，区试中品种和环境是两个因素，品种 " 和环境 Q 的搭配即为一个处理，!"# 也就是处理均值。所以，此模型也叫处理均值（-)$(-!$’- !$(’,）模型［;］；它把每个 !"#$表示为!"# 加上""#$的形式，并用算术平均的方法对 !"# 作出估计： ’ !"# % !!"# % " ( $ % 5 !"#$ ) ( （;） !!"# 即为第 " 个品种在第 Q 个环境中的算术平均值。这一模型十分简单和直观，实际应用中往往不对其作专门说明。 5<;<; 最佳线性无偏预测值（1234）区试中由于方差分析的需要，更常用的是另一种线性可加模型［;］： !"#$ % ! & *" & +# &#"# &""#$ （I） M 期张群远等：品种区域试验中算术平均值、1234 和 6778 估值的精度比较 M;H 万方数据

430 作物学报 :为所有观测值所属总体的均值：g:为品种i的效应：g为环境j的效应：日为品种i与环境j的基因型×环境(GE)互作效应：同(1)式。区试中往往根据这一模型来进行方差分析。这一模型实质上是把(1)式模型中的进一步分解为4、g、g和四种构成，此时，为四种效应的一个可估函数（即四者之和）：利用更一般的线性模型求解方法，可以获得，的最佳线性无偏估值(best linear unbiased estimation,,BLUE)或最佳线性无偏预测值(BLUP)y。在模型求解之前，首先要对各种效应是随机还是固定作出假设。“固定”意味着该效应值在试验中是一系列定值：“随机”则是指试验中该效应的一系列值是来自于具有特定均值和方差的总体的一个随机样本。一般来说，u是固定效应，e是随机效应，g:、e和，则可根据实际情况作出各种假设，所以，(3)式往往是一个既有固定效应，又有随机效应的混合线性模型。在的四种构成均为固定效应时，其估值为BUE:在四种构成中含有随机效应时，由于不再是一个严格意义上的参数，故其估值称为预测值，即BLUP。Peipho(1994口曾在Henderson (1975)3]基础上推导出平衡数据时各种模型下4的BUE或BUP的计算公式如下：模型I:g、e和0均为固定效应：的估值记为BLUE: BLUE =Y+(Yi-Y)+(Yj-Y)+(Yi-Yi-Yi+Y)=Yi (4a) 模型Ⅱ：号和0，均为随机效应：g的估值记为BLUPge BLUPge Y+h (Yi -Y)+h.(Y -Y)+h(Yi -Yi-Y+Y) 4h) 模型Ⅲ：e为固定效应，g:和，为随机效应：g的估值记为BLUPg BLUPg Y+hg(Yi-Y)+(Yi-Y)+he(Yii -Yi-Yi+Y) 4c) 模型IN:g为固定效应，e和0g为随机效应：g的估值记为BLUPe。. BLUPe=了+(Y-了)+h.(y-)+h(Yg-Y:-y+了) (4d) 其中： GTE+SOT hg=g2/r+o证+o元 (5a h:=g2/r+G证+to (5b) hge=g2/r+证 (5c) 以上各式中，了为试验总均值：了为第i个品种的试验均值：了为第j个环境的试验均值：了，同(2)式：2、2、和σ证分别为误差、品种、环境以及品种×环境互作的方差：均衡数据时，可以按一定模型假设进行方差分析，通过求解期望均方组成来估计这些方差值4]。用这些方差估值代替真值后得出的结果，虽然已不再是严格的BP,但习惯上仍称之为 BLUP。根据(4a)式可看出，算术平均值其实就是固定模型下的BLUE。由(4)入、(4e)和(4d)式不难看出，BP实质是依据随机效应方差和误差方差的大小，相应减小了随机效应在4：估值中所占的比例，对算术平均值作了适当的“收缩”。模型Ⅱ和Ⅲ中把品种效应g:看作随机的，这似乎与我们区试中方差分析时通常采取的品种效应固定的习惯做法有所矛盾。事实上，只要品种效应值服从一定的概率总体的分布，即使试验方案中品种并非随机抽取，依据特定的分析目的，在统计上也可作为随机效应看待山。就实际含义来看，(5a)式意味着，若试验误差据，对试验中表现越极端的品种（即了：一了的绝对值越大），越应该持“谨慎

!为所有观测值所属总体的均值；!" 为品种 ! 的效应；#$ 为环境 " 的效应；""$ 为品种 ! 与环境 " 的基因型 # 环境（$%）互作效应；#"$%同（&）式。区试中往往根据这一模型来进行方差分析。这一模型实质上是把（&）式模型中的!"$ 进一步分解为!、!"、#$ 和""$四种构成，此时，!"$ 为四种效应的一个可估函数（即四者之和）；利用更一般的线性模型求解方法，可以获得!"$ 的最佳线性无偏估值（’()* +!,(-. /,’!-)(0 ()*!1-*!2,，345%）或最佳线性无偏预测值（3456）［7］。在模型求解之前，首先要对各种效应是随机还是固定作出假设。“固定”意味着该效应值在试验中是一系列定值；“随机”则是指试验中该效应的一系列值是来自于具有特定均值和方差的总体的一个随机样本。一般来说，!是固定效应，#"$%是随机效应，!"、#$ 和""$ 则可根据实际情况作出各种假设，所以，（7）式往往是一个既有固定效应，又有随机效应的混合线性模型。在!"$ 的四种构成均为固定效应时，其估值为 345%；在四种构成中含有随机效应时，由于!"$不再是一个严格意义上的参数，故其估值称为预测值，即 3456。6(!89（2 &::;）［&］曾在）［7］基础上推导出平衡数据时各种模型下!"$ 的 345% 或 3456 的计算公式如下：模型!：!"、#$ 和""$ 均为固定效应；!"$ 的估值记为 345%； 345% & !’ (（!’" )!’）(（!’$ )!’）(（!’"$ )!’" )!’$ (!’）& !’"$ （;-）模型"：!"、#$ 和""$ 均为随机效应；!"$ 的估值记为 3456?(； 3456?( & !’ ( *（! !’" )!’）( *（# !’$ )!’）( *! （# !’"$ )!’" )!’$ (!’）（;’）模型#：#$ 为固定效应，!" 和""$ 为随机效应；!"$ 的估值记为 3456?。 3456? & !’ ( *（! !’" )!’）(（!’$ )!’）( *! （# !’"$ )!’" )!’$ (!’）（;@）模型$：!" 为固定效应，#$ 和""$ 为随机效应；!"$ 的估值记为 3456(。 3456( & !’ (（!’" )!’）( *（# !’$ )!’）( *! （# !’"$ )!’" )!’$ (!’）（;0）其中： *! & $A +, ( $- A + $A . / ($A +, ( $- A + （>-） *# & $A +, ( 0 $A , $A . / ($A +, ( 0 $A , （>’） *!# & $A +, $A . / ($A +, （>@）以上各式中，!’ 为试验总均值；!’" 为第 ! 个品种的试验均值；!’$ 为第 " 个环境的试验均值；!’"$ 同（A）式；$A、$A +、$A , 和$A +,分别为误差、品种、环境以及品种 # 环境互作的方差；均衡数据时，可以按一定模型假设进行方差分析，通过求解期望均方组成来估计这些方差值［;］。用这些方差估值代替真值后得出的结果，虽然已不再是严格的 3456，但习惯上仍称之为 3456。根据（;-）式可看出，算术平均值其实就是固定模型下!"$ 的 345%。由（;’）、（;@）和（;0）式不难看出，3456 实质是依据随机效应方差和误差方差的大小，相应减小了随机效应在!"$估值中所占的比例，对算术平均值作了适当的“收缩”。模型"和#中把品种效应 !" 看作随机的，这似乎与我们区试中方差分析时通常采取的品种效应固定的习惯做法有所矛盾。事实上，只要品种效应值服从一定的概率总体的分布，即使试验方案中品种并非随机抽取，依据特定的分析目的，在统计上也可作为随机效应看待［&］。就实际含义来看，（>-）式意味着，若试验误差$A 越大，对试验中表现越极端的品种（即!’" B!’ 的绝对值越大），越应该持“谨慎” ;7C 作物学报 A= 卷万方数据

4期张群远等：品种区域试验中算术平均值、BLUP和AMM估值的精度比较 431 态度（即了：-了的“缩小”越多），这与我们的实际经验是吻合的。所以，品种随机的假设在此有其合理性。 1.2.3AMMI模型及其估值对模型(3)中的互作效应值0进行主成分分解(principal com ponent analysis,PCA),即得到AMI模型[2： Yg=以+哥+与+n+P作+g (6) 入。为品种×环境两向互作值矩阵的第n个奇异值（其平方即为特征根）：um为互作值矩阵中品种i的特征向量的第n个元素：n为互作值矩阵中环境j的特征向量的第n个元素：P 为O,进行PCA分解后的剩余部分：p的最大可取值N为s和v中的最小值减I,即p≤N=Mim (s-1,v-1)。p的取值不同，(6)式可得到不同的模型，所以，AI模型其实是一系列模型的总称。p取值从到N,对应模型分别称为AMM-O、AMM-1、AMM-2·AMM-N模型。实际应用中往往根据F测验的显著性来确定p的大小（一般取入值较大的前1~3项），这时，P 以后的(N-p)个PCA项被当作剩余归入Pg中。AMMI模型中的P被当作误差看待，所以，品种 ×环境组合均值的AMM组成为： =r+8+9+xa (7) 由于AMMI模型把各种效应看作是固定的，所以，与(4a)式同理，(7)式中的u、g:和e 分别以2=了，g:=(了-了)和g=(了-下)进行估计：入m、un和n则需先求出互作值矩阵a =了，-了：-了+了，再作特征分解求得它们的估值。最后得到的AMl估值为 ANNI(g)=了+了-了+i (8) AMI模型在保留模型(3)加性主效部分的同时，利用PCA方法压缩简化了互作的信息。理论上讲，这有助于剔除算术平均值中所包含的部分误差，从而提高以估值的精度。需要指出的是，当AMI模型的p取最大值N时（此时称为AMM全模型），模型中乘式互作项总和与 (3)式中的0，一致，所以，此时AMM(g)与(5a)式的BLUE(g)以及算术平均值相等 1.3各种估值精度的交叉验证各种估值精度的比较采用交叉验证(cross validation)方法2]。具体做法是，对每年的区试数据(v个品种，s个地点，r次重复)，以试点为单位，把r个重复观测值随机分开，其中r1 个用于建立模型和估计，（称为建模数据），剩余1个用于验证（称为验证数据）。利用建模数据，根据(4)组式和(8)式，分别求出g的BLUE、BLUPge、BLUPg BLUPe和AMMI估值（算术平均值即B心E,故不再单独计算)：由于本文使用的是平衡数据，(5)组式中的各种方差成分直接通过方差分析的方法获得。对于每种估值，先根据(9)式出计算相应的平均预测差平方和(mean square prediction differences,MSPD),然后根据(1O)式求出该估值相对于算术平均值的精度增益倍数(gain factor,GF)。 MsPD=∑(Y,-￥与P/s (9) i=1j=1 MSe GF=(T-1)(MSPD-Me） (10) 公式中Y为品种i在环境j上的估计值：Y为验证观测值：MS为环境内的误差项均方，由全部观侧值的号差分析获得。重复进行300次数据分样和计算，得到每种估值的平均

态度（即!!" !!! 的“缩小”越多），这与我们的实际经验是吻合的。所以，品种随机的假设在此有其合理性。 "#$#% &’’( 模型及其估值对模型（%）中的互作效应值!"#进行主成分分解（)*+,-+)./ -012 )0,3,4 .,./56+6，78&），即得到 &’’( 模型［$］： !"#$ % " & ’" & (# & " ) * % " #*+"*,#* &$"# &%"#$ （9） #* 为品种 : 环境两向互作值矩阵的第 , 个奇异值（其平方即为特征根）；+"*为互作值矩阵中品种 + 的特征向量的第 , 个元素；,#*为互作值矩阵中环境 ; 的特征向量的第 , 个元素；$"# 为!"# 进行 78& 分解后的剩余部分；) 的最大可取值 ’+, （6 ! "，= ! "）。) 的取值不同，（9）式可得到不同的模型，所以，&’’( 模型其实是一系列模型的总称。) 取值从到 !!，- ’" >（!!" !!!）和 - (# >（!!# !!!）进行估计；#*、+"*和 ,#*则需先求出互作值矩阵!- "# >!!"# !!!" !!!# D!!，再作特征分解求得它们的估值。最后得到""# 的 &’’( 估值为： &’’（( ""# ）% !!" &!!# .!! & " ) * % " #- * - +"* - ,#* （E） &’’( 模型在保留模型（%）加性主效部分的同时，利用 78& 方法压缩简化了互作的信息。理论上讲，这有助于剔除算术平均值中所包含的部分误差，从而提高""#估值的精度。需要指出的是，当 &’’( 模型的 ) 取最大值 < 时（此时称为 &’’( 全模型），模型中乘式互作项总和与（%）式中的!"# 一致，所以，此时 &’’（( ""# ）与（F.）式的 GHIJ（""# ）以及算术平均值相等。 !#" 各种估值精度的交叉验证各种估值精度的比较采用交叉验证（-*066 =./+K.4+0,）方法［$］。具体做法是，对每年的区试数据（= 个品种，6 个地点，* 次重复），以试点为单位，把 * 个重复观测值随机分开，其中 *2" 个用于建立模型和估计"（"# 称为建模数据），剩余 " 个用于验证（称为验证数据）。利用建模数据，根据（C）组式和（E）式，分别求出""# 的 GHIJ、GHI7L3、GHI7L、GHI73 和 &’’( 估值（算术平均值即 GHIJ，故不再单独计算）；由于本文使用的是平衡数据，（F）组式中的各种方差成分直接通过方差分析的方法获得［C］。对于每种估值，先根据（M）式出计算相应的平均预测差平方和（13., 6NO.*3 )*3K+-4+0, K+PP3*3,-36，’Q7R），然后根据（"?）式求出该估值相对于算术平均值的精度增益倍数（L.+, P.-40*，S@）。 ’Q7R % " , " % " " / # % " （ - !"# . !0 "# ）$ 1 ,/ （M） S@ % ’Q3 （2 . "）（’Q7R ! ’Q3）（"?）公式中 - !"# 为品种 + 在环境 ; 上的估计值；!0 "# 为验证观测值；’Q3 为环境内的误差项均方，由全部观测值的方差分析获得。重复进行 %??? 次数据分样和计算，得到每种估值的平均 C 期张群远等：品种区域试验中算术平均值、GHI7 和 &’’( 估值的精度比较 C%" 万方数据

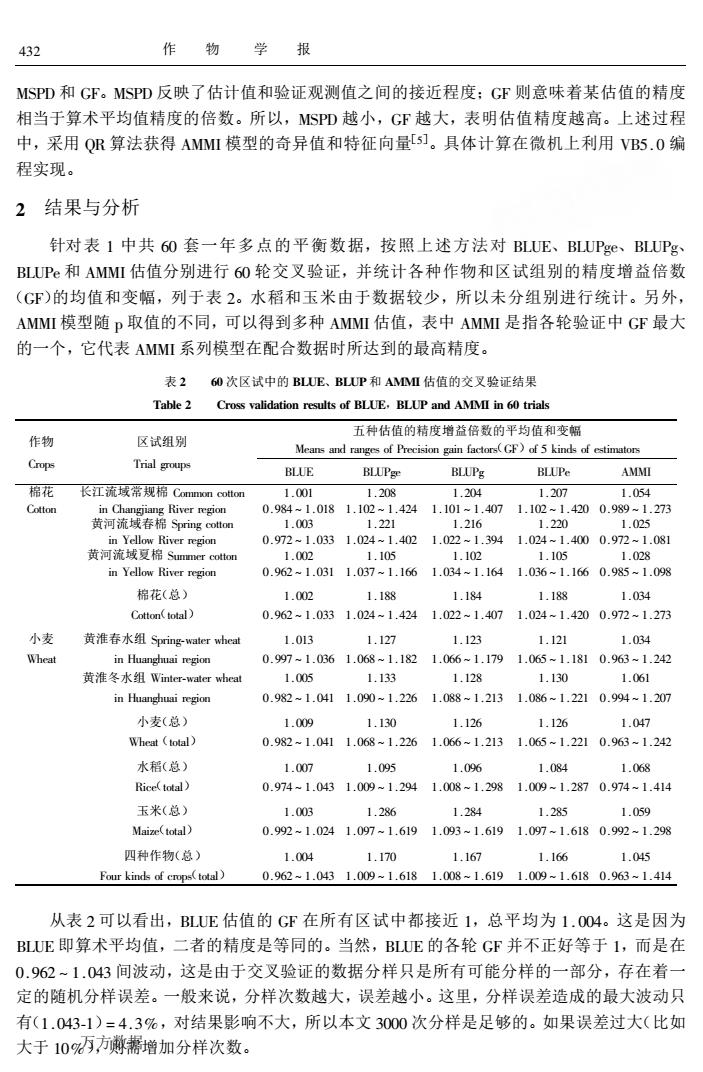
432 作物学报 MSPD和GF。MSPD反映了估计值和验证观测值之间的接近程度：GF则意味着某估值的精度相当于算术平均值精度的倍数。所以，MSD越小，GF越大，表明估值精度越高。上述过程中，采用QR算法获得ANMI模型的奇异值和特征向量s。具体计算在微机上利用VB5.0编程实现 2结果与分析针对表1中共6O套一年多点的平衡数据，按照上述方法对BLUE、BLUPge、BLUPg BLUPe和AMMI估值分别进行6O轮交叉验证，并统计各种作物和区试组别的精度增益倍数 (GF)的均值和变幅，列于表2。水稻和玉米由于数据较少，所以未分组别进行统计。另外， AMMI模型随p取值的不同，可以得到多种AMMI估值，表中AMMI是指各轮验证中GF最大的一个，它代表AMM系列模型在配合数据时所达到的最高精度。表2 0次区试中的BUE、BLUP和AMMI估值的交叉验证结果 Table 2 Cross validation results of BLUE.BLUP and AMMI in 60 trials 作物五种估值的精度增益倍数的平均值和变幅风试组别 Meams and rauges of Prerision gain factors(GF)of 5 kinds of estimators Crops Trial goup BLUE BLUPg BLUPe 长江流域常规棉Comnon cotton 001 .208 1.204 1.20 1.054 黄河流城春棉 0.98 81.24411026 m1.1 4200.9 .27 .03 0.972-1.0331.024-1.4021.02-1.3941.024-1.4000.972-1.081 .102 1.09% 棉花（总） 1.002 1.188 1.184 118 1.034 CoonotaD 0.9621.0331.024-1.4241.022-1.4071.024-1.4200.972-1.273 小麦黄准春水组Sing-water wheat 1.013 1.127 1.123 1.121 1.034 Wheat 0.997-1.0361.068-1.1821.066-1.1791.06-1.1810.963-1.242 黄淮冬水组inter-water wh 1.005 1.133 1.128 1.130 1061 0.982-1.0411.090-1.2261.088-1.2131.086-1.2210.994-1.207 小麦（总】 1.009 1.130 1.126 1.126 1.047 ed(toal)】 0.9821.0411.068-1.2261.066-1.2131.0651.2210.963-1.242 水稻（总 1.007 1.095 1.096 1.084 1.068 Rice(total) 0.974-1.0431.009-1.2941.008-1.2981.009-1.2870.974-1.414 玉米（总） 1.003 1.286 1.284 1.285 1.059 Maize(total 0.992=1.0241.097=1.6191.093=1.6191.097-1.6180.992-1.29% 四种作物（总 1.004 1.170 1.167 1.166 1.045 Four kinds of crope(totd 0.962=1.0431.009-1.6181.008=1.6191.009-1.6180.963-1.414 从表2可以看出，BLUE估值的GF在所有区试中都接近1，总平均为1.004。这是因为 BUE即算术平均值，二者的精度是等同的。当然，BLUE的各轮GF并不正好等于1，而是在 0.962~1.043间波动，这是由于交叉验证的数据分样只是所有可能分样的一部分，存在着一定的随机分样误差。一般来说，分样次数越大，误差越小。这里，分样误差造成的最大波动只有(1.043-1)=4.3%，对结果影响不大，所以本文3000次分样是足够的。如果误差过大（比如大于109万，方增加分样次数

!"#$ 和 %&。!"#$ 反映了估计值和验证观测值之间的接近程度；%& 则意味着某估值的精度相当于算术平均值精度的倍数。所以，!"#$ 越小，%& 越大，表明估值精度越高。上述过程中，采用 ’( 算法获得 )!!* 模型的奇异值和特征向量［+］。具体计算在微机上利用 ,-+. / 编程实现。 ! 结果与分析针对表 0 中共 1/ 套一年多点的平衡数据，按照上述方法对 -234、-23#56、-23#5、 -23#6 和 )!!* 估值分别进行 1/ 轮交叉验证，并统计各种作物和区试组别的精度增益倍数（%&）的均值和变幅，列于表 7。水稻和玉米由于数据较少，所以未分组别进行统计。另外， )!!* 模型随 8 取值的不同，可以得到多种 )!!* 估值，表中 )!!* 是指各轮验证中 %& 最大的一个，它代表 )!!* 系列模型在配合数据时所达到的最高精度。表 ! "# 次区试中的 $%&’、$%&( 和 )**+ 估值的交叉验证结果 ,-./0 ! 12344 5-/67-8639 204:/84 3; $%&’，$%&( -97 )**+ 69 "# 826-/4 作物 9:;8?@ 5:;A8<>;B 5?>B D?EF;:（BCH?F;:B 9L?B5M>?B5 (>N6: :65>;B /.OIJ P 0./0I 0.0/7 P 0.J7J 0.0/0 P 0.J/K 0.0/7 P 0.J7/ /.OIO P 0.7KQ 黄河流域春棉 "8:>B5 E;FF;B 0.//Q 0.770 0.701 0.77/ 0./7+ >B R6@@;S (>N6: :65>;B /.OK7 P 0./QQ 0./7J P 0.J/7 0./77 P 0.QOJ 0./7J P 0.J// /.OK7 P 0./I0 黄河流域夏棉 "AHH6: E;FF;B 0.//7 0.0/+ 0.0/7 0.0/+ 0./7I >B R6@@;S (>N6: :65>;B /.O17 P 0./Q0 0./QK P 0.011 0./QJ P 0.01J 0./Q1 P 0.011 /.OI+ P 0./OI 棉花（总） 0.//7 0.0II 0.0IJ 0.0II 0./QJ 9;FF;（B F;F?@） /.O17 P 0./QQ 0./7J P 0.J7J 0./77 P 0.J/K 0./7J P 0.J7/ /.OK7 P 0.7KQ 小麦黄淮春水组 "8:>B5TS?F6: SL6?F 0./0Q 0.07K 0.07Q 0.070 0./QJ UL6?F >B VA?B5LA?> :65>;B /.OOK P 0./Q1 0./1I P 0.0I7 0./11 P 0.0KO 0./1+ P 0.0I0 /.O1Q P 0.7J7 黄淮冬水组 U>BF6:TS?F6: SL6?F 0.//+ 0.0QQ 0.07I 0.0Q/ 0./10 >B VA?B5LA?> :65>;B /.OI7 P 0./J0 0./O/ P 0.771 0./II P 0.70Q 0./I1 P 0.770 /.OOJ P 0.7/K 小麦（总） 0.//O 0.0Q/ 0.071 0.071 0./JK UL6?F（F;F?@） /.OI7 P 0./J0 0./1I P 0.771 0./11 P 0.70Q 0./1+ P 0.770 /.O1Q P 0.7J7 水稻（总） 0.//K 0./O+ 0./O1 0./IJ 0./1I (>E（6 F;F?@） /.OKJ P 0./JQ 0.//O P 0.7OJ 0.//I P 0.7OI 0.//O P 0.7IK /.OKJ P 0.J0J 玉米（总） 0.//Q 0.7I1 0.7IJ 0.7I+ 0./+O !?>W（6 F;F?@） /.OO7 P 0./7J 0./OK P 0.10O 0./OQ P 0.10O 0./OK P 0.10I /.OO7 P 0.7OI 四种作物（总） 0.//J 0.0K/ 0.01K 0.011 0./J+ &;A: G>BC< ;D E:;8（< F;F?@） /.O17 P 0./JQ 0.//O P 0.10I 0.//I P 0.10O 0.//O P 0.10I /.O1Q P 0.J0J 从表 7 可以看出，-234 估值的 %& 在所有区试中都接近 0，总平均为 0. //J。这是因为 -234 即算术平均值，二者的精度是等同的。当然，-234 的各轮 %& 并不正好等于 0，而是在 /.O17 P 0./JQ 间波动，这是由于交叉验证的数据分样只是所有可能分样的一部分，存在着一定的随机分样误差。一般来说，分样次数越大，误差越小。这里，分样误差造成的最大波动只有（0./JQT0）X J.QY，对结果影响不大，所以本文 Q/// 次分样是足够的。如果误差过大（比如大于 0/Y），则需增加分样次数。 JQ7 作物学报 7K 卷万方数据

4期张群远等：品种区域试验中算术平均值、LUP和AMM估值的精度比较 433 表2中3种BUP估值的GF相差不大，均平均为1.170左右。这说明各种BLP的精度均高于算术平均值（为算术平均值的1.17倍左右），而且不同模型对其精度影响不大。相对而言，品种和试点效应都随机的BLUPge的精度稍高一点。不过，BLUP的精度在不同作物间有一定差别，BLUP的GF在棉花、小麦、水稻和玉米区试中的平均分别为1.188、1.130、1. 095和1.286，棉花和玉米中较高，水稻和小麦中稍低。另外，同一作物的不同区试组别间也有一定差别，如黄河春棉和夏棉区试的BLUPge的平均GF分别为1.221和1.105。但是，总的来看，所有区试中各种BLUP的GF都大于I,说明比起算术平均值来，BUP在各种区试中均有利于分析精度的提高。最后，表2中AMMI估值的平均GF为1.045，变幅为0.963~1.414，而且各种区试中都比较一致：说明虽然AM估值存在着比算术平均值精度高的情况，但普遍来说，精度提高不明显。 3讨论本文分析表明，BUP用于我国区试中品种×环境组合均值的估计，其精度可普遍提高到目前算术平均值的1.17倍左右。这意味着，在同样精度要求下，BLUP比算术平均值可以节约17%的试验小区重复数。这对我国区试精度和效率的提高来说很有意义。此外，若结合混合线性模型求解的一些方法，BUP还能很好地解决不平衡数据的问题6，刀。目前，BP 的方法在作物遗传育种中正得到越来越多的关注和应用8-B)。就本文分析结果来看，BP 的方法值得在我国试中加以研究和应用另外，虽然国外多数研究均表明，AMMI精度高于算术平均值(GF最大的达 4.30)24-18],但本文AMI精度的提高并不明显，这可能与我国区试数据的自身特点有关，譬如试点的范围和数目，品种的数目与类型，GE互作的强弱以及误差的大小等。这也说明一种统计模型或方法的精度高低，与它所面对的数据有关。当然，本文只是从品种×环境组合均值估计的角度探讨AMMI在我国区试中的精度特点；至于AMM其它方面（如品种稳定性分析)在我国区试中的应用效果及精度情况，尚需进一步研究。参考文献 1 Peipho HP.TAG,194,89:647-654 】莫感蛛发议验院计第二版上海上海科学载未饭让的论及应用合目天松世板中记 10g 8Zm小B S Weir..TAG,1994,89:160-166 876 391277 `0 16 Crossa J.HC Gauch.R W Zobel.Crop Sci..1990.30:493-500 nit,H Ketata et al 数据Cms.TAG,1998.96:80

表 ! 中 " 种 #$%& 估值的 ’( 相差不大，均平均为 )* )+, 左右。这说明各种 #$%& 的精度均高于算术平均值（为算术平均值的 )*)+ 倍左右），而且不同模型对其精度影响不大。相对而言，品种和试点效应都随机的 #$%&-. 的精度稍高一点。不过，#$%& 的精度在不同作物间有一定差别，#$%&-. 的 ’( 在棉花、小麦、水稻和玉米区试中的平均分别为 )* )//、)*)",、)* ,01 和 )*!/2，棉花和玉米中较高，水稻和小麦中稍低。另外，同一作物的不同区试组别间也有一定差别，如黄河春棉和夏棉区试的 #$%&-. 的平均 ’( 分别为 )*!!) 和 )*),1。但是，总的来看，所有区试中各种 #$%& 的 ’( 都大于 )，说明比起算术平均值来，#$%& 在各种区试中均有利于分析精度的提高。最后，表 ! 中 3445 估值的平均 ’( 为 )*,61，变幅为 ,* 02" 7 )* 6)6，而且各种区试中都比较一致；说明虽然 3445 估值存在着比算术平均值精度高的情况，但普遍来说，精度提高不明显。 ! 讨论本文分析表明，#$%& 用于我国区试中品种 8 环境组合均值的估计，其精度可普遍提高到目前算术平均值的 )* )+ 倍左右。这意味着，在同样精度要求下，#$%& 比算术平均值可以节约 )+9的试验小区重复数。这对我国区试精度和效率的提高来说很有意义。此外，若结合混合线性模型求解的一些方法，#$%& 还能很好地解决不平衡数据的问题［2，+］。目前，#$%& 的方法在作物遗传育种中正得到越来越多的关注和应用［/ 7 )"］。就本文分析结果来看，#$%& 的方法值得在我国区试中加以研究和应用。另外，虽然国外多数研究均表明，3445 精度高于算术平均值（’( 最大的达 6*",）［!，)6 7 )/］，但本文 3445 精度的提高并不明显，这可能与我国区试数据的自身特点有关，譬如试点的范围和数目，品种的数目与类型，’: 互作的强弱以及误差的大小等。这也说明，一种统计模型或方法的精度高低，与它所面对的数据有关。当然，本文只是从品种 8 环境组合均值估计的角度探讨 3445 在我国区试中的精度特点；至于 3445 其它方面（如品种稳定性分析）在我国区试中的应用效果及精度情况，尚需进一步研究。参考文献 ) &.; ? &* !"#，)006，/0：26+ 7 216 ! ’@AB= ? ’* $%&%’(%’)&* "+&*,(’( >C -./’0+&* 1’.*2 !3’&*( 4 :DE.F;.G，H.I J>GK* )00! " ?.LM.GE>L N O* 5’06.%3’)(，)0+1，")：6!" 7 66+ 6 莫惠栋* 农业试验统计（第二版）* 上海：上海科学技术出版社，)00! 1 &G.EE P ?，# & (D@LL.GQ，.R @D* 786.3’)&* -.)’9.( 4 N@STG;M-. %L;F &G.EE，$>LM>L* )0/2 2 王松桂* 线性模型的理论及应用* 合肥：安徽教育出版社，)0/+ + 朱军* 遗传模型分析方法* 北京：中国农业出版社，)00+ / U=A V，# W P.;G* !"#，)006，/0：)2, 7 )22 0 &@LR.G X 4，( $ 3DD.L* :309 $)’，)001，"1："0+ 7 6,1 ), #.GL@GM> O* :309 $)’，)002，"2：/+! 7 /+2 )) #.GL@GM> O* !"#，)00+，01：211 7 210 )! #.GL@GM> O* !"#，)00/，0+：6+" 7 6+/ )" #.GL@GM> O* :309 $)’，)000，"0：)!++ 7 )!/! )6 ’@AB= ? ’，O P U>T.D* !"#，)0//，+2：) 7 ), )1 ’@AB= ? ’* 5’06.%3’)(，)0//，66：+,) 7 +,1 )2 NG>EE@ V，? ’ ’@AB=，O P U>T.D* :309 $)’ 4，)00,，",：60" 7 1,, )+ H@B=;R 44，’ H@B=;R，? Y.R@R@，.R @D* !"#，)00!，/"：10+ 7 2,) )/ 4>G.L>Z’>L[@D.[ V，V NG>EE@* !"#，)00/，02：/," 7 /)) 6 期张群远等：品种区域试验中算术平均值、#$%& 和 3445 估值的精度比较 6"" 万方数据

品种区域试验中算术平均值、 BLUP和AMMI估值的精度比较作者：张群远，孔繁玲，杨付新作者单位：张群远,孔繁玲(中国农业大学植物遗传育种系)，杨付新(中国农业科学院棉花研究所) 刊名：作物学报英文刊名： ACTA AGRONOMICA SINICA 年，卷(期)： 2001，27(4) 引用次数： 4次参考文献(18条) 1.Peipho H P 查看详情 1994 2.GauchHG Statistical Analysis of Regional Yield Trials 1992 3.Henderson C R 查看详情 1975 4.莫惠栋农业试验统计 1992 5.Press w H.B P Flannery Numerical Recipes 1986 6.王松桂线性模型的理论及应用 1987 7.朱军遗传模型分析方法 1997 8.Zhu J.B S Weir 查看详情 1994 9.Panter D M.F L Allen 查看详情 1995 10.Bernardo R 查看详情 1996 11.Bernardo R 查看详情 1997 12.Bernardo R 查看详情 1998 13.Bernardo R 查看详情 1999 14.GauchHG.R W Zobel 查看详情 1988 15.GauchHG 查看详情 1988 16.Crossa J.H G Gauch.R W Zobel 查看详情 1990 17.Nachit MM.G Nachit.H Ketata 查看详情 1992 18.Moreno-Gonzalez J.J Crossa 查看详情 1998 相似文献(1条) 1.期刊论文张群远.孔繁玲.杨付新作物品种区域试验中品种均值估计的模型和方法--算术平均值、加权最小二乘估值和BLUP的比较 -作物学报2003,29(6) 针对作物区域试验中的品种均值估计问题,根据混合线性模型的一般原理,总结和提出多种加权最小二乘估计 (WLSE)和最佳线性无偏预测(BLUP)的方法,推导了这些方法的平衡数据计算简式;同时,利用14套2年多点的棉花区试资料和一套4年多点的棉花品种试验对这些方法的预测效果进行验证比较.结果表明,与算术平均值相比,以环境内误差方差倒数加权的WLSE估值的预测精度(包括预测差的大小和品种排名的一致性)明显不同,但其高低因数据而异;其他WLSE估值以及BLUP的预测结果差别不大,和算术平均值以及相互间的相关系数和秩相关系数均在0.93以上. 引证文献(4条)