第八章卡方检验 第一节 2×2表x2检验 第二节 行X列表x2检验 第三节 配对资料x2检验 3
3 第一节 2×2表x 2检验 第二节 行×列表x 2检验 第三节 配对资料x 2检验

应用条件 常用于两个或多个样本率或构成比之 间的比较的显著性检验。 基本思想 检验实际频数和理论频数的差别是否 由抽样误差所引起的,即由样本率 (或样本构成比)推断总体率(或总 体构成比)。 4
4 应用条件 常用于两个或多个样本率或构成比之 间的比较的显著性检验。 基本思想 检验实际频数和理论频数的差别是否 由抽样误差所引起的,即由样本率 (或样本构成比)推断总体率(或总 体构成比)

基本公式 (ARC -TRC) x2= TRC TRC nRNC L v=(行数-1)(列数-1) 5
5 基本公式 ( ) n n n T T A T x R C RC RC RC RC = − = 2 2 υ=(行数-1)(列数-1)

第一节2X2表x2检验 (一)使用X2检验的 基本公式 四格表X2检验 (二)四格表资料X2 检验的专用公式 二、四格表资料X检 验 的连续性校正 (一)两组样本例数 不等时的确切概率法 三、四格表资料X检 验 (二)两组样本例数 的确切概率检验法 相等时的确切概率法 6
6 第一节 2×2表x 2检验 一、四格表X 2检验 二、四格表资料X 2检 验 的连续性校正 (一)使用X 2检验的 基本公式 (二)四格表资料X 2 检验的专用公式 三、四格表资料X 2检 验 的确切概率检验法 (一)两组样本例数 不等时的确切概率法 (二)两组样本例数 相等时的确切概率法

(一)使用X2检验的 基本公式 Bi B2 合计 A a b a +b A2 c d c +d n-a+b+ 合计 a+c b+d c+d 7
7 (一)使用X 2检验的 基本公式 B1 B2 合计 A1 a b a +b A2 c d c +d 合计 a+c b+d n=a+b+ c+d
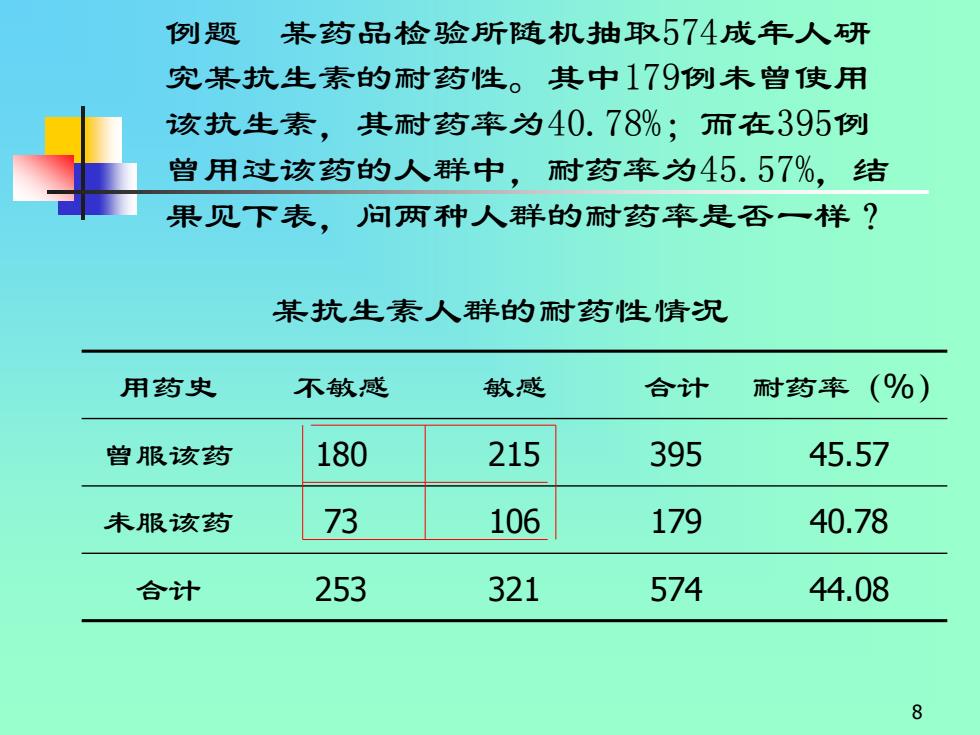
例题 某药品检验所随机抽取574成年人趼 究某抗生素的耐药性。其中179例未曾使用 该抗生素,其耐药率为40.78%;而在395例 曾用过该药的人群中,耐药率为45.57%,结 果见下表,问两种人群的耐药率是否一样? 某抗生素人群的耐药性情况 用药史 不敏感 敏感 合计 耐药率 (%) 曾服该药 180 215 395 45.57 未服该药 73 106 179 40.78 合计 253 321 574 44.08 8
8 例题 某药品检验所随机抽取574成年人研 究某抗生素的耐药性。其中179例未曾使用 该抗生素,其耐药率为40.78%;而在395例 曾用过该药的人群中,耐药率为45.57%,结 果见下表,问两种人群的耐药率是否一样? 用药史 不敏感 敏感 合计 耐药率(%) 曾服该药 180 215 395 45.57 未服该药 73 106 179 40.78 合计 253 321 574 44.08 某抗生素人群的耐药性情况

1、建立检验假设,确定检验水准 Ho: 两种人群对该抗生素的耐药率相同兀1二兀2 H:两种人群对该抗生素的耐药率不同元1卡元2 =0.05 2、计算统计量 TRC nRNC n 395×321 T =220.90 574 180 215 395 395×253 T12= =174.10 73 106 179 574 179×253 253 321 574 T22 =78.90 574 179×321 T21 =100.10 574 9
9 1、建立检验假设,确定检验水准 H0:两种人群对该抗生素的耐药率相同π1 = π2 H1:两种人群对该抗生素的耐药率不同π1 ≠ π2 α= 0.05 2、计算统计量 100.10 574 179 321 78.90 574 179 253 174.10 574 395 253 220.90 574 395 321 2 1 2 2 1 2 1 1 = = = = = = = = T T T T n n n T R C RC = 180 215 395 73 106 179 253 321 574

(ARc-TRC)2 2=∑ TRC 2= (180-174.10)2 (215-220.90)2 174.10 220.90 (73-78.90)21(106-100.10)2 78.90 100.10 =0.20+0.16+0.44+0.35=1.15 3、确定P值和判断结果 v=(2-1)(2-1)=1查x2界值表 X20.051)=3.84>x2=1.15,得P>0.05 按=0.05水准接受H),拒绝H1可认为两种人 群对该抗生素耐药性的差异无统计学意义。 10
10 ( ) 0.20 0.16 0.44 0.35 1.15 100.10 (106 100.10) 78.90 (73 78.90) 220.90 (215 220.90) 174.10 (180 174.10) 2 2 2 2 2 2 2 = + + + = − + − + − + − = − = x T A T x RC RC RC 3、确定P值和判断结果 ν=(2-1)(2-1)=1 查x 2界值表 X 2 0.05(1)= 3.84 > x2 =1.15,得P>0.05 按α=0.05水准接受H0,拒绝H1可认为两种人 群对该抗生素耐药性的差异无统计学意义
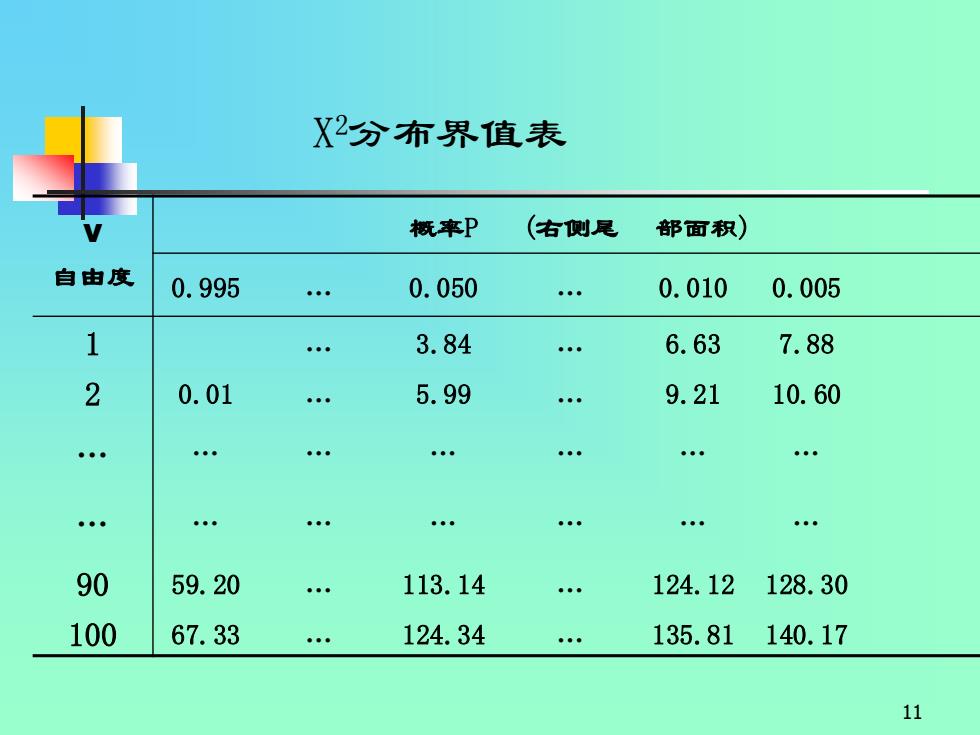
X2分布界值表 概率P (右侧尾 部面积) 自由度 0.995 0.050 0.010 0.005 1 3.84 6.63 7.88 2 0.01 5.99 9.21 10.60 90 59.20 113.14 124.12128.30 100 67.33 124.34 135.81140.17 11
11 ν 概率P (右侧尾 部面积) 自由度 0.995 … 0.050 … 0.010 0.005 1 … 3.84 … 6.63 7.88 2 0.01 … 5.99 … 9.21 10.60 … … … … … … … … … … … … … … 90 59.20 … 113.14 … 124.12 128.30 100 67.33 … 124.34 … 135.81 140.17 X 2分布界值表

(二)一四格表资料X检验的专用公式 ad-bep'n (a+b)c+d)a+cXb+d) 180 215 395 73 106 179 253 321 574 x2= (180×106-215×73)2×574 (395)179)253)321) =1.15 12
12 (二)四格表资料X 2检验的专用公式 ( ) (a b)(c d )(a c)(b d ) ad bc n x + + + + − = 2 2 ( ) ( )( )( )( ) 1.15 395 179 253 321 180 106 215 73 574 2 2 = − x = 180 215 395 73 106 179 253 321 574