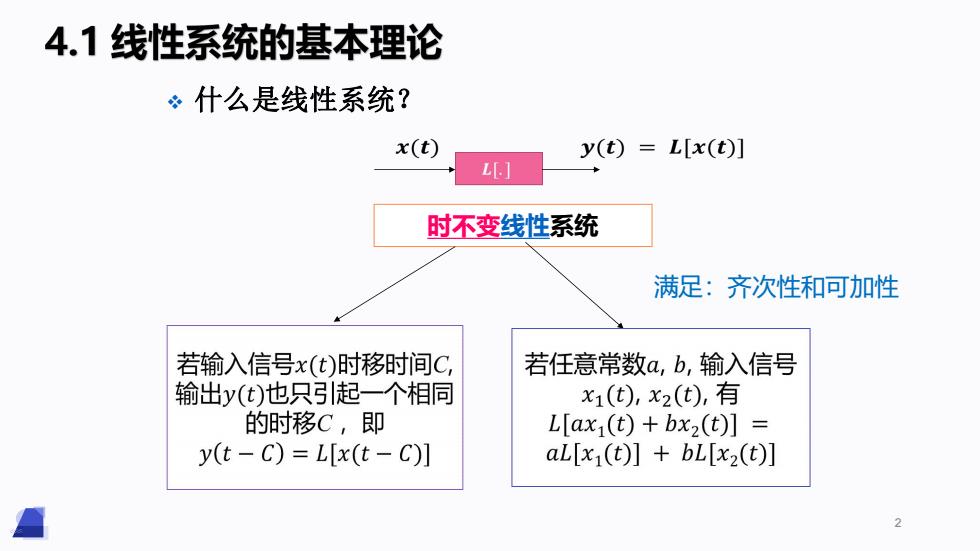
4.1线性系统的基本理论 ÷什么是线性系统? x(t) y(t)=L[x(t)] L[] 时不变线性系统 满足:齐次性和可加性 若输入信号x(t)时移时间C, 若任意常数a,b,输入信号 输出y(t)也只引起一个相同 x1(t),x2(t),有 的时移C,即 L[ax(t)+bx2(t)] y(t-C)=L[x(t-C)] aL[x(t)]bL[x2(t)] 2
2 时不变线性系统 v 什么是线性系统? 满足:齐次性和可加性
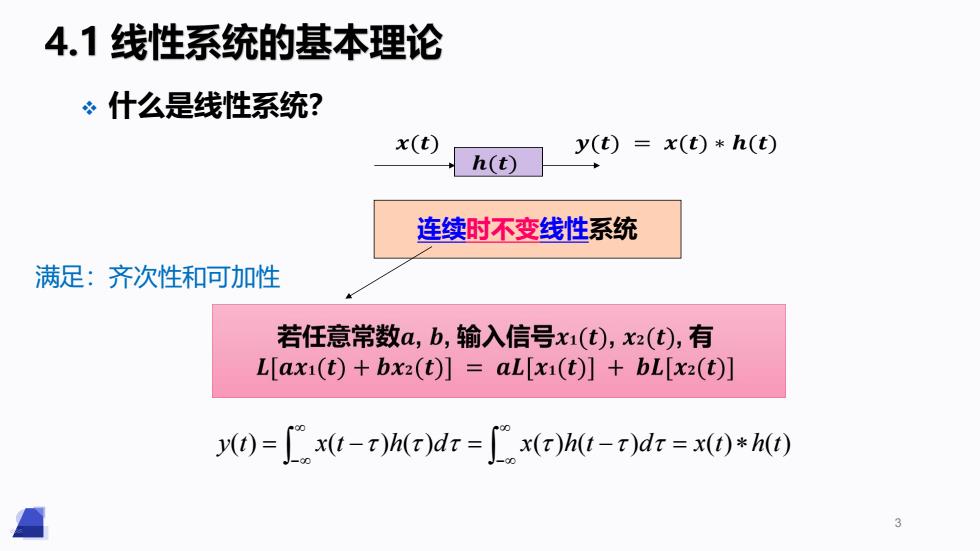
4.1线性系统的基本理论 什么是线性系统? x(t) y(t)=x(t)*h(t) h(t) 连续时不变线性系统 满足:齐次性和可加性 若任意常数a,b,输入信号x1(t),x2(t),有 L[axi(t)+bx2(t)]=aL[xi(t)]+bL[x2(t)] ()=[x(-t)h()dr=x(h(t-)dr=x(t)*h(t)
3 连续时不变线性系统 v 什么是线性系统? y(t) x(t )h( )d x( )h(t )d x(t)h(t) 满足:齐次性和可加性

系统的几个特性: ■系统的无记忆性:如果一个系统的输出仅仅取决于该时刻(即当前时刻)的输入,那么就 称这个系统具有无记忆性。 ■可逆性:如果一个系统在不同输入下,导致不同输出,那么该系统就是可逆的,在强调一 遍是不同输入(输入一定要不同)导致不同输出。 ■因果性:如果一个系统的输出只取决于该时刻(即当前时刻)及过去时刻的输入,那么就 称这个系统具有因果性。 ■稳定性:如果一个系统的输入是有界的(即输入的幅度不是无界增长的),并且输出也有 界,则该系统具有稳定性。 ■时不变性:若系统的特性和行为不随时间而变,该系统就是时不变的。 ·线性:若系统同时满足比例性(齐次性)和可加性或总称为叠加性则称系统具有线性
n 系统的无记忆性:如果一个系统的输出仅仅取决于该时刻(即当前时刻)的输入,那么就 称这个系统具有无记忆性。 n 可逆性:如果一个系统在不同输入下,导致不同输出,那么该系统就是可逆的,在强调一 遍是不同输入(输入一定要不同)导致不同输出。 n 因果性:如果一个系统的输出只取决于该时刻(即当前时刻)及过去时刻的输入,那么就 称这个系统具有因果性。 n 稳定性:如果一个系统的输入是有界的(即输入的幅度不是无界增长的),并且输出也有 界,则该系统具有稳定性。 n 时不变性:若系统的特性和行为不随时间而变,该系统就是时不变的。 n 线性:若系统同时满足比例性(齐次性)和可加性或总称为叠加性则称系统具有线性。 系统的几个特性:

4.2随机信号通过连续时间系统的分析 4.2.1时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距 ~输入为随机信号X(t)的某个实验结果的一个样本函数x(t),则输出为: ()=[h()x(t-t)d 一个确定性函数 系统的单位冲激响应 一个确定性函数 5
5 4.2.1 时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距 0 y(t) h( )x(t )d 系统的单位冲激响应 一个确定性函数 一个确定性函数

4.2随机信号通过连续时间系统的分析 4.2.1时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距 对于随机信号x(),任意一个样本函数均成立。 那么对于所有的试验结果,系统输出为一族样本函数,这族样本函数构 成随机过程 Y(t)=[h(r)X(t-z)dr=h(t)*X(t) 6
6 0 Y(t) h( )X (t )d h(t) X (t) : 那么对于所有的试验结果,系统输出为一族样本函数,这族样本函数构 成随机过程 4.2.1 时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距

4.2随机信号通过连续时间系统的分析 4.2.1时域分析法 定理1:设Y(t)=L[X(t)],则E{Y(t)}=L{E[X(t)]} 即算子L、E可以交换次序。 证明:y:(t)=L(x(t) Y'(t)=是by,(e)+y2()++y.(t]=1[21L(x:()】=L∑1x:()=[X'(t)】 两边均对n取极限无穷大,则有 E[Y(t)]=L(E[X(t)])
4.2.1 时域分析法

4.2随机信号通过连续时间系统的分析 4.2.1时域分析法 1、输出表达式 (零状态响应,因果系统】 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距 证明 my (t)=E[Y(t)]=El h(r)X(t-t)dr] =∫。h(r)E[X(t-r]dr =∫nh(r)mxu-t)dr 若X(t)为平稳随机过程,则 =mx(t)*h(t) my=mx h()d
8 Y 0 m (t) E[Y(t)] E[ h( )X (t )d ] 0 h( )E[X (t )]d X 0 h( )m (t )d X m (t) * h(t) 证明 Y X 0 m m h( )d 4.2.1 时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距

4.2随机信号通过连续时间系统的分析 4.2.1时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距 结论:由于系统的输出是系统输入的作用结果,因此,系统输入输出之间是 相关的,系统输入输出相关函数为 Rxy(41,t2)=Rx(41,t2)⑧h(t2) Ryx(1,t2)=Rx(t,t2)h() 9
9 XY 1 2 X 1 2 2 R (t ,t ) R (t ,t ) h(t ) YX 1 2 X 1 2 1 R (t ,t ) R (t ,t ) h(t ) 结论:由于系统的输出是系统输入的作用结果,因此,系统输入输出之间是 相关的,系统输入输出相关函数为 4.2.1 时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距

4.2随机信号通过连续时间系统的分析 证明: 因为 X(t)Y(t)=X(t)L[X(t)]=L[X(t)x(t)] E[X(t)Y(t]=E(L[X(t)x(t=L{E[X(t)X(t 令t=t2.可得 Rxy(t1t2)=Lt([Rx(t,t2)]) 同理可证 Ryx(t1t2)=Lt([Rx(tit2)]) 因此 Ry(tt)=L Lt([Rx(tt2D) 10
10

4.2随机信号通过连续时间系统的分析 4.2.1时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距 结论:已知系统输入随机信号的自相关函数,可以求出系统输出端的自相 关函数 R(t,t2)=EIY(G)Y(t2】=h(t)⑧h(t2)⑧Rx(t,t2) 11
11 结论:已知系统输入随机信号的自相关函数,可以求出系统输出端的自相 关函数 Y 1 2 1 2 R (t ,t ) E[Y(t )Y(t )] 1 2 X 1 2 h(t ) h(t ) R (t ,t ) 4.2.1 时域分析法 1、输出表达式(零状态响应,因果系统) 2、输出的均值 3、系统输入与输出之间的互相关函数 4、系统输出的自相关函数 5、系统输出的高阶距