
生物数学学报 I.Biomath。 9(4)(1994),185-188 非线性模型参数估计的一种新方法 章元明 (四川牧普区华,四川昌,632460) A NEW METHOD FOR ESTIMATING PARAMETERS IN NONLINEAR MODEL Zhang Yuanming ABSTRACT According to orthogonal experiment and sequential estimation,a new method estimating parameters in nonlinear model was suggested in this paper,and it was the same results as Gauss-Newton method. Key words:Nonlinear model,Parameter estimation,Orthogonal experiment 【提要】本文以正交试验为工具,利用序贯思想,提出了非线性模型参数估计的 正交试验法。该法简单易行,便于推广,且与Gauss一Newton法的结果相当。 关健词:非线性模型,参数估计,正交试险。 在应用中,人们常把非线性模型线性化以估计参数,但是,它仅是线性化模型最小二 乘(LS)估计,不是非线性模型的LS估计。当然,非线性模型的LS估计方法是有的,如Gau ss-Newton(筒称G-N法)及其改良法、Marquardi法及序贯法c)等.不过,这些方法对 应用者来说可能有一定难度,导致它们未被广泛使用。因而,寻找一种应用者容易理解的 方法是有应用价值的。为此,本文便以正交试验为工具,利用序贯思想提出一种新方法。 一、基本原理 1、非线性棋型 (1)两参数模型 (1 y=ab* (2=ax (3 y=aet (4 y=acbx (5g=ac3: (6g=1/八a+bx)(7y=x八a+bx)(8y=(a+bx)/x 1994年3月12日收到. 14-00China Academic Joumal Electronic Publishing House All rights reserved.hp://ww.cnki.et
生 物数学学 报 。 优 认 , 一 非线性模型 参数估计的一种新方法 章 元 明 四 川 畜牧 兽 医 学 院 , 四 川荣 昌 , 比 人皿 飞 。己 几 亡 盔 租 生 位 , , , 一 匡 , , 十 【 提 要 】勇本文 以正 交 试验 为工具 , 利 用 序 贯 思 想 , 提 出了 非 线性模 型 参数估计 的 正 交试验法 。 该法简单 易行 , 便于 推广 , 且与 翻 一 。、 法的结果相 当 。 关 键 饲 非线性模型 , 参数估计 , 正交试验 。 一 在应 用 中 , 人们常把非线性 模型 线性化 以估计参数 , 但是 , 它 仅是线性 化模型 最小 二 乘 估计 , 不是非线性模 型 的 估计 。 当然 , 非线性模型 的 估计方法是有的 , 如 一 简称 一 法 及其改 良法 、 法及序 贯法 〔‘ 〕等 。 不过 , 这些方法对 应用 者来 说可 能有一定难度 , 导致它们 未被广 泛使用 因而 , 寻找一种应 用 者容 易理 解 的 方法是有应 用价 值的 。 为此 , 本文便 以 正交试验为工具 , 利用 序 贯 思 想提 出一 种新方法 。 一 、 基 本原 理 、 非 线 性模 型 一 两参数模型 万二 万 。 夕 , ‘ 梦 石 夕二 二 兮 八 夕 飞了叮矛、 ‘八 万二 己 ‘叮、矛 勺上目了 年 月 日收 到

186 章元明 9卷 (2)三参数校型(1 Logistic模型=k/儿1+cx(a-bx)门 (2 Gompertz模型y=kcxp[-bcx(-ax)] 当然,本文提出的方法不只是适合以上儿个模型,对一般非线性模型(日,x)一般 也是可行的。其参数估计方法一般是使工1(g-)”(或工1y.~)为最 小,这称为参数估计的最小二乘法或最小一乘法. 2。参数估计方法(1)确定参数初值0:)及因素(参数)水平间距△),并令 8b=0:0y,△)=△0). 通过线性化方法或经验得到参数的估计值作为参数初值(),对两参数模型,很容 易获得0);对三参数模型,如知Logistic模型和Gomper!z模型,取一个比所有观察值大 的数作为k,由此就转化为两参数模型的情形。 △()可通过线性化模型参数的1倍标准差转换后米确定。 (2)正交试验的安排及实施,待估参数个数为正交试验的因素数,各因素的 水平数均为3,由此,因素各水平为61)-△D,81,日)+△i),选择合适的正交 表,如L。(3),正交表前儿列安排各因素进行正交试验。 (3)正交试验的结果分析以剩余平方和为试验指标,通过直税分析得出最佳因 素水平组合,并算出其剩余平方和,比较这10个剩余平方和(若进行了一次正交试验, 则加上前一次正交试验的最小剩余平方和,即比较11个剩余平方和),其最小剩余平方 和所对应的一组参数值为本次正交试验的最优参数估计值0)*. (4)若满足闵值条件△)<(给定的一小正激),B)*为该轮试验的参数估计值, 否则,令△*)=△)/2,0)=0)*,转入(2). 对两参数模型,通过以上的方法一般可得到较好的参数估计值,几乎与G一N法一致, 对三个参数模型等,一般地,上述步骤得不到较好的估计值,往往需要在前面结果的基 础上重新确定因素水平间距△),多次重复这一过程会得到令人满意的参数估计值. 二、实例分析 例2·1引用文献[5](P517528)重伤病人资料配合非线性模型影=acx(bx), 其结果见表1.从表1可知,新方法与Gass一Newton法结果(引自文[5】P。:,)儿乎 表1 重伤病人资料参数估计值与拟合精度 方 Gauss-Newton 58.6065 -.03959 49.4593.987507 新方热 58.60504 -,03958693 49.45926.987507 4-009 China Academie oumal Publishing House.All rights reserved.hup://www.cnki.net
章 元 明 卷 三参数模型 ‘ 模型 二 〔 十 。砂 一 〕 二 。 模型 夕二 仁一 石。 一 〕 当然 , 本文提 出的方 法不 只是适合 以上几个模型 , 对一般非线性模型 了 , 一 般 也是 可行 的 其参数估计方 法一般是使 二 、 、 , , 一 认 “ 或 习 岁 , , 一 欲 为最 曰 ’ ‘ 目 一 ’目 护 ’ ‘曰 沐 一 二 、 沙 , ‘ 产 、 自 ‘ , ” ‘ ’了 小 , 这 称为 参数 估计 的最小二 乘法或最小一 乘法 。 。 参数 估 计 方 法 确定参数初值 “ 及 因素 参数 水 平 间距 △ ‘ “ 、 , 并令 ‘ ” ’ , △ △ 。 通 过 线性 化方法或 经验得到参数的估计值作为参数初值 “ 。 对两参数模型 , 很容 易获得 “ 对三参数模型 , 如 ’ ’模型 和 。对 模型 , 取一 个 比所有 观察值 大 的数作为 , 由此 就转化为 两参数模型 的情形 △ ” 可 通过线性化模型参数的 倍标 准差转 换后来 确定 。 正 交试验 的安排及 实 施 待估 参 数个数为正 交试 验的因素个数 , 各因素 的 水平数均为 , 由此 , 因素 各水平为 戈 一 △ , 小 , “ 十 △“ , 选 择合适 的正 交 表 , 如 。 ‘ , 正 交表 前儿列 安排 各因素进行正 交试验 。 正 交试 验 的结果分析 以 剩余平方和 为试 验指标 , 通 过直观分析 得 出最佳 因 素水 平组 合 , 并算 出其剩余平方 和 , 比较这 个 剩佘平方 和 若进行 了一 次正 交 试 验 , 则加 上 前一 次正交 试验 的最小 乘余平方和 , 即 比较 个 剩余平方和 , 其最小 剩余平 方 和所对应 的一组 参数 值为本 次正 交试验 的最优 参数估计值 ‘ 气 若满足 阂值条件 △ 。 给定的一小正 数 , 为该轮试验 的参数估计值 否 则 , 令 △ ‘ ’ 二 △ , , 日‘ 十 ‘ ‘ 气 转入 。 对两参数模型 , 通过 以上 的方法一般 可得到较好 的参数估计值 , 几 乎 与 一 法一致 对 三 个参数摸型等 , 一般地 , 上 述步骤得不 到较好 的估计值 , 往往需要在前面结果 的基 础 上 重新确 定因素水平 间距 △弋 ” , 多 次重复这一 过程会得到令人满意 的参数估计值 二 、 实例 分 析 例 · 引用 文 献 〔 〕尸 重伤病人资料配合非 线性模型 , 。 乙 。 其结果见表 从表 可 知 , 新方法与 一 留 法结果 引 自文 〔 尸 。 , 几乎 表 贡伤 病人资 料 ‘ “ 飞 参数估 计 值 与拟 合精 度 方 法 , 一 。 一 。 。 新 方 法 。 一 。
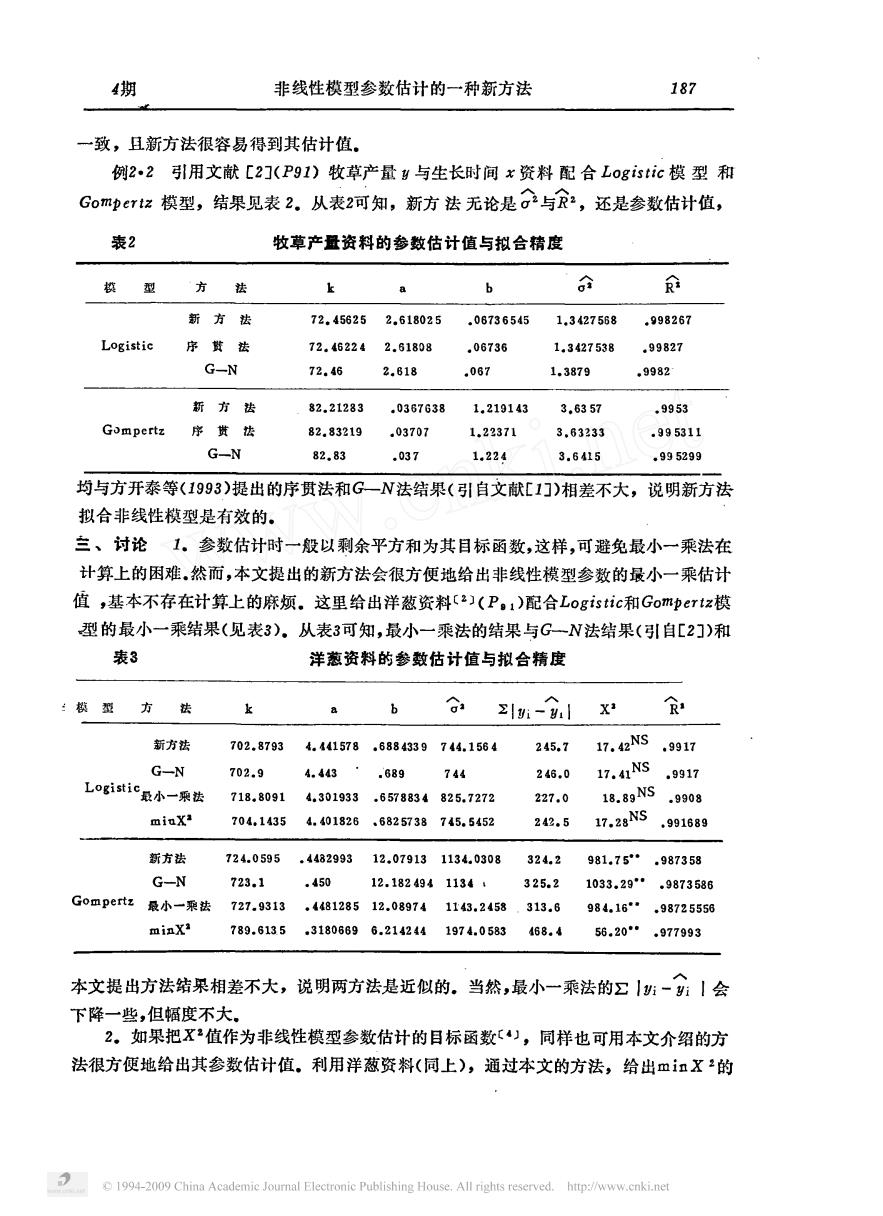
4期 非线性模型参数估计的一种新方法 187 一致,且新方法很容易得到其估计值。 例2,2引用文献[2](P91)牧草产量y与生长时间x资料配合Logistic模型和 G0mpTz模型,结果见表2.从表2可知,新方法无论是可2与2,还是参数估计值, 表2 牧草产量资料的参数估计值与拟合精度 换型方法 上 b 新方法 72.456252.618025.067365451.3427568 ,998267 序齿 72.462242.51808 .06736 1.3427538 .99827 G-N 72.46 2.618 .087 1.3879 .9982 方齿 82.21283 .0367G38 1.2101433,6357 ,9953 G的mpertz序货齿 82.83219,03707 1.22371 3,63233 .995311 G-N 82.83 .037 1.224 3.6415 ,995299 均与方开泰等(1993)提出的序贯法和G一N法结果(引自文献[1)相差不大,说明新方法 拟合非线性模型是有效的。 兰、讨论1,参数估计时一般以剩余平方和为其目标函数,这样,可避免最小一乘法在 计算上的困难,然而,本文提出的新方法会很方便地给出非线性模型参数的最小一乘估计 值,基本不存在计算上的麻烦.这里给出详葱资料2(P,:)配合Logistic和Gompertz模 型的最小一乘结果(见表3)。从表3可知,最小一乘法的结果与G一N法结果(引自[2])和 表3 洋葱资料的参数估计值与拟合精度 型方齿 b :-lX3 R 新方法 702.87934.41578.888439744.1564 245.717.62NS9917 G-N 702.94.443·,589744 26.017.4NS.917 Logisic0小-齿71.0914.301933657834825,722 227.0 18.89NS.9908 704.14354,4018266825738745.5452 242.517,2NS ,991689 断方费 724.0595.448299312.079131134,0308 324.2 981.75987358 G-N 723.1 .450 12.1824941134 325.2 1033,29 ,9873536 G0 mperts最小一果法727.9313.448128512.08074118.2458.313.6984.16.9872556 miaxi 789.513531806896.2142441974.0583468.456,20,977993 本文提出方法结采相差不大,说明两方法是近似的。当然,最小一乘法的Σ1班-:丨会 下降一些,但幅度不大 2。如果把x产值作为非线性模型参数估计的目标函数),同样也可用本文介绍的方 法很方便地给出其参数估计值。利用洋葱资料(同上),通过本文的方法,给出m知X:的
期 非 线性模型参数估计 的一种新方法 召 一致 , 且新方法很容易得到其估计值 。 例 引用文献 〔 〕尸 牧草产量 穿 与生长时 间 资料 配 合 ‘ 模 型 和 仰 。 模型 , 结果见表 从表 可 知 , 新方 法 无论是 争载 , 还是参数估计值 , 表 牧草产且资料 的参数估计 值 与拟合精度 模 型 方 法 介 奋 新 方 序 赏 一 一 。 。 。 。 。 。 法法 。 。 。 一 新 方 。 序 贯 。 。 。 。 。 。 。 。 。 。 。 法法 一 。 。 均与方开泰等 提 出 的序贯法和 一 法结果 引 自文献 〔 〕相 差不大 , 说 明新方法 拟 合非 线性模型是有效 的 。 兰 、 讨 论 。 参数估计时 一般 以 剩余平方和 为其 目标 函数 , 这样 , 可 避免最小一 乘法在 计算上的困难 然而 , 本文提 出的新方法会很方便地给 出非线性模型参数 的最小一 乘估计 值 , 基 本不存在计算上 的麻烦 。 这里 给 出洋 葱 资料 〔“ 〕 。 配合 ‘和 。 , 。 招模 型 的最小一乘结果 见 表 。 从表 可 知 , 最小一 乘法的结果 与 一 法结果 引 自〔 〕和 表 洋 葱资料的 参数估计值 与拟 合 精度 模 型 方 法 、 言 , 宝 。 。 。 。 通 。 。 。 甘 通 新方 法 一 最 小一乘 法 住 。 。 。 。 。 , 。 。 。 。 。 艺 夕 一 , 。 。 。 。 新方 法 一 乙 最小 一 乘 法 牡 。 。 。 。 。 。 一 一 一 。 一 。 一 。 。 。 。 。 通 。 。 。 二 。 二 。 二 。 二 一 本文提 出方法结果相差不大 , 说明两方法是近似的 当然 , 最小一 乘法的二 , 一 认 会 下 降一些 , 但幅度不大 。 。 如果把 名值作为非线性模型 参数估计的 目标 函数 〔通 , 同样也 可用 本文介绍的方 法很方便地给出其参数估计值 。 利用 洋葱资料 同上 , 通过本文 的方法 , 给出 忍 的

188 章元明 9卷 参数估计值(见表3)。从表3可知,无论用哪种方法,洋葱资料均与Logistic模型相配;然 而,对Gompertz模型,用minX方法时,即使X:值下降近20倍,它仍然与Gompertz模 型不配,由此推知,选择最优模型时运用最小一乘法或最小二乘法是适合的。另外,当 Gompertz模型与资料不配时,minX2的结果与其它方法差异较大,且0增加,下 降,由此说明,miX方法)是否是提高非线性模型拟合精度的有效方法还有待于进 一步探讨。 参考文献 〔1)方开泰等,本浅生回归慎型参数估计的一个新并法,应用数学学报(3),1993:366一377. 〔2)供再吉等译,Ratkowsk切,D.A,若,春线性回白筷型-一统一实用方法,南京大学出版社,1985. C3)英惠佛,农业试验统计,上海科学找术由版杜,1984, C杨运济等,提高非线性核型都合结果可靠性的一种方法一一-“'值Marquardt法”,生物:学学报(3),1993 150155. C5)张勇等承,Jbh1 Neter etc.奢,应用线性同归型,中国计出反,1990 C 1994-2009 China Academic Joural Electronic Publishing House.All rights reserved.http://www.cnki.ne
章 元 明 卷 参数估计值 见 表 。 从表 可 知 , 无 论用 哪 种方法 , 洋葱资料均与 模型相配 然 而 , 对 模型 , 用 “ 方法时 , · 即使 值下 降近 倍 , 它仍然 与 模 型不 配 由 此 推知 , 选 择最优模型时运用 最小一 乘法或最 小二 乘法是适合的 。 另外 , 当 召。 招 模 型 与资料不 配时 , “ 的结果 与其它 方 法 差 · 异较 大 , 且砂 增加 , “ 下 降 , 由此 说 明 , 么方法 ‘ 〕是否 是提 高非 线性模型 拟合精度 的有效方法还有 待 于进 一步 探讨 。 参 考 文 献 〔 〕方 开 泰 等 , 非 浅 性 回 归 摸 型 参 数 估 计 的 一 个 新 算 法 , 应 用 数 学学 报 , 。 〔 〕洪 再 吉 等 译 , , 。 。 著 , 非线 性 回 归模 型 一一统一 实 用方 法 , 南 京 大学 出 版 社 , 。 〔 〕莫 惠 拣 , 农 业 试 验 统 计 , 上 海 科 学 技术 出版杜 , ‘ 〔幻 杨 运 清 等 , 提 高 非 线 性模 型 拟 合 结果 可靠 性 的 一 种 方 法一一 “ 砂 值 法 ” , 生 物数 学学 报 , 〕张 勇 等 译 , 住 著 , 应 用 线 性回 归 模型 , 中国统 计 出版社 , 。