
第27卷第5期 作物学报 Vol.27,No.5 2001年9月 ACTA AGRONOMICA SINICA Sept.,2001 线性回归分析的逆预测' 莫惠栋 (扬州大学数量遗传研究室,江苏扬州225009) 提要逆预测又称逆回归,是从依靠变数Y的某一定值Y,预测独立变数X的对应值X。及其100(1 一)%可信区间。本文详细地解释了逆回归的原理、方法和注意问题,推导了逆回归的一些基本公式, 并用两个实例分别说明Y。为Y总体的条件平均数和单一观察值时的逆回归程序。 关键词线性回归:逆回归 Inverse Prediction in Linear Regression Analysis MO Hui-Dong (Lab of Quantitative Genctics.Yangshou Uniwersity.Yangshou 225009.China) Abstract The inverse prediction,i.e.,inverse regression,which is predicting an inde pendent variate Xo and its 100(1-a)%fiducial limits from a given value Yo of dependent variable Y.In the present paper,the principle and method for inverse regression were ex- plained and some fundamental formulae were derived and extended.Two real examples were taken to demonstrate the inverse regression procedure when Yo was a conditional mean and a single observed variate of Y population,respectively. Key words Inverse regression:Linear regressior 回归分析是处理具有自变数(X)和依变数(Y)之分的试验资料的统计方法,通常要求X 固定,Y随机。所以分析的基本目的是由X估计或预测Y,其k元线性回归模型的一般形式 为Y,=a十b,X+e(i=1,2,,k;j=1,2,…,n)们。但是,在有些情况下,研究者需要 了解的却是Y在某一Y。时的X值及其置信区间。例如:在农用药物的毒力测定中,药品浓 度是X变数,昆虫死亡率是Y变数,如欲得到半致死浓度(Y=50%时的药品浓度),就必须 从Y反推X:在树龄测定中,年轮数是X变数,“碳记年”是Y变数,由碳记年估计树木年龄 也是由Y反推X。很多仪表的校准(calibration)亦属由Y(仪表读数)预测X(标的物状况)。 在近代遗传学研究中,QTL的定位也是要从Y(表型值)估计X(基因座位位置)。这类从Y反 推、估计或预测X的分析,统称为逆回归或逆预测,其统计原理和方法国内尚未见报道。本 文将阐述逆回归的意义,推导其区间估计,并以实例说明演算过程,以供应用和深入理解某 些涉及逆回归的问题。文中所用符号和公式,除特别说明外,都按照文献[1],不再解释。 接受日期 0-09.25 Received on:2000-08-14.Accepted on:2000-09-25
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 第 "#卷 第 $期 作 物 学 报 %&’("#)*&($ "++,年 -月 ./0. .123*345/. 65*5/. 6789()"++, 线性回归分析的逆预测: 莫 惠 栋 ;扬州大学数量遗传研究室)江苏扬州 ""$++-的对应值 >+及其 ,++;, ?@+ }]zZ9y,++;,? ~ 固定)=随机B所以分析的基本目的是由 >估计或预测 =)其 *元线性回归模型的一般形式 为 =+,‘-.ah>h+-j+;h,,)")/)*D+,,)")/)f 值及其置信区间B例如2在农用药物的毒力测定中)药品浓 度是 >变数)昆虫死亡率是 =变数)如欲得到半致死浓度;=,$+A时的药品浓度D在树龄测定中)年轮数是 >变数)3碳记年4是 =变数)由碳记年估计树木年龄 也是由 =反推 >B很多仪表的校准;{}’Z#x}9Z&];标的物状况;基因座位位置的分析)统称为逆回归或逆预测)其统计原理和方法国内尚未见报道B本 文将阐述逆回归的意义)推导其区间估计)并以实例说明演算过程)以供应用和深入理解某 些涉及逆回归的问题B文中所用符号和公式)除特别说明外)都按照文献0,1)不再解释B : 国家自然科学基金;6-7#+6-,<项目资助 收稿日期2"+++[+8[,9)接受日期2"+++[+-["$ 27{7Zw7z&]2"+++[+8[,9).{{7897z&]2"+++[+-["$ 万方数据

546 作物学 报 27卷 1原理和公式 在一元线性回归中,Y依X的条件总体平均数x由 Y=a+bX % 估计;其对x的100(1-a)%置信带由 y士=y士[片+X (2) 给出。当 Y=Y。 (3) 时,以上3个方程的几何轨迹可见图1。图1上 3个交点所对应的X轴坐标值:X。表示对应于 Y。的X估计值:X和X分别表示对应于Y。 的X,的100(1一a)%可信限((fiducial limits)回 或逆置信限((inverse confidence limits)的低限 和高限。[X,X,]则称为逆回归的100(1 a)%可信区间或预测区间。 估计X。是方便的,因为根据(1)可有Y。=a +bX。,故 X。=(Y。-a)/b。 (4) 对于X和X的估计,可推导如下:低限X上 的“高度”Y可表示为: Y=Y。=a+bXo, (5) 图】逆回归的几何意义 和Y=a+bX-x+X-7 x。(6) Fig.】Geomerica or inverse regreo,令(5)=(6),并左右平方可得: i.e..predicting Xo.X and Xe given Yo x,-6xr=[片+] (7) 同理,对高限X“上的“高度”亦可得 (8) 上述(7)和(8)除X和X,的区别外,其余完全相同;若以X代X,或X,均可写成二次 三项式: AX:+BX+C=0. (9) A=b-tx/x2,B=2xtx/∑x2-2bX。 其中 (10) C=bXi-tisi/n-tisix/Ex2 因此,解(9)得到X的两个根即分别为X和X。 万方数 g=s号x/Bx (11) 化(10),再代回 (9)即可解得
! 原理和公式 在一元线性回归中"#依 $的条件总体平均数 %#&$由 # ’( )* +$ ,-. 估计/其对 %#&$的 -00,-12.3置信带由 # ’4 526# ’( # ’4 526#&$ - 7* ,$1 8 9.: 当 #( #0 ,?. 图 - 逆回归的几何意义 @ABC- DEFGEHIAJKLEMNLKOKHAFOPFIAOQEIREIEBIERRAFO" SCTC"NIEUAJHAOB$0"$V KOU$W BAQEO#0 时"以上 ?个方程的几何轨迹可见图 ->图 -上 ?个交点所对应的 $ 轴坐标值X$0表示对应于 #0的 $ 估计值/$V 和 $W 分别表示对应于 #0 的 $0的 -00,-12.3可信限,PAUYJAKLLAGAHR. 估计 $0是方便的"因为根据,-.可有 #0() *+$0"故 $0( ,#01 ).&+> ,Z. 对于 $V 和 $W 的估计"可推导如下X低限 $V 上 的[高度\#可表示为X #( #0( )* +$0" ,]. 和 #()*+$V1526#&$ - 7*,$V18 9.: ,^. 令,].(,^."并左右平方可得X ,+$01 +$V.:( 5: 26: #&$ - 7* ,$V 1 8 9.: ,_. 同理"对高限 $W 上的[高度\亦可得X ,+$01 +$W.:( 5: 26: #&$ - 7* ,$W 1 8 9.: ,‘. 上述,_.和,‘.除 $V 和 $W 的区别外"其余完全相同/若以 $代 $V 或 $W"均可写成二次 三项式X a$:* b$* c( 0> ,d. 其中 a(+: 15: 26: #&$&;8: "b(:85: 26: #&$&;8: 1:+: $0 c(+: $: 015: 26: #&$&718: 5: 26: #&$&;8 e f g : > ,-0. 因此"解,d.得到 $的两个根即分别为 $V 和 $W> 令 h( 5: 26: #&$&+: ;8: ,--. 简化,-0."再代回,d.即可解得X ]Z^ 作 物 学 报 :_卷 万方数据

5期 莫惠栋:线性回归分析的逆预测 Xx-图-x-a±01- (12 其中 d-[=®+] x2 (13) 2推户 上述是Y。为条件总体平均数4x的逆回归,可推广于 2.1Y。仅是Y的一个观察值的逆回归 由于Y的标准误为: =wx[1+}+-7 x2」 。 (14) 这一改变仅使应用(12)于估计X。和X时的d值改变为: d-[1-0+2] (15) 2.2Y。是m个Y值的平均值的逆回归 仍应用(I2)估计X。和X,但d改变为: d=名[品+1-)+-] (16) x2 2.3Y。是多元线性回归依变数的逆回归 上述原理和方法也可能推广到多元线性回归模型,这里只作概述。k元线性回归方程Y =a十b,X1十b2X2十…+bX的逆回归,即求Y=Y。时k维空间点(Xo,X0,…,X)的可信 区((fiducial region)。由于k元回归中Y和Y的标准误可以一般化地写作): s=5yxxX(X'X)-Xo] sy=yxx.x,1+X。(XX)-X]e了 (17) (17)中的X为X变数的nX(k十1)阶矩阵,X。为X的列向量,即X。=(1,Xo,X0,, X0)。而前述令(5)=(6)并左、右平方也可写成: [Y。-(a+bX)]=ts5。 (18) 故推广于k元回归时,若Y。是条件总体平均数X。,则X可信区的界面满足方程: [Y。-(a+bX1+bX2+…+bX)]=sx,m.x,[X(X'X)-1X]。 (19) 若Y。是单一观察值则满足方程: [Y。-(a+bX,+bX:+…+hX,)]=8xx-x[1+X,(X'X)-X,]。(20) 异常和原因 逆回归可能出现一些异常情况,例如:(1)X,和X,为复数,其几何图形是Y=Y。与置 信带的双曲线不相交,如图2(a):(2)X,和X,虽为实数,但其间不包含X。,如图2(b)。以 上逆回归显然都没有实际意义。其原因是回归的线性不强,使置信带双曲线迅速偏离回归直 线,以及测晚远离回归中心工。这可通过对g和(X。一五)的分析得到了解
!" !# ! $ % & (’ " )*!+, -./0 123*4, -/5 *46/ 其中 1"789:3! ; *4,-/ .6 2 436 ? *4@/ A 推广 上述是 :+为条件总体平均数 B:3!的逆回归5可推广于C ADE FG仅是 F的一个观察值的逆回归 由于 :的标准误为C 9: " 9:3! 4= 4 .6 2 436 ? *4H/ 这一改变仅使应用*46/于估计 !# 和 !( 时的 1值改变为C 1" 789:3! ; .6 2 436 ? *4J/ ADA FG是 K个 F值的平均值的逆回归 仍应用*46/估计 !# 和 !(5但 1改变为C 1" 789:3! ; 4 L = 4 M .6 2 436 ? *4O/ ADP FG是多元线性回归依变数的逆回归 上述原理和方法也可能推广到多元线性回归模型5这里只作概述?Q元线性回归方程 : R "S=;4!4=;6!6=T=;Q!Q的逆回归5即求 :":+时 Q维空间点*!4+5!6+5T5!Q+/的可信 区*UVWXYVZ[\]^V_‘/?由于 Q元回归中 : R和 :的标准误可以一般化地写作)@2 C 9: R" 9:3!45!65T5!Q)ab +*aba/,4 a+2436 9: " 9:3!45!65T5!Q)4= ab +*aba/,4 a+2 c & ’436 ? *4d/ *4d/中的 a为 ! 变数的 <e*Q=4/阶矩阵5a+为 !f+的列向量5即 ab +"*45!4+5!6+5T5 !Q+/?而前述令*J/"*O/并左g右平方也可写成C ):+, *S= ;!/26" 76 896 : R? *4h/ 故推广于 Q元回归时5若 :+是条件总体平均数 B:3!f+5则 !f+可信区的界面满足方程C ):+, *S= ;4!4= ;6!6= T = ;Q!Q/26" 76 896 :3!45!65T5!Q)ab +*aba/,4 a+2? *4i/ 若 :+是单一观察值则满足方程C ):+, *S= ;4!4= ;6!6= T = ;Q!Q/26" 76 896 :3!45!65T5!Q)4= ab +*aba/,4 a+2? *6+/ P 异常和原因 逆回归可能出现一些异常情况5例如C*4/!( 和 !# 为复数5其几何图形是 :":+与置 信带的双曲线不相交5如图 6*Z/j*6/!( 和 !# 虽为实数5但其间不包含 !+5如图 6*k/?以 上逆回归显然都没有实际意义?其原因是回归的线性不强5使置信带双曲线迅速偏离回归直 线5以及预测的 !+远离回归中心 .?这可通过对 -和*!+,./的分析得到了解? J期 莫惠栋C线性回归分析的逆预测 JHd 万方数据
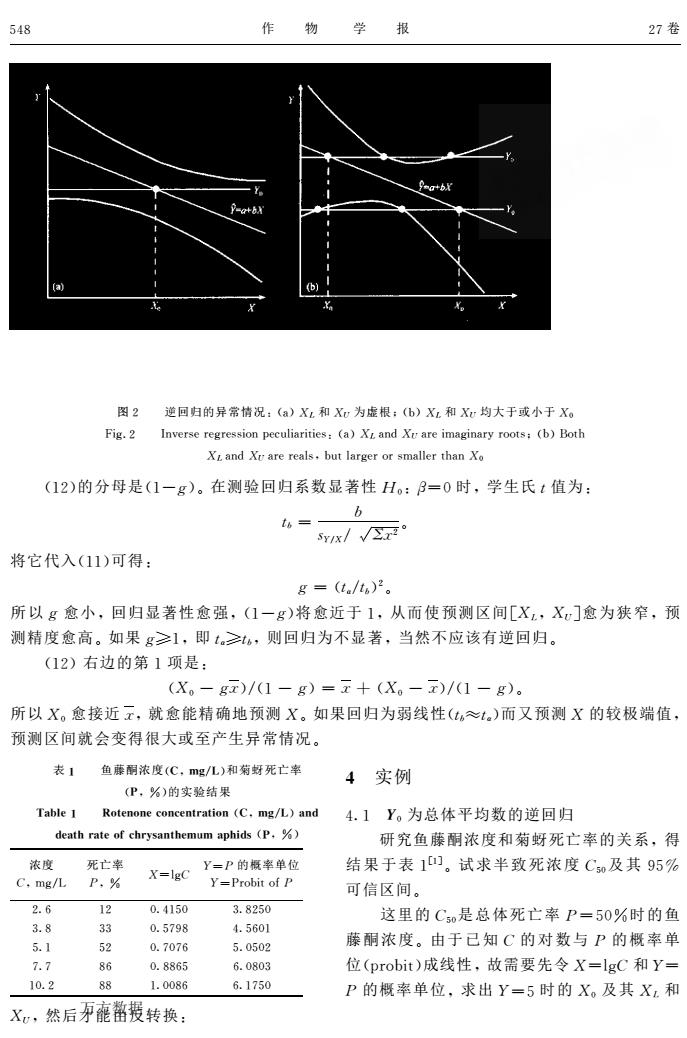
548 物 学 27卷 图2逆回归的异常情况:(a)X和X为虚根,(b)X和Xr均大于或小于X。 Fig.2 Inverse regression peculiarities:(a)X and X are imaginary roots (b)Both Xt and Xr are reals.but larger or smaller than Xo (12)的分母是(1一g)。在测验回归系数显著性H。:B=0时,学生氏1值为: w= Synx/x 将它代入(11)可得: g=(t./ts)2。 所以g愈小,回归显著性愈强,(1一g)将愈近于1,从而使预测区间[X,X]愈为狭窄,预 测精度愈高。如果g≥1,即t≥4,则回归为不显著,当然不应该有逆回归。 (12)右边的第1项是: (X。-gz)/(1-g)=五+(X。-x)/(1-g)。 所以X。愈接近云,就愈能精确地预测X。如果回归为弱线性(≈)而又预测X的较极端值, 预测区间就会变得很大或至产生异常情况。 表】鱼藤浓度(C,mg/L)和菊蚜死亡率 4实例 (P,⅓)的实验结果 Table 1 Rotenone concentration (C.mg/L)and 4.1Y。为总体平均数的逆回归 death rate of chrysanthemum aphids (P.%) 研究鱼藤酮浓度和菊蚜死亡率的关系,得 浓度 死亡率 y三P的概率单位 X=lgC 结果于表1。试求半致死浓度C及其95% C,mg/LP,⅓ Y=Probit of P 可信区间。 2.6 12 0.4150 3.8250 3.8 .560 这里的C是总体死亡率P=50%时的鱼 5.1 藤酮浓度。由于已知C的对数与P的概率单 0.7070 5.0502 7.7 86 0.8865 6.0803 位(probit)成线性,故需要先令X=lgC和Y= 10.2 88 1.0086 6.1750 P的概率单位,求出Y=5时的X。及其X和 X,然后界能蕃授转换:
图 ! 逆回归的异常情况"#$%&’和 &( 为虚根)#*%&’和 &( 均大于或小于 &+ ,-./! 012345343.4355-617389:-$4-;-35"#$%&’ $1466;5)#*%?6;@ &’ $1<&( $4343$:5A*9;:$4.34645=$::34;@$1&+ #B!%的分母是#BCD%E在测验回归系数显著性 F+"GH+时A学生氏 I值为" IJH J KLM&MPNO!E 将它代入#BB%可得" DH #IQMIJ%! E 所以 D愈小A回归显著性愈强A#BCD%将愈近于 BA从而使预测区间R&’A&(S愈为狭窄A预 测精度愈高E如果 DTBA即 IQTIJA则回归为不显著A当然不应该有逆回归E #B!%右边的第 B项是" #&+C DO%M#BC D%H OU #&+C O%M#BC D%E 所以 &+愈接近 OA就愈能精确地预测 &E如果回归为弱线性#IJVIQ%而又预测 &的较极端值A 预测区间就会变得很大或至产生异常情况E 表 W 鱼藤酮浓度#XAYZM[%和菊蚜死亡率 #\A]%的实验结果 ^_‘abW cdebfdfbgdfgbfeh_eidf#XAYZM[%_fj jb_ekh_ebdlgkhmn_fekbYoY _pkijn#\A]% 浓度 qA=.Mr 死亡率 sA] &H:.q LHs的概率单位 LHt46*-;6us !/v B! +/wBx+ y/z!x+ y/z yy +/x{|z w/xv+B x/B x! +/{+{v x/+x+! {/{ zv +/zzvx v/+z+y B+/! zz B/++zv v/B{x+ } 实例 w/B ~+为总体平均数的逆回归 研究鱼藤酮浓度和菊蚜死亡率的关系A得 结果于表 BRBS E试求半致死浓度 qx+及其 |x! 可信区间E 这里的 qx+是总体死亡率 sHx+]时的鱼 藤酮浓度E由于已知 q的对数与 s的概率单 位#746*-;%成线性A故需要先令 &H:.q和 LH s的概率单位A求出 LHx时的 &+及其 &’ 和 &(A然后才能由反转换" xwz 作 物 学 报 !{卷 万方数据

5期 莫惠栋:线性回归分析的逆预测 549 C=anti le x 得到C等。 从表1的X和Y得到:z=0.7195,y=5.13812,x2=0.223846,y2=4.028944,xy =0.938747,Y=2.120737+4.193721X,5yx=0.175216。查t表,df=5-2=3时,ts= 3.182。因此,根据(4)、(11)、(13)和(12)依次有: X。=(5-2.120737)/4.193721=0.686565, g=(3.1822×0.1752162)/(4.1937212×0.223846 =0.078959 d=3.182×0.1752161-0.078959+0.686565-0.7195)27 4.193721 0.223846 =0.057805 X。=[(0.686565-0.078959×0.7195)+0.057805]/(1-0.078959)=0.746502, X=[(0.686565-0.078959×0.7195)-0.057805]/(1-0.078959)=0.620981 以上结果说明:鱼藤酮对菊蚜的半致死浓度为 表2 水流流率(X,m3/see)】 Cso=antilg0.686565=4.86mg/L;其95%可信高限 和流率仪读数(y) 为antilg0.746502=5.58mg/L,低限为antilg Table 2 Flow rate (X.m2/sec) 0.620981=4.18mg/L。 and readings on a flow meter (Y) 4.2Y。为单一观察值的逆回归 y 研究灌溉水流率和流率仪读数的关系,得表2结 果。某次测定读得Y。=4.0,求流率X。及其95%可 信限。 4.2 从表2可得回归分析的基本数据:x=5.5,y= 5.8 5.45,x2=82.5,y2=67.065,xy=74.35和Y= 6.8 7.6 0.493333+0.901212X,sx=0.086503。df=8时的 8.7 as=2.306。故根据(4)、(11)、(15)和(12)依次有: 10 9.5 X。=(4.0-0.493333)/0.901212=3.8911m3/sec, g=(2.3062×0.0865032)/(0.9012122×82.5)=0.000594, -2306X0.086503TLX0.909406士③.8911-5.5)7 0.901212 82.5 =0.2354 X。-g元=3.8911-(0.000594×5.5)=3.8878, 所以,X=(3.8878+0.2354)/0.999406=4.1256m3/sec, X=(3.8878-0.2354)/0.999406=3.6546m3/sec。 参考文献 1莫惠栋.农业试验统计.上海:上海科学技术出版社,1992.308~329,510~526 2 Williums EJ.Regression Analysis.New York:John Wiley 8.Sons.Inc..1959.Chapt.6 3 Draper N R.H Smith.Applied Regression Analysis.New York:John Wiley &Sons.Inc..1998.47~51 4 Ott R L.An introduction to statistical Methods and Data Analysis.Belmont.California:Duxbury Press.Wadsworth Inc.,1993.437-563 XXX万右数据XX和和
!" #$%&’() 得到 !*+等, 从表 -的 )和 .得到/0"+12-3*45"*1-67-84908 "+18867:;4958 ":1+873::4905 "+13672:24. .?)"+1-2*8-;,查 @表4AB"*C8"6时4@+1+*" 61-78,因此4根据D:EFD--EFD-6E和D-8E依次有/ )+" D*C 81-8+262E?:1-3628-" +1;7;*;*4 G" D61-788H +1-2*8-;8 E?D:1-3628-8H +18867:;E" +1+273*34 A" 61-78H +1-2*8-; :1-3628- -C +1+273*3 * = D+1;7;*;*C +12-3*E8 I +18867:; J -?8 " +1+*27+*4 )K " ID+1;7;*;*C +1+273*3H +12-3*E= +1+*27+*J?D-C +1+273*3E" +12:;*+84 )L " ID+1;7;*;*C +1+273*3H +12-3*EC +1+*27+*J?D-C +1+273*3E" +1;8+37-, 表 M 水流流率DN4OP?QRSE 和流率仪读数DTE UVWXRM YXZ[\V]RDN4OP?QRSE V^_\RV_‘^aQZ^VbXZ[OR]R\DTE ) . - -1: 8 816 6 61- : :18 * *1- ; *17 2 ;17 7 21; 3 712 -+ 31* 以上结果说明/鱼藤酮对菊蚜的半致死浓度为 !*+"#$%&’(+1;7;*;*":17;c(?de其 3*f可信高限 为 #$%&’( +12:;*+8" *1*7c(?d4低 限 为 #$%&’( +1;8+37-":1-7c(?d, g1M Th为单一观察值的逆回归 研究灌溉水流率和流率仪读数的关系4得表 8结 果I:J ,某次测定读得 .+":1+4求流率 )+及其 3*f可 信限, 从表 8可得回归分析的基本数据/0"*1*45" *1:*4908 "781*4958 ";21+;*4905"2:16*和 . .?)"+1+7;*+6,AB"7时的 @+1+*"816+;,故根据D:EFD--EFD-*E和D-8E依次有/ )+" D:1+C +1:36666E?+13+-8-8" 6173--c6 ?ijk4 G" D816+;8H +1+7;*+68 E?D+13+-8-88H 781*E" +1+++*3:4 A" 816+;H +1+7;*+6 +13+-8-8 --H +1333:+; -+ = D6173--C *1*E8 I 781* J -?8 " +186*:4 )+C G0" 6173--C D+1+++*3:H *1*E" 6177274 所以4 )K"D617727=+186*:E?+1333:+;":1-8*;c6 ?ijk4 )L"D617727C+186*:E?+1333:+;"61;*:;c6 ?ijk, 参 考 文 献 - 莫惠栋1农业试验统计1上海/上海科学技术出版社4-33816+7l6834*-+l*8; 8 m&’’&nciop1qrGsr>>tuvwvxy5>t>1zj{|}~!/p}"$m&’j#$%}$i4&$k14-3*31’"#(%1; 6 )~#(j~z *4+ %c&%"1w,,ytrAqrGsr>>tuvwvxy5>t>1zj{|}~!/p}"$m&’j#$%}$i4&$k14-3371:2l*- : -%%* d1wvtv@suA./@tuv@u>@x@t>@t/xy0r@1uA>xvA2x@xwvxy5>t>13j’c}$%4’#’&4}~$&#/)n56n~#7~jii4m#8i{}~%" &$k14-3361:62l*;6 )K )K )K )K )K )K)K )K )K *期 莫惠栋/线性回归分析的逆预测 *:3 万方数据

线性回归分析的逆预测 日万方散据支成装秋 作者: 莫忠栋 作者单位: 扬州大学数量遗传研究室 刊名 作物学报STIC PK) 燕文刊名: ACTA AGRONOMICA SINICA 年,卷(期 201,276 引用次数 0 老考文就条) L.莫惠栋衣业试验统计1992 2.Williums E J Regression Analysis 1959 3.Draper N R.H Smith Applied Regression Analysis 1998 4.0tt R L An introduction to statistical Methods and Data Analysis 1993 相似文然L条) 1学位论文莫里桑卡ory Sangare中国南方地区奶牛泌乳曲线数学模型的研究?05 月龄、次。产季节影响效应。采用简单线性国归对不同胎次、季节、测定日的产奶量进行位正,利用S软件进行分析。并且 多项式型的参数: 研究结果表明,对测定日产奶量有影响品P多项式型02 国归模型(022150>多项式模型(02120:第 多项式模型0.8113)>逆回白模型0.736170 第2始: 多项式模型(0.77)>逆回归模型(0.745 第3: 多项式模生 >回归型0过 22)>道 型(0.9 99s76>多项式模型(0.9940 无论是对季节进行校正 说明用光处之后能更好归地拟合广州奶牛的常曲线而且乳线的店以经过光清方法之后所 合的为准 本文链接:http:/dg.anfangdata,com,cn/Periodical_zuowxb20010500L,asp
线性回归分析的逆预测 作者: 莫惠栋 作者单位: 扬州大学数量遗传研究室, 刊名: 作物学报 英文刊名: ACTA AGRONOMICA SINICA 年,卷(期): 2001,27(5) 引用次数: 0次 参考文献(4条) 1.莫惠栋 农业试验统计 1992 2.Williums E J Regression Analysis 1959 3.Draper N R.H Smith Applied Regression Analysis 1998 4.Ott R L An introduction to statistical Methods and Data Analysis 1993 相似文献(1条) 1.学位论文 莫里·桑卡雷(Mory Sangare) 中国南方地区奶牛泌乳曲线数学模型的研究 2005 本研究利用广州市奶牛研究所奶牛场2000~2005年间1469头荷斯坦奶牛5863条泌乳记录,利用SAS软件ProcREG过程来估计产犊 月龄、胎次、产犊季节影响效应。采用简单线性回归对不同胎次、季节、测定日的产奶量进行校正,利用SAS软件进行分析,并且 对原始数据进行了Lowess光滑预处理,对不同模型分别采用SAS软件ProcREG和ProcNLIN计算模型参数,利使用多项式回归模型和 Ali等(1987)年提出的逆回归模型对泌乳曲线进行了拟合,采用SAS软件ProcNLIN计算逆回归模型的参数,利用ProcREG过程来计算 多项式模型的参数。 研究结果表明:对测定日产奶量有影响显著(P<0.01)的因素包括胎次、产犊月龄和产犊季节。各因子 每测定日产奶量的回归系数平均分别为:胎次(0.6043319)、产犊月龄(0.003670)、产犊季节(0.4966133),产犊月龄的回归系数是 最低,比其它因子影响小,表明本研究的产犊月龄划分是可行的。产犊月龄、产犊季节与测定日产奶量的回归分析结果表明:各胎 次的回归系数都达极显著水平(P<0.01),但是各胎次产犊季节的回归系数都大于产犊月龄的。产犊月龄(变量X1)和产犊季节(变量 X2)每次测定的泌乳量的回归系数平均分别为:第一胎X1为-0.03880、X2为0.856937;第二胎X1为-0.026478、X2为0.123124;第三 胎X1为-0.0458519、X2为0.09049;第四胎X1为-0.187895、X2为1.43744。各个胎次的X2(产犊季节)的回归系数都高于X1(产犊月龄 ),说明各胎次产奶量受产犊季节的影响最大。 利用本研究的原始数据进行泌乳曲线的拟合时,所有模型的拟合度(R2)都只 有0.157094~0.357969左右。对产犊季节进行简单线性回归和光滑(Lowess)处理后,回归曲线的拟合度显著升高,例如第四胎次的 逆回归模型在未对产犊季节校正之前R2=0.357969,对产犊季节校正后R2=0.870970;同样,该模型在未经过光滑处理之前 R2=0.357969,光滑处理之后R2=0.998761。通过光滑处理之后,无论是逆回归模型或多项式回归模型,光滑处理之后的R2都高于简 单线性回归校正之后的R2,说明对广州地区奶牛产奶量校正方法,Lowess方法要比传统的简单线性回归方法好,更具有科学性。本 研究用SAS的PROCREG和SAS软件PROCNLIN两种方法计算的结果表明,PROCREG方法的(R2)普遍都高于PROCNLIN方法,多项式模型 (PROREG)的提高幅度(不同胎次校正数据的结果平均提高0.5626)要高于逆回归模型(NLIN,平均提高0.514733);同样,经过光滑处 理之后,PROCREG方法的(R2)普遍都高于PROCNLIN方法,逆回归模型提高幅度(不同胎次光滑数据的结果平均提高0.727311)要低于 多项式模型(平均提高0.728125)。两个模型经过光滑处理对季节校正之后的提高幅度增加,说明PROCREG方法更能准确处理季节校 正和光滑处理之后的数据。未作季节校正数据经光滑处理前,多项式模型在1、2、3、4胎次的残差均方分别为24.96666、 34.29267、36.43438及35.93795,相应地逆回归模型的残差均方在24.9710~36.3667之间。对季节进行校正之后,各模型在胎次间 残差均方的差异不大,多项式模型在1、3、4胎分别为1.80051、3.15096及2.99703,相应地逆回归模型在1~4胎的残差均方在 2.9639~6.0232之间。经过光滑处理之后,各模型胎次间的残差均方相差不大,多项式模型在1、2、4胎次的残差均方分别为 0.00354、0.00516及0.01276,逆回归模型1~4胎的残差均方在0.0265~0.0781之间。经光滑之后,多项式模型和逆回归模型的残 差均方比简单线性回归小得多,表明光滑处理能够较大幅度地提高模型的拟合度。 研究表明不同胎次不同模型泌乳量的拟合 效果的R2排名如下: 未对季节校正数据和未经过光滑处理的数据:第1胎:多项式模型(0.15750)>逆回归模型 (0.15709);第2胎:逆回归模型(0.28985)>多项式模型(0.28950);第3胎:逆回归模型(0.282150)>多项式模型(0.28120);第 4胎:逆回归模型(0.357969)>多项式模型(0.35740)。总体上逆回归模型的拟合效果好。 对季节进行校正之后的数据:第 1胎:多项式模型(0.8113)>逆回归模型(0.736170);第2胎:多项式模型(0.7497)>逆回归模型(0.745089);第3胎:多项式模型 (0.8113)>逆回归模型(0.793808);第4胎:逆回归模型(0.870970)>多项式模型(0.8696)。 经过光滑处理的数据:第1胎 :多项式模型(0.99920)>逆回归模型(0.999188);第2胎:多项式模型(0.99960)>逆回归模型(0.999238);第3胎:多项式模型 (0.999222)>逆回归模型(0.999222);第4胎:逆回归模型(0.9998761)>多项式模型(0.99940)。 无论是对季节进行校正之 后或经过光滑处理数据,所有情况下多项式模型的拟合效果最好,但是经过光滑处理之后的各模型R2都高于经过简单线性回归校正 之后的R2,说明用光滑处理之后,能更好回归地拟合广州荷斯坦奶牛的泌乳曲线,而且泌乳曲线的拐点应以经过光滑方法之后所拟 合的为准。 本文链接:http://d.g.wanfangdata.com.cn/Periodical_zuowxb200105001.aspx

下载时间:2010年3月5日
下载时间:2010年3月5日