
Journal of 生物数学学报2001,16(3):341-347 Biomathematics 非平衡群体基因变异测量的Shannon信息量方法 郭满才宋世德周静芋袁志发 (西北农林科技大学生命科学学院。陕酒杨液71210) 物要:在Shannon告怎重的益出上,对非平街群体建立了年体基因型相对信怎量S1G. 纯合体相对信息量S(G、杂合体和对信息量SHG)的鞭念,并《子它们以遭传学惠义.与基 一度」和基多样度D选了理论比权,结采明,二者在数量规上有很好的一此性 应又无构时做立的指标件系,且各构时雪8量还有新的内话。S©)就能表丛泰因定异,又镜 反映基日型水平上的道传变异,S(G)主要反块纯合体的违传变养,S(G)主要反映杂合体的 遗传变异。各相对信怎量既可反唤年保的造传变异位度,又能比枝不网位点问的通传变异很度。 关键词非平衡年体:Shanne0n信息量,基因一其度:基园多样定:年体基因型任怎量 中图分类号:S813.1MR分类号:20B30;92D20 文献标识码:A 文童编号:1001-96262001103034107 如何定量地描述非平衡群体的基因变异,N刊认为在非随机交配群体中,虽然杂合度与 群体内杂合体的颜率无关,不过它仍然是一个群体内基因变异的理想尺度,可以适用于任何生 物,无论是自体受精生物还是异体受精生物;是单倍体还是多倍体.并建议对这些生物,把杂 合度H改称为“基因多样度”,纯合度J改称为“基因一致度”, Weir网在论述基因多样性时 也沿用同样的指标.。但实际上,对于非平衡群体,这种描述只利用了基因库须率而没有利用基 因型领率.1998年袁志发等提出用相对Shannon信息量描述平衡弹体的基因变异问,并赋 予它们以遗传学意义.本文拟研究非平衡群体基因变异的Shannon信息量测量方法,并与基 因多样度进行比较研究,对定量描述群体的基因变异提供-一种新的方法,以使Sha1o加信息其 方法得到更好的应用. 基因多样度D)及其性质 设复等位基因位点A为 (A1,A2,Ax)=(B,P,,Px) 其中乃为A,的额率,R≥0,且公P=1.其对应的群体在理论上有无穷多个,不失一般 安精日期:1999-08-15 作者简介:郭情才(1963-),男。陕西宝鸡人,西北农林科技大学生印科学学院碳士 万方数据
生物数学学报2001,16f31:341 347 JournaI of Biomathematics 非平衡群体基因变异测量的shannon信息量方法 郭满才 宋世德 周静芋 袁志发 (西北农林科技大学生命科学学院,陕西杨陵7121001 摘要:在shannon信息量的基础上,对非平衡群体建立了群体基因型相对信息量s。(G). 纯舍体相对信息量sj(G)、杂合体相对信息量s备(G)的概念,并赋予它们以遗传学意义与基 因一致度J和基因多样度D进行了理论比较,结果表明,二者在数量规律上有很好的一致性, 但又是相对独立的指标体系,且各相对信息量还有新的内涵. S。(G)既能表征基因变异,卫能 反映基因型水平上的遗传变异,sj(G)主要反映纯合体的遗传变异,s岛(G)主要反映杂合体的 遗传变异各相对信息量既可反映群体的遗传变异程度,又能比较不同位点问的遗传变异程度. 关键词:非平衡群体;shannon信息量;基因一韭度;基因多样度;群体基因型信息量 中圈分类号:S813 l MR分类号:20830;92D20 文献标识码:A 文章编号:lool一9626(2001)03一034l—07 如何定量地描述非平衡群体的基因变异,Nc·【1】认为在非随机交配群体中,虽然杂合度与 群体内杂合体的频率无关,不过它仍然是一个群体内基因变异的理想尺度,可以适用于任何生 物,无论是自体受精生物还是异体受精生物;是单倍体还是多倍体.并建议对这些生物,把杂 合度Ⅳ改称为“基因多样度”,纯合度,改称为“基因一致度”.weir【4】在论述基因多样性时 也沿用同样的指标.但实际上,对于非平衡群体,这种描述只利用了基因库频率而没有利用基 因型频率. 1998年袁志发等提出用相对shannon信息量描述平衡群体的基因变异【5】,并赋 予它们以遗传学意义.本文拟研究非平衡群体基因变异的shannon信息量测量方法,并与基 因多样度进行比较研究,对定量描述群体的基因变异提供一种新的方法,以使sha,·n。n信息鼍 方法得到更好的应用. 1 基因多样度D【-】及其性质 设复等位基因位点A为 (A】,A2 ,J4Ⅳ)=(|DI,P2, ,PⅣ K 其中只为J4。的频率,只≥o,且∑只=1其对应的群体在理论上有无穷多个,不失一般 z=1 收稿日期:1999—08—15 作者简介:郭清才(1963一),男,陕西宝鸡人,西北农林科技大学生命科学学院副教授.硕士 万方数据

342 生物数学学报 第16卷 性,设它们为 (AA,A2A..AKAK:AA2.A1A3Ag-1AK) =(D1,D2,,DK,2,H13,…,HK-,K) 2② 其中纯合基因型AA有K个,频率为D,杂合基因型A4任<)有K(K-1/2个,频 本为,显然言D+=1共有基因型K(K+/2种 基因库(1)或群体(2)的基因一致度J和基因多样度D分别定义为 J=∑.D=1- (3) 其性质为 0sDsK1 当B之一等于1而其余均为0时,有hm=1,D=0:当乃均等于时,有an= 三D=K1显然.基因一致度J与多样度D分别是以平衡群体的纯合体频率与杂合 体频率为代表来度量具有同一基因库的任一群体的基因变异, 2非平衡群体相对信息量及其性质 当群体(②)不平衡时,其Shannon信息量定义为 O=-Dh+∑aH 群体的纯合体信息量S,(G)和杂合体信息量SH(G)分别定义为 S(C)=D.In D.5n(G)=-Hgla (6 则有 0≤SG=Sg+Sm1GshK+卫 (0 2 当群体中只有一种基因定时SG=0:当优+少种基因型颜米相等,且均为不可 时SGa=hK+,此时 sg=子h,sq- 2 由于(②的不平衡性,5SG)与S(以及SG的最大值不在同一点取得,结论如下(证明 当K≥3时 万方数据
万方数据

第3期 郭清才等,丰平衡群体落因变异测魔的Shannon信息基方法 343 其中当D皆等于京时5Gmm=hK:当风,皆等于-可时,5n(G= nK5-】0,或之一为1,其余为0时,它们均取最小值0 当k=2时 0≤SG)s, 0sSmG)≤ 其中当D=h=时,SGmw=是;当i=时,Su(G)a=是当D,D之-为 1,另-个为0时(Gmm=0,当H12=1时,SH(Gmn=0, S'(G,S(G)和Sa(G分别为群体的相对信息量,纯合体相对信息量和杂合体相对 信息量,则k≥3时 SJG) ≤G=b-n (10 (11) S(G) 0(G)-(G)+S(G)sI (12 当=2时,由(),(9)可得与(0)-(12类似的式子. SG的遗传学意义为群体(②的不背定性大小,S(G)表示纯合体的不肯定性大小, S(G)为群体的不肯定性程度,5分(G)为纯合体的不肯定性程度,即占最大可能不肯定性的比 例.SH(G与SH(G)可仿此解释. 对于具有多个位点的非平衡群体,可建立相应的平均信息最与平均相对信息量 3模拟结果与分析 对上述理论结果,在长=2时进行计算机模拟。A1的初始领率为0.0,步长0.1,终止频 率10,基因型率步长为0.05时模拟了511个群体A的初始额率0.00,步长0.01,头 止频率0.50,基因型频率步长为0.005 时模拟了2601个群体.用豆,S(G),Sa(G与S(G)分 别表示具有同一基因库的所有模拟群体杂合体频率 ,的平均值,纯合体相对信息#G 的平均值,杂合体相对信息量Sa(G的平均值以及相对信息量S'G)的 平均值。模拟结果与 理论结果完全相符(如最大值、最小值、最大值点、最小值点等),对模拟结果进行统计 得出如下有意义的结 (部 分数据见表1-表5,表4、表5为表1数据计算结果.其余略 )同一基因库的每一模拟群体,只要三种基因型的频率均不小于0.03,则其S(G,G。 5SG分别与该库的S(©,S(G,S#(G)差异不显著 2)D与月的关系为:当A1的颗率在0.0,0.061,0.47,0.531,0.94,1.00范围内时,二者差 异不显著。对其它基因库,二者有显著或极显著的差异,且D与月相比偏大: 3)D与(G)的关系为 当A1在0.00,0.03]及0.97,1.00范围内时,二者差异不显著。 对其它基因库,二者差异显著或极显著,且D与S(G)相比偏小.户与S(G)有与之完全类 似的性质. 万方数据
第3期 郭满才等;非平衡群体基因变异测量的shannon信息量方法 其中当。,皆等于去时s,(G)m。。=lnK;当皿,皆等于志时, sH(G)…= ln竺呸÷旦D:或爿玎之一为1,其余为。时,它们均取最小值。 当^=2时 o≤s,(G)s i o s sH(G)曼÷ 其中当D。=仍=÷时,曲(G)…=;;当Jv-z=:时,跏(G)。ax=:当D·,Dz之一为 j,另一个为。时曲(G)m。。=o,当Ⅳ12=l时,sH(G)删。=o 定义s’(G),彤(G)和s0(G)分别为群体的相对信息量,纯合体相对信息量和杂合体相对 信息量,则☆≥3时 ㈣”,2器s尚 Ⅲ拍,=器墨牟 唧悱尚划G)+郫)<l f10) (12) 当^=2时,由(7),(9)可得与(1【))一(12)类似的式子. s(G)的遗传学意义为群体(2)的不肯定性大小, s,(G)表示纯合体的不肯定性大小. s7(G)为群体的不肯定性程度,s,(G)为纯合体的不肯定性程度,即占最大可能不肯定性的比 例. sH(G)与s鲁(G)可仿此解释. 对于具有多个位点的非平衡群体,可建立相应的平均信息量与平均相对信息量. 3模拟结果与分析 对上述理论结果,在k=2时进行计算机模拟.A,的初始频率为0 o,步长o 1,终止频 率l O,基因型频率步长为0 005时模拟了511个群体.Al的初始频率0 00,步长o 01,终 止频率ojo,基因型频率步长为o 005时模拟了2601个群体.用H,$(G),s备(G)与s7(G)分 别表示具有同一基因库的所有模拟群体杂合体频率Ⅳ12的平均值,纯合体相对信息量昌(G) 的平均值,杂合体相对信息蹙50(G)的平均值以及相对信息量s7(G)的平均值.模拟结果与 理论结果完全相符(如最大值、最小值、最大值点、最小值点等)对模拟结果进行统计分析, 得出如下有意义的结果(部分数据见表1一表5,表4、表5为表L数据计算结果.其余略) 1)同一基因库的每一模拟群体,只要三种基因型的频率均不小于o 03,则其s’(G),昌(G) s二(G)分别与该库的s7(q,乃(G),%(G)差异不显著. 2)D与曰的关系为:当Al的频率在fo 00,o 06],[o 47,o 5 3】,[o 94,1.00]范围内时,二者差 异不显著.对其它基因库,二者有显著或极显著的差异,且D与H相比偏大. 3)D与雪’(G)的关系为:当A。在(0 oo,o 03]及[o 97:l 00]范围内时,二者差异不显著. 对其它基因库,二者差异显著或极显著,且D与s7(G)相比偏小. H与s 7(G)有与之完全类 似的性质. 万方数据
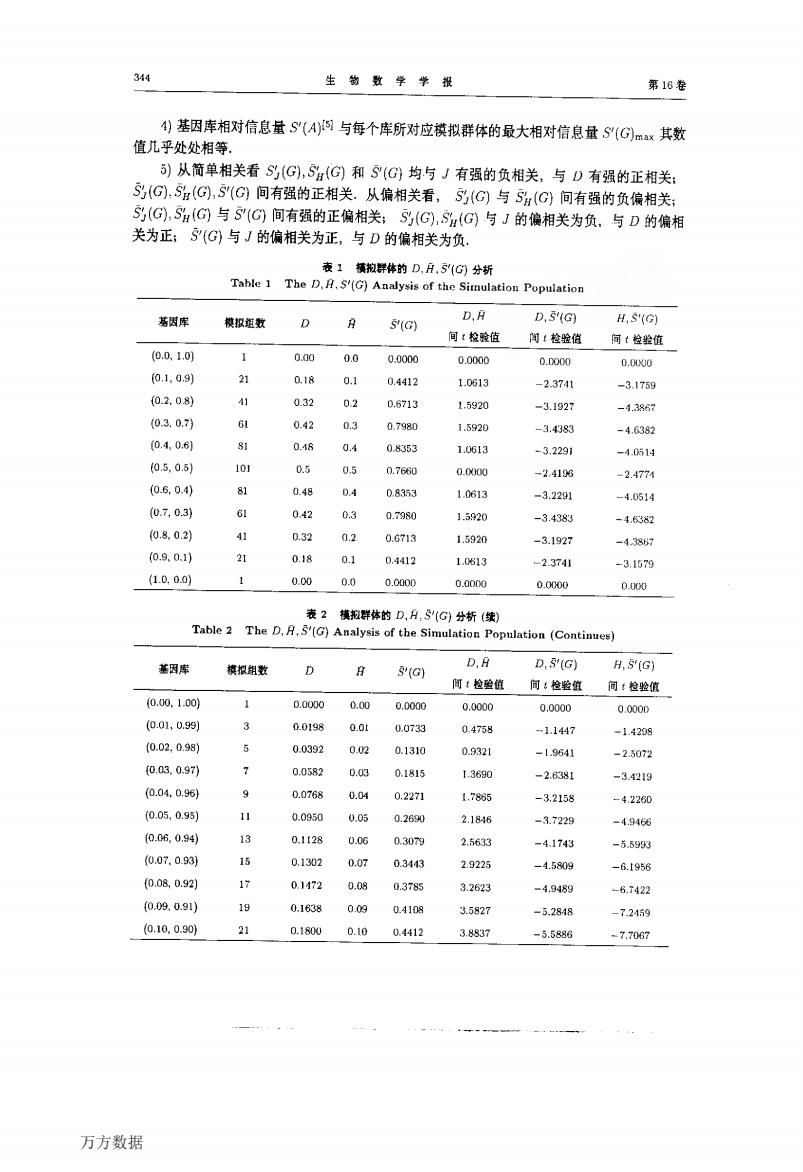
34 生箭数学学报 第16卷 4)基因库相对信息量S(A)网与每个库所对应模拟群体的最大相对信息量S(G)x其数 值儿乎处处相等. )从简单相关看S(G,S(G和S(G均与J有强的负相关,与D有强的正相关: 5(G).5(©,S"(G间有强的正相关.从偏相关看 S到1G与Sn(G,间有强的负偏相关: S(G,S(G与S(G间有强的正偏相关5乃1G,S4(G)与J的偏相关为负,与D的偏相 关为正: S(G)与J的偏相关为正,与D的偏相关为负. 横拘群体的D,户,5C分桥 S'(G)Analysis of the Simulation Population 葛因库 D S(G) D,S'(G) H,S(的 可‘检酸值 闻4粒验值 简:检验值 0.00 0.0 0.0000 0.0000 0.0m00 0.00 01,09) 21 0.18 0.1 0.4412 10%13 -2.374 -31759 0.2.081 0.32 02 06713 15920 -3192 -1386 03.0.7 0.42 0.798 1.5920 -3.4083 -4.6381 0405 0. 0.4 0.8353 1.0613 -3.2291 -40514 (05,05 10 0.5 0.76 -4108 -24774 06.0.4) 8】 0.4 1613 -322 -1051 0.7.0.31 3 0 1.592 -34383 -48382 0802 0.32 0.G713 1.5020 -3.1927 -d3867 (09.0.1 21 0.18 0.4412 1.0513 -23741 -3159 (1.0.0.0) 0.00 0.0 0.00 0.000 D.0C0 cion (Continues) 因库 横和组数 0 D,S'(G) H,'(G 间:检验 间:检验值 .0.1.0间 0.000 0.o 0.000 0.0000 0,0000 0.0000 0.01,0.9 0.0198 0.0t 00735 0.458 -1144 -1.4238 0.02,098 0.0392 0.02 0.1310 0.932 -19641 2.5072 0.03.0.97 0.0582 o. 13690 -26 0.04.096 -3.4219 0.076 0.01 0,2271 1.786 -3.2138 -4.2250 0.05,095 0.0050 0.05 0.2690 2.184 -372 -49465 0.06.094 0.1128 0.06 0.307 2563 -41743 5g (0.07.0.93 0.1302 2022 -1580 -6.195 0.147 0.09 0.378 3.262 -4.8489 -67422 (0.09.0.91 19 0.1638 003 0.4108 3.582 -32848 -7.24150 0.10,0.90j 21 0.180U 0.10 Q412 337 -5.5886 -7.700 万方数据
万方数据
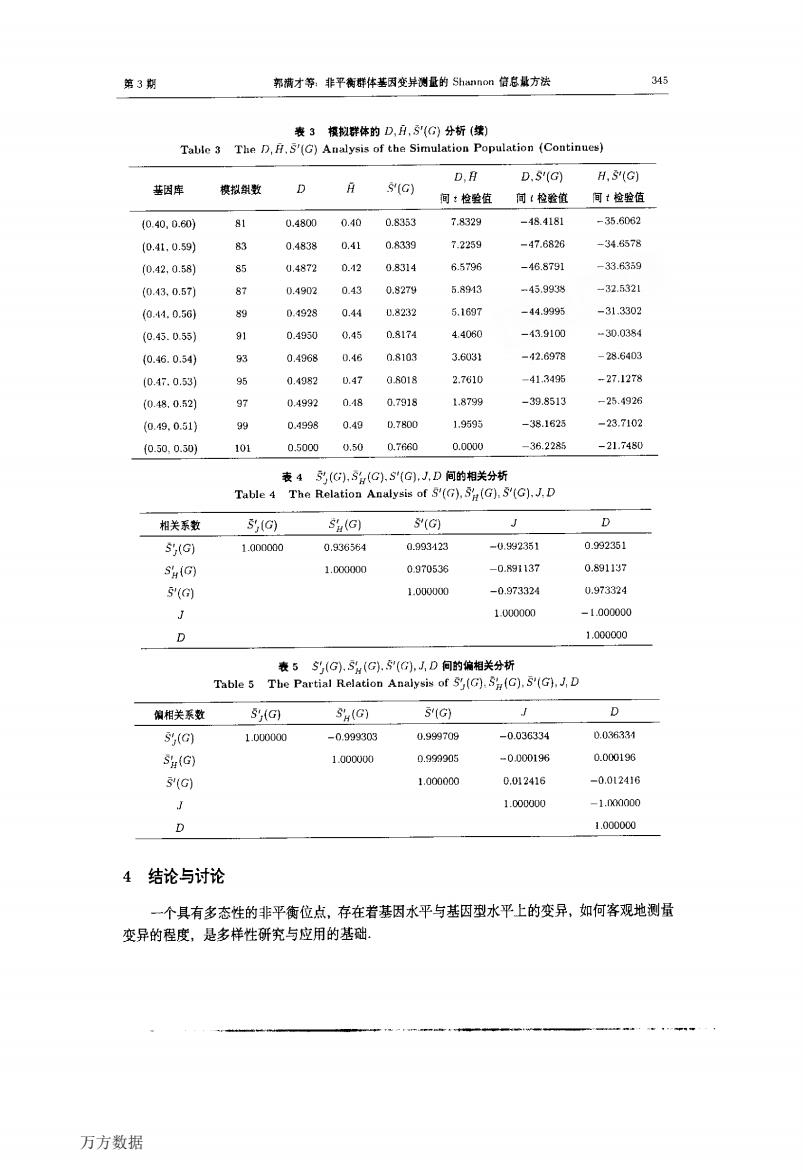
剪3期 郭满才等非平衡群体基因变量的Shannon倍方法 制体的D..G1分析 D.B D.S'(G) H,(G) 模拟织数 D G 间:检验值间:松验值阁1检验值 (0.40,0.60) a.4800 00 08353 78329 356032 (0.41.0.59) 83 04838 0.41 0.8339 72258 -47682到 -34657 0.42,0.58) 85 04872 012 0&314 6.5796 .465791 -33.8359 (043.0.5) 87 04902 0.827y 593 45.993 -32.532 (0.44.0.30 028 -49 -313302 (0.43.0.55) 91 0.4950 0.45 0.817 4.06 -43.9100 -30098 0.46.05 0.4968 046 nR103 3.6031 -42.6978 286403 04.03) 0018 2.7610 413195 27.1278 (0.48.0.52】 97 0493 1879 -39513 25.926 (049.0.51) 99 0.4508 0.40 D.7800 1.959 -38.1625 -237102 10.50.0.50 101 0.5000 0.500.70 0.0000 -36.2285 -21.7450 表4S,,S(G)S(G.,D间的相关分析 Table 4 The Relation Analysis of S().(G).S(C).J.D 相关系数 5(G) S(G) S(G) J 0 1.000000 0.936554 0903123 -0.8g2351 0.992351 S(G) 1.000m 0970536 -0.9137 0.591137 5() 1.0000 -0.97324 0.97332 1.000000 -1.00000 1.000000 表5S(G.S4(G.(G.1D间的偏相关分桥 Table5 The Partial Relation Analysisof)(C).)D 粮相关系数 Sy(G) Su(G) 5G分 D 100000 -0.999303 0.999709 -0036334 0036334 S(G 1.000w -0000196 0.000196 5(G 1.000000 0.02416 -001241 1.00000 -1.0000 1.000000 4结论与讨论 一个具有多态性的非平衡位点,存在着基因水平与基因型水平上的变异,如何客观地测量 变异的程度,是多样性研究与应用的基础. 万方数据
第3期 孛|I满才等非平衡群体基因变异测量的Shannon信息量方法 表3模拟群体的D,曰,亏’(G)分析(续 Table 3 The D,冉、S’(G)Analysis of the Simulation Population{Continues) 表5 sj(G)、雪0(G).童‘(G),正D问的偏相关分析 Table 5 Tile Partial Relation Analysis of sj(G).s;(G),S J(G),J,D 4结论与讨论 一个具有多态性的非平衡位点,存在着基因水平与基因型水平上的变异,如何客观地测量 变异的程度,是多样性研究与应用的基础. 万方数据

346 坐物数华学报 第16卷 1)D与A的差异表明:前人用D作为基因多样度的测承指标是合理的,用开不能测量 非平衡群体的基因变异。 2)D与SG),5(G,Sn(G的强正相关性表明:5(G,S(⑤,SH(G)也可作为度量群体 遗传变异的指标。 D的取值范围为,《一5G)的取值范围为包,川,它们的透传学意 义是相同的,都可描述该位点的基因型不背定性程度。在实际应用时,当群体中某些基因型领 率过小(K0.03)时,由于S"G与S(G)间存在显著差异,因此该群体的S"(C)就成为表征其 基因型变异的恰当尺度 3)由表1模拟结果,J与D的简单相关与偏相关系数均为 简单相关系数为0.93654,而偏相关系数为 sSG)与SG)的 0. 9303,说明J与D,5(G与54(G在 本质上是对应的,但(⑤)与4(G)的简单相关却为正,其原因有待进一步研究。1D与 G).S(G,SG间仅有微弱的偏相关,因而是两个独立的指标体系,且后者还有其信息论 内涵 4)D虽然可作为度量非平衡群体遗传变异的指标,但由于它只利用了基因库资料 有利用基因型的信息因而本质上是用平衡群体作为同一基因库的代表 面没 这种方法本身存在对 信息的损失,反映在用D米度:具有同一基因库的所有群体的基因型变异时,其数值与"(O 比较显著偏小 引S号(G⑨与S(G)可实现对基因型永平上的遗传变异进行刚分.SG反映的是纯合基 因型遗传变异对总变异的贷献,5,(©)反映的是杂合基因型的遗传变异对总变异的贡献。 种副分可为相关遗传现象的解释,透传变异的定向控制,生物多样性 的保持机制及保持方法提 供理论依据。 )对非平衡群体,其遗传变异不可忽视S%(G).即就是说,当杂合体很少时,遗传变异主 般提整时 7)无论是平衡群体还是非平衡群体,基因水平上的变异与基因型水平上的变异都可以用 S(G)来表示. 5实例分析 文献间中用大麦复合杂交组合V第4代的酯德基因座A,B和C(即Es1、Es2、E14) 全热路药脑发好动 表8大爱三个酬米因座基因型须率估测结果 Table The Genotype Prequency Eatimation Result of Fat-Synthase Loci Barly Est4 AA A AAAa AA Aa Aa 0.400064004960 0s650.03800075406504009160.2520 万方数据
生物数学学报 第16卷 1)D与日的差异表明:前人用D作为基因多样度的测量指标是合理的,用疗不能测量 非平衡群体的基因变异. 2)D与s7(G),髟(G),s备(G)的理正相关性表明:雪7(G),已(G).雪各(G)也可作为度量群体 遗传变异的指标. D的取值范围为Io,!吾1,9(G)的取值范围为【o,1],它们的遗传学意 义是相同的,都可描述该位点的基因型不肯定性程度.在实际应用时,当群体中某些基因型频 率过小(≤o 03)时,由于s’(G)与s7(G)间存在显著差异,因此该群体的s’(G)就成为表征其 基因型变异的恰当尺度. 3)由表l模拟结果,J与D的简单相关与偏相关系数均为~l,髟(G)与雪;,(G)的 简单相关系数为o 936654,而偏相关系数为一o 999303,说明,与D,髟(G)与靠(G)在 本质上是对应的,但髟(G)与亏备(G)的简单相关却为正,其原因有待进一步研究. ,,D与 sj(G)翰(G),s’(G)间仅有微弱的偏相关,因而是两个独立的指标体系,且后者还有其信息论 内涵. 4)D虽然可作为度量非平衡群体遗传变异的指标,但由于它只利用了基因库资料,而没 有利用基因型的信息,因而本质上是用平衡群体作为同一基因库的代表.这种方法本身存在对 信息的损失,反映在用D来度量具有同一基因库的所有群体的基因型变异时,其数值与雪,((书 比较显著偏小. j)D(G)与%(G)可实现对基因型水平上的遗传变异进行剖分.彤(G)反映的是纯台基 因型遗传变异对总变异的贡献,s1二(G)反映的是杂合基因型的遗传变异对总变异的贡献.这 种剖分可为相关遗传现象的解释,遗传变异的定向控制,生物多样性的保持机制及保持方法提 供理论依据. 6)对非平衡群体,其遗传变异不可忽视毋(G)即就是说,当杂合体很少时,遗传变异主 要由纯合体引起,用彤(G)或s7(G)度量群体遗传变异都是合适的.对基因型频率适中的群 体(尽管不平衡),s’(G)是度量遗传变异的恰当尺度. 7)无论是平衡群体还是非平衡群体,基因水平上的变异与基因型水平上的变异都可以用 s7(G)来表示. 5实例分析 文献[4】中用大麦复合杂交组合V第4代的酯酶基因座A,口和G(即Estl、Est2、E。L4) 的一些数据证实(we-r等,1972):对于自交物种,基因多样度作为变异性的指标要优于杂合 性.然而,应用相对信息量指标休系,会得出更为清晰的结果. 丧6 大麦三个醅馥基因座基园型频率估测结果 Table 6 The GeⅡ0type F-。quency Es“nlatjon Result of 3 Fht—Syn“1ase Loci Barly 万方数据

第3期 郭清才等,非平衡裤体活因变异测位的Shann9n倍息景方齿 347 表?大麦三个梅蒸因定革因型变异测度计算结果 Table 7 The Genotype Variatiou Meaurement Calculate Result of 3 Fat-Syuthase Loci Barly Est! Est2 Est4 D (G)S(G)S(G) D S'(C)Sa( D s'(G)Sy(G)S(G) 0,840.90560.G454U160m20.1710C,3s750.27450.113304820.76700.56770.19g3 表7表明:三个位点的D与S(G排序一致,说明D与SG在描述基因变异与遗传变异 上是一致的,显然D比相应的Sy(©小,因此用S(G)来描述基因变异度比用D更为清晰.在 描述遗传变异方面,各相对信息量还有它的特别之处,即可实现对基因型水平上变异的剖分。 如E12位点,总遗传变异度为38,78,基中纯合体变异为24.45%,杂合体变异为11.33% 上述三个位点上纯合体频本分别为093G0,0.9619与0.908M,可见纯合体 远大于杂合体频 率,其遗传变异主要是由于纯合体的连续存在所孩,因面表现出S号(G)也远大于S(G),对 这类群体,仅用S(G)来度量遗传变异也是合适的. [爸考文灯 们根并正彩著.王家玉革分千群件湾传学匀造化论M.北京:农业出版杜。3.122123 以郭平种,群体道传学导论京,农业出板社,1393.314-328:362373. [3倒验君国.王身立.透传分析导论BM长沙:湖南科学技术神版社。199.212-217 []W:素.象云弹,王宁,愈表华泽意传学数报分析-群件邀传学高散型数据分析方法北京中国农业出 版社,1996.113134 )志发.清才,宋花德等.柜对5hanm6n倍泉爱与基因变异的盈.后北农亚人学学报,1998,26()30-31 Shannon Entropy Method in Disequilibrium Population Gene Variation Measuremen YUAN Zhi-fa Shanzi Yaxgling 712100 China) Abstract:Basedoostanonnomationtcggotcedtihmnoalieyo son with gene identity J and genc diversity D. owe couconvey gene variatio the)meanly the topothef of popu h the Key words:Dis Shannon information entropy Gene identity 万方数据
万方数据

非平衡群体基因变异测量的Shannon信息量方法 日万数据支款线然 作者单位: 型 刊名: 生物数学学报STIC PK可 英文刊名: JOURNAL OF BIOMATHEMATICS 年卷(期) 2001,16(3) 引用次数: 15次 考文就6) 1.根井正利.王家玉分子群体遗传学与进化论198 2.郭平仲群体造传学导论1993 3.戴君惕.王身立造传分析导论1989 4WeR徐云碧。王志宁.愈志华造传学数据分析-群体造传学离散型数据分析方法1996 5.袁志发.郭满水.宋世德.边宽江周静芋相对Shannon信息量与基因变异的测量[期刊论文]-西北衣业大学学报 1998(④ 相似文款(3条) 遗传群体中的Sh 征群体速传变异的指标行了较系统的研究 信息 卫能 ,论了它南性 2.期刊论文郭满才.来世德周静茎.袁志发,C0an-cai.S0 NG Shi-dc,Z0 U Jing=业,UN2Zi-f色非平衡群体基 因变异Shannon信息量的测量方法-西北农业大学学报200,28(3) 3.学位论文郭满才群体遗传变异的信息学模型研究200 之整 引文(16) 1.MA GuoJi.LIANG LiJing.FAN YanHui.WANG WenJuan.DAI JiaQing.YUAN ZhiFa The entropy characters of point mutation[期f刊论文]-科学通报(英文版)2008(19) 2.马国际,架图。范含样,王文始.戴家庆志发点突变的性质[期刊论文]-科学通报2008(19 3.陈超英一种基于信息理论的距离系数[期刊论文]-生物数学学报2007(0) 4张宏礼,郭满太.王丽波.刘璐.志发表型同型交配群体的Shannonf信息熵和互信息[期刊论文]-中国农学通报 2005(03) 5.杜俊莉孟德尔群体中亲属关系与相似件度量的信息论模型研究[学位论文]硕士2005 6.张宏礼.郭满木.吴晓华,王丽波.刘魔.周静芋哀志发遗传同型交配下一对等位基因群体的Shannon信息培[期刊 论文]-西北农业学报2004(02) 7,张鸿雁,张宏礼于水遗传同型交配与表型同型交配的信息学性质比较[期刊论文]~黑龙江八一农是大学学报 2001(040
非平衡群体基因变异测量的Shannon信息量方法 作者: 郭满才, 宋世德, 周静芋, 袁志发 作者单位: 西北农林科技大学生命科学学院 刊名: 生物数学学报 英文刊名: JOURNAL OF BIOMATHEMATICS 年,卷(期): 2001,16(3) 引用次数: 15次 参考文献(5条) 1.根井正利.王家玉 分子群体遗传学与进化论 1983 2.郭平仲 群体遗传学导论 1993 3.戴君惕.王身立 遗传分析导论 1989 4.WeiR.徐云碧.王志宁.愈志华 遗传学数据分析-群体遗传学离散型数据分析方法 1996 5.袁志发.郭满才.宋世德.边宽江.周静芋 相对Shannon信息量与基因变异的测量[期刊论文]-西北农业大学学报 1998(4) 相似文献(3条) 1.学位论文 郭满才 遗传群体中的Shannon信息量分析及其应用 1998 该文对信息论的形成与现状、信息论在遗传科学上的应用现状进行了综述.对常用的表征群体遗传变异的指标进行了较系统的研究.以Shannon信息量 为基础,建立了相对纯合度信息量S′(A)、相对杂合度信息量S′(A)和相对信息量S′(A)、非平衡群体的基因型信息量SH(G),相对 纯合度基因型信息量SH′(G)、相对杂合度基因型信息量SH′(G),讨论了它们的性质,并赋予遗传学意义.在此基础上,与纯合度J和杂合度H作了 理论比较.通过计算机模拟及利用现有的陕西四个黄牛群体、六个血液蛋白位点的资料,与该指标体系进行了对比研究.最后,研究了交配制度、选择、突 变、迁移等对群体S′(A)、S′(A、S′(A))的影响,并进一步阐明该指标体系的合理性与客观性. 2.期刊论文 郭满才.宋世德.周静芋.袁志发.GUO Man-cai.SONG Shi-de.ZHOU Jing-yu.YUAN Zhi-fa 非平衡群体基 因变异Shannon信息量的测量方法 -西北农业大学学报2000,28(3) 在Shannon信息量的基础上,对非平衡群体建立了群体基因型相对信息量S′(G),纯合体相对信息量S′J(G)和杂合体相对信息量S′H(G)的概念,并赋 予遗传学意义.与基因一致度J和基因多样度D的理论比较表明,二者在数量规律上有很好的一致性,但又是相对独立的指标体系,且相对信息量还有新的内 涵.S′(G)既能表征基因变异,又能反映基因型水平上的遗传变异,S′J(G)主要反映纯合体的遗传变异,S′H(G)主要反映杂合体的遗传变异.各相对信息量 既可反映群体的遗传变异程度,又能比较不同位点间的遗传变异程度. 3.学位论文 郭满才 群体遗传变异的信息学模型研究 2002 系统研究群体遗传学的形成、数学模型、遗传多样性的指标体系、信息论在遗传学中的应用及DNA数据的分析方法,对于动物分广群体遗传变异分析 具有重要意义。但目前建立在统计学基础上的群体遗传学尚未阐述清楚进化过程群体的熵变规律,而且遗传多态性分析的指标体系不够完善,因而必须 用信息论方法科学描述和丰富遗传多样性的指标体系。此外,分子生物技术的介入及核苷酸序列进化的研究都为群体遗传学的深入研究提供了新的途径 ,但关于DNA序列数据的分析方法需要作进一步的研究。本研究主要体现在以下几个方面: (一)关于群体遗传学的信息论模型研究,主要分为三部 分内容:一是群体平衡的Shannon信息熵的性质和群体平衡建立的熵变性质;二是群体遗传多样性测度的研究;三是非平衡群体的基因变异测量 Shannon信息量的方法研究。得到了如下结论: 1、平衡群体的Shannon信息熵最大,群体平衡的过程是熵的增大过程。 引证文献(16条) 1.MA GuoJi.LIANG LiJing.FAN YanHui.WANG WenJuan.DAI JiaQing.YUAN ZhiFa The entropy characters of point mutation[期刊论文]-科学通报(英文版) 2008(19) 2.马国际.梁丽静.范彦辉.王文娟.戴家庆.袁志发 点突变的熵性质[期刊论文]-科学通报 2008(19) 3.陈超英 一种基于信息理论的距离系数[期刊论文]-生物数学学报 2007(04) 4.张宏礼.郭满才.王丽波.刘璐.袁志发 表型同型交配群体的Shannon信息熵和互信息[期刊论文]-中国农学通报 2005(03) 5.杜俊莉 孟德尔群体中亲属关系与相似性度量的信息论模型研究[学位论文]硕士 2005 6.张宏礼.郭满才.吴晓华.王丽波.刘璐.周静芋.袁志发 遗传同型交配下一对等位基因群体的Shannon信息熵[期刊 论文]-西北农业学报 2004(02) 7.张鸿雁.张宏礼.于永 遗传同型交配与表型同型交配的信息学性质比较[期刊论文]-黑龙江八一农垦大学学报 2004(04)

8张宏礼,郭满木.解小栽,杜俊莉刘建军。周静芋、哀志发近亲交配下母了间基因型联合分布的信息痛性质[期刊论 文]-西北农林科技大学学报(自然科学板)2003(03) 9.张宏礼,郭满本解小,刘建军。周静良志发近亲繁殖下一对等位基因群体的楠性质[期刊论文]~西北农林科 技大学学报(白然科学版2003(01) 10.解小,郭满才张宏礼.刘建军。宋世德周静革袁志发两对等位基因群体箱的性质[明刊论文]生物数学学 2003(04) 1山.张宏礼郭满才刘建军.解小莉.杜俊莉,周静芋袁志发遗使同型交配下母子间基因型联合分布的信息熵性质 [期刊论文]-黄牛杂志2003(02) 12.第满才,袁志发,陈宏.歌社民陕西四个黄牛群体遗传变异的Shannonf信息量分析[期刊论文]-黄牛杂志2003(01) 13.张宏礼.郭满才,杜俊莉,刘建军。解小莉,周静芋袁志发复等位基因群体完全自交下母子间基因型联合分布的楠 性质[期刊论文]-黑龙江八一农是大学学报2003(02) 14刘建军。郭满才解小莉.张宏礼周静,志发性连债群体平衡的信息模型研究[期刊论文]西北农林科技大置 学报(自然科学版2002(05) 15郭满才.解小莉刘建军张宏礼宋世德,周静袁志发复等位基因平衡裤体箱的性质[期刊论文]西北农林科 技大学学报(自然科学版)2002(040 16.张宏礼.刘海泉近亲繁殖下复等位基因群体的箱性质[期刊论文]-黑龙江八一农层大学学报2002(040) 本文链接:http:/d.gwanfangdata.c0acn/Periodical_SWSxXb220103013.asp 下载时间:2010年3月5日
8.张宏礼.郭满才.解小莉.杜俊莉.刘建军.周静芋.袁志发 近亲交配下母子间基因型联合分布的信息熵性质[期刊论 文]-西北农林科技大学学报(自然科学版) 2003(03) 9.张宏礼.郭满才.解小莉.刘建军.周静芋.袁志发 近亲繁殖下一对等位基因群体的熵性质[期刊论文]-西北农林科 技大学学报(自然科学版) 2003(01) 10.解小莉.郭满才.张宏礼.刘建军.宋世德.周静芋.袁志发 两对等位基因群体熵的性质[期刊论文]-生物数学学报 2003(04) 11.张宏礼.郭满才.刘建军.解小莉.杜俊莉.周静芋.袁志发 遗传同型交配下母子间基因型联合分布的信息熵性质 [期刊论文]-黄牛杂志 2003(02) 12.郭满才.袁志发.陈宏.耿社民 陕西四个黄牛群体遗传变异的Shannon信息量分析[期刊论文]-黄牛杂志 2003(01) 13.张宏礼.郭满才.杜俊莉.刘建军.解小莉.周静芋.袁志发 复等位基因群体完全自交下母子间基因型联合分布的熵 性质[期刊论文]-黑龙江八一农垦大学学报 2003(02) 14.刘建军.郭满才.解小莉.张宏礼.周静芋.袁志发 性连锁群体平衡的信息模型研究[期刊论文]-西北农林科技大学 学报(自然科学版) 2002(05) 15.郭满才.解小莉.刘建军.张宏礼.宋世德.周静芋.袁志发 复等位基因平衡群体熵的性质[期刊论文]-西北农林科 技大学学报(自然科学版) 2002(04) 16.张宏礼.刘海泉 近亲繁殖下复等位基因群体的熵性质[期刊论文]-黑龙江八一农垦大学学报 2002(04) 本文链接:http://d.g.wanfangdata.com.cn/Periodical_swsxxb200103013.aspx 下载时间:2010年3月5日