
中国农业大学学报2001.6(3):44一49 Journal of China Agricultural University 作物品种区域试验中品种均值的Bayes估计0 张群远②孔繁玲 (中国农业大学作物学院) 摘要本研究根据Bayes统计原理,提出作物品种区域试验中品种均值的Bayes估计方法:并利用一套包 含4年,7个试点和10个棉花品种的多年多点试验对Byes估值和算术平均值的预测精度进行比较。结果表 明,Bayes估值和算术平均值的平均预测差分别为6.88%和12.77%:而且Bays估值与验证值之间在数值 和品种排序上都有着更高的相关,相关系数分别达0.963和0.976,高于算术平均值的0.876和0.830: Bayes估值显示出比算术平均值更高的预测精度。 关键词区域试验,Bay©s估计,算术平均值,预测精度 中图分类号S114 Bayesian Estimation of Variety Means in Regional Crop Trials Zhang Quny pScience Abstract Based on the principle of Bayesian Statistics,a Bayesian method for estimating variety means in regional crop trials was proposed.A trial involving 4 years and 7 sites and 10 varieties of cotton was carried out and analyzed to compare the predictive accuracy of the Bayesian estimates and arithmetic means.It was found that the averaged predictive differences of Bayesian estimates and arithmetic means were 6.88%and 12.77% respectively:the coefficients of correlation between Bayesian estimates and validation data were 0.963 for values and 0.976 for variety ranks,higher than 0.876 and 0.830 of between arithmetic means and validation data.Bayesian estimates showed higher predictive accuracy than arithmetic means. Key words regional trial;Bayesian estimation:arithmetic mean:predictive accuracy 作物品种区域试验(简称区试)是在多环境下对新品种进行比较的规模较大的农业试验。 准确估计各品种在区试中的性状总均值(简称品种均值)是评价品种平均生产性能(譬如丰产 性)的重要依据,因而也是区试中最基本和最重要的统计内容。对于品种均值,区试中习惯于直 接用算术平均值估计。尽管算术平均值满足线性无偏(linear unbiased)、最小二乘(least squares)和极大似然(maximum likelihood)等统计特性,但对于区试品种均值的估计米说,仍 然存在一定局限。从某种意义上讲,算术平均值实质上是对品种试验表现的事后描述,并非对 品种未来表现的预测,而后者是我们真正感兴趣的,具有更重要的实践意义。目前我国区试中, (稿日期:2000- D家自然券基资助项目(30070433) 长群远 京圆明园西路2号中国农业大学(西校区),100094
中国农业大学学报 !""#$%&’()**+*, -./0123.4567128907:/3;/0230?7;@ A 作物品种区域试验中品种均值的 BCDEF估计A 张群远G 孔繁玲 &中国农业大学作物学院( 摘 要 本研究根据 H2@>?统计原理$提出作物品种区域试验中品种均值的 H2@>?估计方法I并利用一套包 含 *年JK个试点和 #"个棉花品种的多年多点试验对 H2@>?估值和算术平均值的预测精度进行比较L结果表 明$H2@>?估值和算术平均值的平均预测差分别为 %MNNO 和 #!MKKOI而且 H2@>?估值与验证值之间在数值 和品种排序上都有着更高的相关$相关系数分别达 "M,%’和 "M,K%$高于算术平均值的 "MNK%和 "MN’"I H2@>?估值显示出比算术平均值更高的预测精度L 关键词 区域试验IH2@>?估计I算术平均值I预测精度 中图分类号 P##* BCDEFQCRSFTQUCTQVRVWXCYQETDZECRFQR[E\QVRC]^YV_‘YQC]F a6219b/1@/21 c.19d213719 &5.33>9>.450.eP:7>1:>$58i.1;6>e071:7e3>.4H2@>?721P;2;7?;7:?$2H2@>?721j>;6.i4.0>?;7j2;719 =207>;@j>21?710>97.123:0.e;0723?k2?e0.e.?>iM8 ;072371=.3=719*@>20?21iK?7;>?21i #"=207>;7>?.4:.;;.1k2?:2007>i./;21i2123@l>i;.:.je20>;6>e0>i7:;7=>2::/02:@.4;6> H2@>?721 >?;7j2;>? 21i 207;6j>;7: j>21?M m;k2? 4./1i ;62;;6> 2=>029>i e0>i7:;7=> i744>0>1:>? .4 H2@>?721 >?;7j2;>? 21i 207;6j>;7: j>21? k>0> %MNNO 21i #!MKKO 0>?e>:;7=>3@I;6>:.>447:7>1;?.4:.00>32;7.1n>;k>>1H2@>?721>?;7j2;>?21i=237i2;7.1i2;2 k>0>"M,%’4.0=23/>?21i"M,K%4.0=207>;@021o?$6796>0;621"MNK%21i"MN’".4n>;k>>1 207;6j>;7:j>21?21i=237i2;7.1i2;2MH2@>?721>?;7j2;>??6.k>i6796>0e0>i7:;7=>2::/02:@ ;621207;6j>;7:j>21?M pEDqVYrF 0>97.123;0723IH2@>?721>?;7j2;7.1I207;6j>;7:j>21Ie0>i7:;7=>2::/02:@ 作物品种区域试验&简称区试(是在多环境下对新品种进行比较的规模较大的农业试验L 准确估计各品种在区试中的性状总均值&简称品种均值(是评价品种平均生产性能&譬如丰产 性(的重要依据$因而也是区试中最基本和最重要的统计内容L对于品种均值$区试中习惯于直 接用 算 术 平 均 值 估 计L尽 管 算 术 平 均 值 满 足 线 性 无 偏 &371>20/1n72?>i(J最 小 二 乘 &3>2?; ?s/20>?(和极大似然&j2t7j/j 37o>376..i(等统计特性$但对于区试品种均值的估计来说$仍 然存在一定局限L从某种意义上讲$算术平均值实质上是对品种试验表现的事后描述$并非对 品种未来表现的预测$而后者是我们真正感兴趣的$具有更重要的实践意义L目前我国区试中$ 收A 稿日期)!"""u#"u#, A国家自然科学基金资助项目&’""K"*’’( G张群远$北京圆明园西路 !号中国农业大学&西校区($#""",* 万方数据

第3期 张群远等:作物品种区域试验中品种均值的Bayes估计 45 同一批品种一般只进行1年的试验,但由于年份间存在气候条件变化,仅根据1年的算术平均 值判断品种(在以后多年中)的应用价值,可靠性并不高。要提高品种评价的可靠性,一方面可 以增加试验的年份数,另一方面可以采用更有效的统计分析方法。相对而言,前者需消耗较多 的资源(占地和人工等):而后者则几乎不增加任何试验费用。基于后一种想法,本研究从农业 试验中应用较少的贝叶斯(Bayes)统计学原理出发,研究区试中品种均值的Bayes估计方法: 并利用相应的多年多点试验对Bayes估值的预测效果进行分析,以期为区试中品种均值的估 计寻求一种在预测精度上优于传统的算术平均值的方法。 1材料与方法 1.1品种均值的Bayes估计的原理和方法 Bayes方法的基本原理是结合已有经验和认识(称为先验信息)和当前试验信息二者来进 行统计推断]。品种区域试验中,同一套品种要在多个地点(甚至多个年份)重复进行试验,尽 管时间上各地点的试验是同时进行的,但逻辑上我们可以认为是一个地点接一个地点依次进 行的。这样,可以应用Bayes统计的原理,把第1个地点的统计结果作为已知的先验信息,而第 2个地点的试验资料作为试验信息,并根据一定的准则(即Bayes定理)1),对先验信息和试 验信息进行综合,得出新的统计结果;然后,再把这一结果作为先验信息,把第3个地点的试验 资料作为试验信息,再得出新的结果…如此循环,直至最后一个地点,便得到最终的Byes 统计结果。 针对区试中品种均值估计这一问题,现假设我们通过第1个地点的1个试验观测值已认 识到某品种均值:服从先验的正态分布N(4.)。按理,:为品种参数,是一个定值,不应该有 方差:但是,这里我们对以的已有认识是不完全确定的,这种不确定性便以方差岳来度量。这 正是Bayes方法有别于一般统计学的一个重要方面;也正因为如此,才有必要进一步进行试验 观测来更好地认识“。在进一步的试验中(即第2个地点的试验),获得该品种的:个重复观测 值,假定它们是来自正态分布总体N(4,)的随机样本,其样本均值为Y2。结合先验分布信息 (即第1个地点的试验结果)和试验信息(即第2个地点的试验结果),根据Bays公式,可推导 出(见附录)品种均值:服从分布N(2,品),其中: =喷+Y: (1) 品=1/品+n/G (2) 此分布称为:的后验分布,即综合先验信息和试验信息所获得的关于:的新认识。随后, 把4~N(,品)作为新的先验分布,进一步试验(即第3个地点的试验),假定有?个重复观 测值来自总体N(4,),算术平均值为Y,再综合二者信息可再次得到μ的后验分布N( ),其中: %-房+小-房4+学,+ (3) (4 万方数据 后=7%+,/G-1/i+,/0+%/网 按此做法,不断进行试验和估计,形成一个迭代的过程。到最后第、个地点的试验,可得到
同一批品种一般只进行 !年的试验"但由于年份间存在气候条件变化"仅根据 !年的算术平均 值判断品种#在以后多年中$的应用价值"可靠性并不高%要提高品种评价的可靠性"一方面可 以增加试验的年份数"另一方面可以采用更有效的统计分析方法%相对而言"前者需消耗较多 的资源#占地和人工等$&而后者则几乎不增加任何试验费用%基于后一种想法"本研究从农业 试验中应用较少的贝叶斯#’()*+$统计学原理出发"研究区试中品种均值的 ’()*+估计方法& 并利用相应的多年多点试验对 ’()*+估值的预测效果进行分析"以期为区试中品种均值的估 计寻求一种在预测精度上优于传统的算术平均值的方法% , 材料与方法 ,-, 品种均值的 ./012估计的原理和方法 ’()*+方法的基本原理是结合已有经验和认识#称为先验信息$和当前试验信息二者来进 行统计推断3!"45 %品种区域试验中"同一套品种要在多个地点#甚至多个年份$重复进行试验"尽 管时间上各地点的试验是同时进行的"但逻辑上我们可以认为是一个地点接一个地点依次进 行的%这样"可以应用 ’()*+统计的原理"把第 !个地点的统计结果作为已知的先验信息"而第 4个地点的试验资料作为试验信息"并根据一定的准则#即 ’()*+定理$3!"45 "对先验信息和试 验信息进行综合"得出新的统计结果&然后"再把这一结果作为先验信息"把第 6个地点的试验 资料作为试验信息"再得出新的结果77如此循环"直至最后一个地点"便得到最终的 ’()*+ 统计结果% 针对区试中品种均值估计这一问题"现假设我们通过第 !个地点的 8!个试验观测值已认 识到某品种均值 9服从先验的正态分布 :#9;!" 9;4? 9;6?作物品种区域试验中品种均值的 ’()*+估计 FH 万方数据

46 中国农业大学学报 2001年 最终的后验分布为N(4,),其中: (5) 1 2= (6) 式中:和Y,分别为第i个地点的试验重复数和品种算术平均值。在2次损失的意义下,依 据后验风险最小的原则,后验均值4,即为品种均值u的Bays估计四。若以地点i的试验误差 方差估计,以第1个地点上试验的品种均值Y,和该均值的误差方差(等于误差方差子除 以重复数1,即/m1)分别估计1和品,则据(5)和(6)式可得到和的估值: (7) 0i= (8) n/s 式中:.即为品种均值的Bayes估值,品为品种均值方差的Bayes估值。 更一般地,若把s个试点,w个品种,r次重复(即所有试点上重复数,=r)的区试中品种 在地点i上的平均值记为Y,品种j的Bayes估值记为B,其方差记为Sm,则: (9) S=- (10) r/si 由此可见,Bayes估值其实是品种在各试点上的多个算术平均值的加权平均值,其权重是 各试点试验误差方差的倒数,而Bayes估值的方差则是各试点品种算术平均值的方差的调和 平均数。 1.2试验资料与设计 为了对品种Bayes估值的实际预测效果进行研究,选择建国以来黄河流域具有代表性的 10个棉花品种,连续进行了4年的多点试验(表1)。各点次均采用随机完全区组设计,3~4次 重复,3行区,小区面积20m?,种植管理和性状考察按目前国家区试标准进行。小区产量转换 为每公顷产量,单位kghm-2。 表1试验资料及与设计 年份 参试点 重复数 参试品种 1996沧州,安阳,西华,临清 岱15,徐州1818,徐州142 1997 沧州,安阳,西华,临清,菏泽 3 1998 沧州,安阳,西华,临清,菏泽,运城,北京 3 中棉所12号,CK(为目前生产用种) 1999沧州,安阳,西华,临清,菏泽,运城,北京 3 中棉所19号,石远321 万方数据
!最终的后验分布为 "#!$%&’ ( $%)&其中* !$%+’ ( $% , ’( $, !$,-. % /+( 0/ ’( / 2 1/ 3 #4) ’ ( $%+ , ,5’( $,-. % /+( 0/5’( / #6) 式中* 0/和 1/分别为第 /个地点的试验重复数和品种算术平均值7在 (次损失的意义下&依 据后验风险最小的原则&后验均值 !$%即为品种均值 !的 89:; 7若以地点 /的试验误差 方差 % ( /估计 ’ ( /&以第 ,个地点上试验的品种均值 1,和该均值的误差方差#等于误差方差 % ( ,除 以重复数 0,&即 % ( ,50,)分别估计 !$,和 ’ ( $,&则据#4)和#6)式可得到 !$%和 ’ ( $%的估值* ! ? $%+’ ?( $%. % /+, 0/ %( / 1/ #@) ’ ?( $%+ , . % /+, 0/5%( / #A) 式中* B ? C<即为品种均值的 89:;<估值&D ?( C<为品种均值方差的 89:;<估值7 更一般地&若把 %个试点&E个品种&F次重复#即所有试点上重复数 0/+F)的区试中品种 G 在地点 /上的平均值记为 1/G&品种 G的 89:;<估值记为 HG&其方差记为 IHG&则* HG+. % /+, , %( / 1/G . % /+, , %( / #J) IHG+ , . % /+, F5%( / #,K) 由此可见&89:;<估值其实是品种在各试点上的多个算术平均值的加权平均值&其权重是 各试点试验误差方差的倒数&而 89:;<估值的方差则是各试点品种算术平均值的方差的调和 平均数7 LMN 试验资料与设计 为了对品种 89:;<估值的实际预测效果进行研究&选择建国以来黄河流域具有代表性的 ,K个棉花品种&连续进行了 O年的多点试验#表 ,)7各点次均采用随机完全区组设计&PQO次 重复&P行区&小区面积 (KR( &种植管理和性状考察按目前国家区试标准进行7小区产量转换 为每公顷产量&单位 STUVRW( 7 表 , 试验资料及与设计 年 份 参 试 点 重 复 数 参 试 品 种 ,JJ6 沧州&安阳&西华&临清 O 岱 ,4&徐州 ,A,A&徐州 ,O( ,JJ@ 沧州&安阳&西华&临清&菏泽 P 鲁棉 ,号&鲁棉 6号&冀棉 A号& 中棉所 ,(号#为种质库原种) ,JJA 沧州&安阳&西华&临清&菏泽&运城&北京 P 中棉所 ,(号&XY#为目前生产用种) ,JJJ 沧州&安阳&西华&临清&菏泽&运城&北京 P 中棉所 ,J号&石远 P(, O6 中 国 农 业 大 学 学 报 (KK,年 万方数据
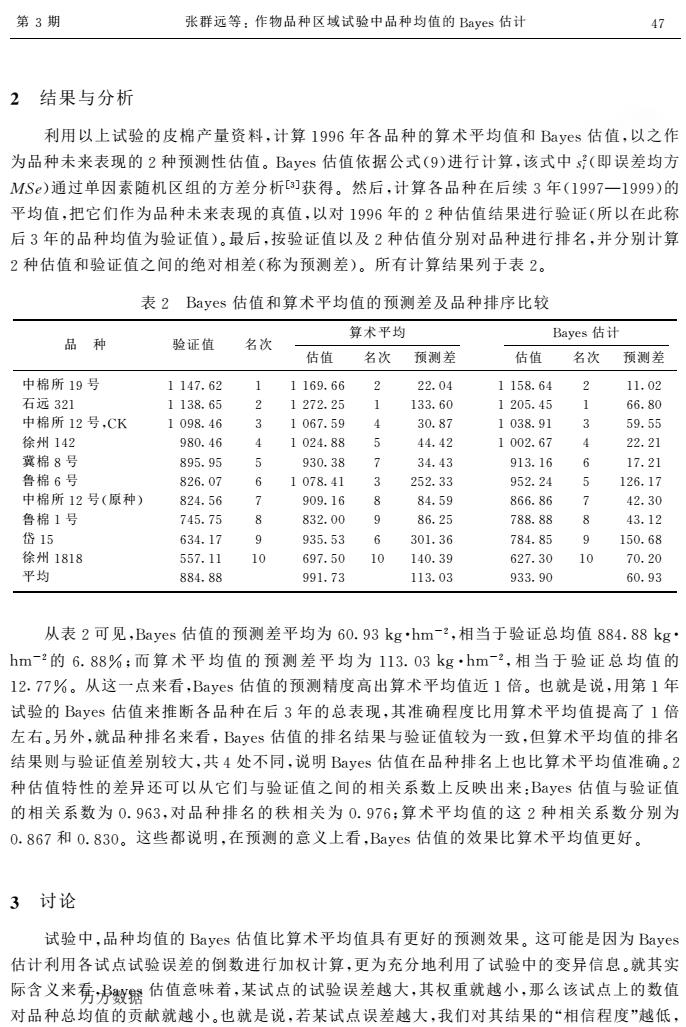
第3期 张群远等:作物品种区域试验中品种均值的Bayes估计 2结果与分析 利用以上试验的皮棉产量资料,计算1996年各品种的算术平均值和Bays估值,以之作 为品种未来表现的2种预测性估值。Bayes估值依据公式(9)进行计算,该式中s(即误差均方 MS)通过单因素随机区组的方差分析]获得。然后,计算各品种在后续3年(1997一1999)的 平均值,把它们作为品种未来表现的真值,以对1996年的2种估值结果进行验证(所以在此称 后3年的品种均值为验证值)。最后,按验证值以及2种估值分别对品种进行排名,并分别计算 2种估值和验证值之间的绝对相差(称为预测差)。所有计算结果列于表2。 表2 Bayes估值和算术平均值的预测差及品种排序比较 算术平均 Baves估计 品种 验证值 名次 估值名次预测差 估值 名次预测差 中棉所19号 1147.62 1169.66 2 22.04 1158.64 2 11.02 右远321 1138.65 2 1272.25 1 133.60 1205.45 1 66.80 中棉所12号,CK 1098.46 1067.59 30.87 1038.91 59.55 徐州142 980.46 1024.88 1002.67 冀棉8号 895.95 930.38 913.16 鲁棉6号 826.07 6 1078.41 252.33 952.24 126.17 中棉所12号(原种) 824.56 2 909.16 8 84.59 866.86 7 42.30 鲁棉1号 745.75 8 832.00 86.25 788.88 R 43.12 代15 634.17 0 935.53 6 36 4.85 8 150. 徐州1818 557.1 10 697.5 140.3 62.30 10 70.20 平均 884.88 991.73 113.03 933.90 60.93 从表2可见,Bayes估值的预测差平均为60.93kghm-2,相当于验证总均值884.88kg hm-的6.88%:而算术平均值的预测差平均为113.03kg·hm-2,相当于验证总均值的 12.77%。从这一点来看,Bayes估值的预测精度高出算术平均值近1倍。也就是说,用第1年 试验的Bayes估值来推断各品种在后3年的总表现,其准确程度比用算术平均值提高了1倍 左右。另外,就品种排名米看,Bayes估值的排名结果与验证值较为一致,但算术平均值的排名 结果则与验证值差别较大,共4处不同,说明Bayes估值在品种排名上也比算术平均值准确。2 种估值特性的差异还可以从它们与验证值之间的相关系数上反映出来:Bayes估值与验证值 的相关系数为0.963,对品种排名的秩相关为0.976:算术平均值的这2种相关系数分别为 0.867和0.830。这些都说明,在预测的意义上看,Bayes估值的效果比算术平均值更好。 3讨论 试验中,品种均值的Bayes估值比算术平均值具有更好的预测效果。这可能是因为Bayes 估计利用各试点试验误差的倒数进行加权计算,更为充分地利用了试验中的变异信息。就其实 际含义米秀乃数继估值意味着,某试点的试验误差越大,其权重就越小,那么该试点上的数值 对品种总均值的贡献就越小。也就是说,若某试点误差越大,我们对其结果的“相信程度”越低
! 结果与分析 利用以上试验的皮棉产量资料"计算 #$$%年各品种的算术平均值和 &’()*估值"以之作 为品种未来表现的 +种预测性估值,&’()*估值依据公式-$.进行计算"该式中 / + 0-即误差均方 123.通过单因素随机区组的方差分析456获得,然后"计算各品种在后续 5年-#$$78#$$$.的 平均值"把它们作为品种未来表现的真值"以对 #$$%年的 +种估值结果进行验证-所以在此称 后 5年的品种均值为验证值.,最后"按验证值以及 +种估值分别对品种进行排名"并分别计算 +种估值和验证值之间的绝对相差-称为预测差.,所有计算结果列于表 +, 表 + &’()*估值和算术平均值的预测差及品种排序比较 品 种 验证值 名次 算术平均 &’()*估计 估值 名次 预测差 估值 名次 预测差 中棉所 #$号 ##97:%+ # ##%$:%% + ++:;9 ##? #;$=:9% 5 #;%7:<$ 9 5;:=7 #;5=:$# 5 <$:<< 徐州 #9+ $=;:9% 9 #;+9:== < 99:9+ #;;+:%7 9 ++:+# 冀棉 =号 =$<:$< < $5;:5= 7 59:95 $#5:#% % #7:+# 鲁棉 %号 =+%:;7 % #;7=:9# 5 +<+:55 $<+:+9 < #+%:#7 中棉所 #+号-原种. =+9:<% 7 $;$:#% = =9:<$ =%%:=% 7 9+:5; 鲁棉 #号 79<:7< = =5+:;; $ =%:+< 7==:== = 95:#+ 岱 #< %59:#7 $ $5<:<5 % 5;#:5% 7=9:=< $ #<;:%= 徐州 #=#= <<7:## #; %$7:<; #; #9;:5$ %+7:5; #; 7;:+; 平均 ==9:== $$#:75 ##5:;5 $55:$; %;:$5 从表 +可见"&’()*估值的预测差平均为 %;:$5@ABCDE+ "相当于验证总均值 ==9:==@AB CDE+的 %:==FG而 算 术 平 均 值 的 预 测 差 平 均 为 ##5:;5@ABCDE+ "相 当 于 验 证 总 均 值 的 #+H77F,从这一点来看"&’()*估值的预测精度高出算术平均值近 #倍,也就是说"用第 #年 试验的 &’()*估值来推断各品种在后 5年的总表现"其准确程度比用算术平均值提高了 #倍 左右,另外"就品种排名来看"&’()*估值的排名结果与验证值较为一致"但算术平均值的排名 结果则与验证值差别较大"共 9处不同"说明 &’()*估值在品种排名上也比算术平均值准确,+ 种估值特性的差异还可以从它们与验证值之间的相关系数上反映出来I&’()*估值与验证值 的相关系数为 ;:$%5"对品种排名的秩相关为 ;:$7%G算术平均值的这 +种相关系数分别为 ;H=%7和 ;:=5;,这些都说明"在预测的意义上看"&’()*估值的效果比算术平均值更好, J 讨论 试验中"品种均值的 &’()*估值比算术平均值具有更好的预测效果,这可能是因为 &’()* 估计利用各试点试验误差的倒数进行加权计算"更为充分地利用了试验中的变异信息,就其实 际含义来看"&’()*估值意味着"某试点的试验误差越大"其权重就越小"那么该试点上的数值 对品种总均值的贡献就越小,也就是说"若某试点误差越大"我们对其结果的K相信程度L越低" 第 5期 张群远等I作物品种区域试验中品种均值的 &’()*估计 97 万方数据

48 中国农业大学学报 2001年 这与我们的一般直觉和经验是吻合的。Byes估计把试验看作连续动态的统计推断,从哲学意 义上讲,也似乎更符合“实践,认识,再实践,再认识”的规律。当然,该方法是否适宜在区试中广 泛应用,或者说适宜在何种作物何种区试中应用,尚需在更多试验和研究来验证和判断。但从 本文可看出,Bayes统计学有其自身得特点,若在农业试验中加以研究利用,有可能使我们得 到一些新的方法和启迪。 另外,从Bayes估值的最终计算公式(9)和(10)来看,Bayes估值与试验地点的在分析中 的先后顺序并无关系,之所以把试验看作各试点依次进行,只是为便于从Bayes统计学的角度 论述问题而已,实际区试的试验方案中无须考虑试点的顺序问题。就计算过程而言,Bayes估 值的计算比算术平均值稍复杂一点,但也很容易实现。并且,由于根据公式(9)和(10)可同时计 算出Bayes估值及其方差,所以,在作实际品种分析时,很容易对各品种的Bayes均值作出区 间估计和差异显著性测验。就此看来,品种的Bayes估值在实际应用中是简单和实用的。 最后要说明的是,关于区试中品种均值的估计,也存在着一些基于混合线性模型(mixed linear model)的方法,如线性无偏预测(best linear unbiased prediction,.BLUP)等~o】。这些方 法通常主要用于处理非平衡数据的问题,计算往往比较复杂,目前作者正在对其作进一步的研 参考文献 中山大学数学力学系.概率论及数理统计,北京:高等教育出版社,1984 2王松贵,线性模型的理论及应用.合肥:安徽教育出版社,1986 3莫惠栋.农业试验统计.(第2版).上海:上海科学技术出版社,1992 4朱军.遗传模型分析方法.北京:中国农业出版社,1997 5 Hill RR I.Rosenberger I l.Methods for combination data from germplasm evaluation trials.Crop Science,1985,25:467~470 6 Peipho H P.Best linear unbiased prediction(BLUP)for regional trials:a comparison to additive main effects and multiplicative interaction(AMMI)analysis.Theor Appl Genet.,1994.89647654 附 已知Bayes公式如下: p(0x)=cp(xl0)·p(0) 试中:p(0)为参数0的先验分布:p(x0)观测值的似然函数;c是与0无关的常量:p(川x) 为结合先验分布(已知信息)和观测值(试验信息)得出的0的后验分布。 现在我们感兴趣的参数为平均值以。假设有n个观测值x1,x2,…,x。为来自正态总体N (红,2)的随机样本,其样本均值为x,则这些观测值的似然函数为: p,l=(2)exp-二)=(2x)iexp- 2a1 2 Jexp(-u(u x 苦令c=克择)exp- x ,6=exp(-行,则有:
这与我们的一般直觉和经验是吻合的!"#$%&估计把试验看作连续动态的统计推断’从哲学意 义上讲’也似乎更符合(实践’认识’再实践’再认识)的规律!当然’该方法是否适宜在区试中广 泛应用’或者说适宜在何种作物何种区试中应用’尚需在更多试验和研究来验证和判断!但从 本文可看出’"#$%&统计学有其自身得特点’若在农业试验中加以研究利用’有可能使我们得 到一些新的方法和启迪! 另外’从 "#$%&估值的最终计算公式*+,和*-.,来看’"#$%&估值与试验地点的在分析中 的先后顺序并无关系’之所以把试验看作各试点依次进行’只是为便于从 "#$%&统计学的角度 论述问题而已’实际区试的试验方案中无须考虑试点的顺序问题!就计算过程而言’"#$%&估 值的计算比算术平均值稍复杂一点’但也很容易实现!并且’由于根据公式*+,和*-.,可同时计 算出 "#$%&估值及其方差’所以’在作实际品种分析时’很容易对各品种的 "#$%&均值作出区 间估计和差异显著性测验!就此看来’品种的 "#$%&估值在实际应用中是简单和实用的! 最后要说明的是’关于区试中品种均值的估计’也存在着一些基于混合线性模型*/01%2 304%#5/62%3,的方法’如线性无偏预测*7%&8304%#59470#&%2:5%20;8064’",等?@ABC !这些方 法通常主要用于处理非平衡数据的问题’计算往往比较复杂’目前作者正在对其作进一步的研 究! 参 考 文 献 - 中山大学数学力学系D概率论及数理统计D北京E高等教育出版社’-+F@ G 王松贵D线性模型的理论及应用D合肥E安徽教育出版社’-+FB H 莫惠栋D农业试验统计 I*第 G版,D上海E上海科学技术出版社’-++G @ 朱军D遗传模型分析方法D北京E中国农业出版社’-++J K L033M M N’M6&%47%5O%5N%0:Q6L >D"%&8304%#59470#&%2:5%20;8064*",R655%O064#3850#3&E#;6/:#50&6486#22080S%/#04 %RR%;8*/9380:30;#80S%048%5#;8064*VPPW,#4#3$&0&DXQ%65V::3Y%4%8D’-++@’F+EB@JABK@ 附 录 已知 "#$%&公式?GC如下E Z*[\]^,_‘aZ*]^\[,bZ*[, 试中EZ*[,为参数 [的先验分布cZ*]^\[,观测值的似然函数c‘是与 [无关的常量cZ*[\]^, 为结合先验分布*已知信息,和观测值*试验信息,得出的 [的后验分布! 现在我们感兴趣的参数为平均值 d!假设有 e个观测值 ]-’]G’f’]e为来自正态总体 g *d’h G ,的随机样本’其样本均值为 ]’则这些观测值的似然函数为E Z*]^\d,_i e ^_- *Gjh G ,k - G%1:lk*]^kd,G GhG m_*Gjh G ,k e G%1:lkn]G ^ GhG m%1:lke*dG kGd], GhG m 若令 ‘-_*Gjh G ,k e G,%1:lkn]G ^ GhG m’‘G_%1:lke]G GhGm’则有E @F 中 国 农 业 大 学 学 报 G..-年 万方数据

第3期 张群远等:作物品种区域试验中品种均值的Bayes估计 49 cp(xl)=Gexp(-nr二2) 202 另外,已知4具有先验分布N(4,),即: p(四=(2xai)-xp-- 26 令c3=(2π)支,则有: Gxp-Gep-号(停+品+(学+完+(器+亮 再令0-(学+品,k-i学+完.=6p器+编-(2xp(一编.则有: (p()(2)-texp-) C: 202 令c=(c2c5)/(c1c3),因为c为常量,且与r无关,所以最后得到r的后验分布为: p(nz)=c·p(ax)·p)=(2xi)texp--4) 20 由此可见,μ服从后验的正态分布N(4,)。在此,只需用%1,听,,,后,2和Yz分别 代替以上的o,品,2,4,,n和x,文中(1)和(2)式即可得证。 万方数据
!"#$%&’()*!+,-./01$%0() "2" 3 另外4已知 (具有先验分布 5$(642 " 6)4即7 #$()*$"82 " 6)0 + ",-./0$(0(6)" "2" 6 3 令 !9*$"82 " 6)0 + "4则有7 !"#$(’%&)#$()*!+!9,-./0(" "$1 2": + 2" 6 ):$ 1% 2":(6 2" 6 )(:$ 1%" "2": (" 6 "2" 6 )3 再令 + 2" ; *$1 2": + 2" 6 )4(;*2 " +$ 1% 2":(6 2" 6 )4!$!+!9!<)4因为 !为常量4且与 (无关4所以最后得到 (的后验分布为7 #$(’%&)*!?#$(’%&)?#$()*$"82 " +)0 + ",-./0$(0(;)" "2" ; 3 由此可见4(服从后验的正态分布 @$(;42 " ;)A在此4只需用 (;+42 " ;+42 " "4(;"42 " ;"41"和B"分别 代替以上的 (642 " 642 " 4(;42 " ;41和 %4文中$+)和$")式即可得证A 第 9期 张群远等7作物品种区域试验中品种均值的 DEF,G估计 <C 万方数据

作物品种区域试验中品种均值的Bayes估计 日万方意据支秋铁热 作者: 张群远,孔繁玲 作者单位: 中国衣业大学作物学院 刊名: 中国农业大学学报STCP可 英文刊名: JOURNAL OF CHINA AGRICULTURAL UNIVERSITY 年,卷(期): 2001,6(3) 引用次数: 0次 考文然(6条) 1.中山大学数学力学系概率论及数理统计1984 2.王松贵线性模型的理论及应用1986 3.莫惠栋农业试验统计.(第2胞1992 4朱军遗传模型分析方法1997 5.Hill RR J.Rosenberger J L Methods for combination data from germplasm evaluation trials 1985 6.Peipho HP Best linear unbiased prediction(BLUP)for regional trials:a comparison to additive main effects and multiplicative interaction(AMMI)analysis 1994 相似文然(0条) 本文链接:htp:/.anfangdata./Periodical201I03009.a5 下载时间:2010年3月5日
作物品种区域试验中品种均值的Bayes估计 作者: 张群远, 孔繁玲 作者单位: 中国农业大学作物学院 刊名: 中国农业大学学报 英文刊名: JOURNAL OF CHINA AGRICULTURAL UNIVERSITY 年,卷(期): 2001,6(3) 引用次数: 0次 参考文献(6条) 1.中山大学数学力学系 概率论及数理统计 1984 2.王松贵 线性模型的理论及应用 1986 3.莫惠栋 农业试验统计.(第2版) 1992 4.朱军 遗传模型分析方法 1997 5.Hill R R J.Rosenberger J L Methods for combination data from germplasm evaluation trials 1985 6.Peipho H P Best linear unbiased prediction(BLUP) for regional trials: a comparison to additive main effects and multiplicative interaction(AMMI) analysis 1994 相似文献(0条) 本文链接:http://d.g.wanfangdata.com.cn/Periodical_zgnydxxb200103009.aspx 下载时间:2010年3月5日