
4H章元明等:Logistic模型配合家禽生长资料参数ir方法… 第3期 Logistic模型配合家禽生长资料 参数估计方法比较的Monte Carlo研究 章元明焦敏荀平张水祥唐锡政 (四川富牧兽医学院动物科学亲) 摘要本文用Logistic模型配合Monte C,rio方法模拟的30个家禽生长资料,以比较Logis- tc模型参数估计的最小一乘法、摄小二乘法和mnx法,以及线性化方法。结果表明:最小二乘 法(LS》和最小一系法结果相当,均优于ix力法参数估计的线性化方法结果较差,以改良三 点法效果较好。 关健词Monte Cario模拟非线性模型均匀设计参数估计 家禽生长资料是数量级悬殊的数据资料,一般用生长模型,如Logistie模型等来配合,其 参数估计方法有:线性化方法,LS法即Marquardt和Gauss-一Newton法等,以及杨运清等 (1993)认为LS法拟合数量级悬殊资料效果不好而提出的mix2方法,然而,章元明(1994 认为mix方法尚有待于进一步研究,为此,本文利用非线性模型参数估计的均匀设计 法,对此进行Monte Carlo模拟研究。另外,农牧基层工作者常采用线性化方法估计模型参 数,而不同方法其结果差别较大,为此,用Monte Carlo方法比较线性化参数估计方法,为应用 者选用方法时提供参考依据。 1研究方法 1.1家腐生长资料数据集的模拟四 本研究用Y=K/(1+-)十e来模拟数据集,共摸拟30个数据集,其中,K=1900,a=3. 6,b=0.1,e一N(0,202),t分别为0,7,14,21,28,35,42,49,56,63.e通过改良混同余法产生, 混同余法产生伪随机数的公式为X+1=mod(aX。+C,m),其中,A=1366,n=714025,C 150889,所产生的伪随机数序列通过了参数检验,独立性检验,均匀性检验,通过函数变换为正 态随机变量后,其结果服从正态分布 1.2统计方法 .2.1 Logistic模型的参数估计方法 1.21.1 Logistic模型参数估计的均匀设计法 具体方法参见文献,通过改变目标函 ·收精日期:1995一09一23 194-010 China Academic Journal Electronic Publishing House.All rights reserved.hitp:/ww
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 章元 明等 “ 模型配 合家 禽生长资料参数 袱 计方法 … … 第 期 模型配合家禽生 长资料 参数估计方法 比较的 兔 研 究 章元明 焦 敏 苟 平 张永祥 唐锡政 四 川 畜牡 兽医 学院动物科 学 系 摘 要 本文用 模型配 合 忆 二 方法模拟的 个家禽生长资料 , 以 比较 模型参数估计的最小一乘法 、 最 小二乘法和 而 尹 法 , 以及线性化方法 。 结果表明 最小二乘 法 和最 小一乘法结果相当 , 均优于 尹 力 法 参数估计的线性化方法结果较差 , 以改 良三 点法效果较好 。 关健词 模拟 非线性模型 均匀设计 参数估计 家禽生长资料是数量级悬殊 的数据资料 , 一般用生长模型 , 如 。 模型等来配 合 。 其 参数估计方法 有 线性 化方法 , 法 即 和 一 法 等 , 以 及 杨运 清等 认为 法拟 合数量级悬殊 资料效果不好而提 出的 方法团 然而 , 章元 明 认 为 扩 方 法 尚有 待 于 进 一步 研 究闯 , 为此 , 本 文 利 用 非线性 模型 参数 估计 的均 匀 设 计 法 , 对此进行 模拟研究 。 另外 , 农牧基层工作者常采用线性化方法估计模型参 数 , 而不同方法其结果差别较大 , 为此 , 用 方法 比较线性化参数估 计方法 , 为应 用 者选 用方法 时提供参考依据 。 研究方法 家禽生长资料数据集的模拟 本研究用 一 ‘ 来模拟数据集 , 共模拟 个数据集 。 其中 , 一 , 一 , 一 , 。 , , 分别为 。, , , , , , , , , 。 鸟 通过改 良混 同余法产生 , 混 同余法 产生 伪随机 数 的公 式 为 , 一 以 。 , , 其中 , 沃 , , , 所产生的 伪随机数序列通过 了参数检验 , 独立性检验 , 均匀性检验 , 通过 函数变换为正 态随机变量后 , 其结果服从正态分布 。 。 统计方法 模 型 的参数估计方 法 模型 参数估计的均 匀设 计法 具 体方 法参见文 献 , 通 过改变 目标 函 收稿 日期 一 一

1995,9(3) 四川畜牧兽医学院学报 45 数甲目标系数分别为¥-Y.含(Y-X(X-X以面得到参数的最小一 乘和最小二乘和minx的估计值 1.2.1.2 Logistic模型参数估计的三点法假定t,呈等差数列,公差为△(下同),若22= t+t,K=[2YY,Y,-Y(Y,+Y)]/(Y,Y,-Y).然后,利用1n[(K-Y)/N]=a-bt估计参 数a和b。这里,在缓慢增长前期,迅速增长期和后期各取一点以估计参数K. l.2.1.3 Logistic模型参数估计的取N,估K法若Y,<Y+1,且t呈等差数列,则由 In(Y-Y)=In[e'(1-e-)/k]-b 估计出b和e/k。然后,利用曲线通过(t.,Y)(yn为最大Y,值),即Y=K-+(e/K)e, 求出K值。最后,将K值代入e/k中得a值。 1.2.1.4 Logistic模型参数估计的一阶差商法,参考文献o). 1.2.1.5 Logistic揽型参数估计的差分法。利用Y,/Y+1=ebn+[(1-ebo)/K]y,估计出 e一△和(1一e一b△)k,进而得到到b与K,参数a的计算参老文献[)。 1.么.2多元方差分析模型参数为试验指标,参数估计方法为组间差异,进行多元方差分析。 1.2.3平均差和扣对误差平均差及相对误差分别为 An0-24-9 =130 RE()=∑”10-1/8 30 其中,为第i个数据集的参数估计值。 2结果与分析 2.1 Logistic模型参数估计最小一乘,最小二乘和最小×'法比较的Monte Carlo研究 2.1.1参数估计值的多元方差分析经多元方差分析,A=0.102454,从而F=59.48·,即 不同估计方法的参数估计值有极显著差异。由此,可初步认为,LS、最小一乘和mi×2法的参 数估计值之间存在极显著差异 2.1.2LS,最小一乘和minx2法季数估计值的比较 表1 Logistic模型的参数估计结果 参数估计方法一 A·D x s X 5米3.5a74490.083580.0295530.0032715 1905.394228284712641.89133.2178815.46 小-法35834930,10330 0.0996240.0037834 1903.20131.278923106.84124.324816.83 72360.12017 1910.66 44.845823524.1 155090212.658 取Nn告K楼356326 一阶楚商法51257821.998 .15067 0.0633289 1628.357147.083 发分楼3.5809330.31564 0.0997070.0015900 1917.830116.5966 三点传36373490.158360.0083400059303 105.C0539.85145 1994-2010 China Academic Journal Electronic Publishing House.All rights reserved.hip://www.cnki.net
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net , 四 川畜 牧兽 医学 院学报 一 , 一 ‘ ‘ , ,‘ , ‘ 一 一一 一 一一 一 一 一 一 数 , 即 目标 函数分别 为 乙 一 丫 乘和最小二乘和 护 的估计值 。 乙 , 一 , , 乙 、一 ‘ 丫丫 , 从而 得到 参数 的最 小一 。 模型参数 估计的三 点法 假定 呈等差数列 , 公差 为△ 下同 , 若 , , , 一 鑫 , 〕 , 一 婆 。 然后 , 利 用 一 〕一 一 估计参 数 和 。 这里 , 在缓慢增长前期 , 迅速增 长期和 后期各取一点以 估计参数 。 模型参数估计 的取 。 估 法 若 丫 丫十 , , 且 呈等差数列 , 则 由 厂‘ 一 动 一 一 △ 〕一 估计出 和 。 然后 , 利 用曲线通过 。 , 。 为最大 , 值 , 即 哥’ 一 ’ , 一‘, , 求出 值 。 最后 , 将 值代入 叮 中得到 值 。 。 模型参数估计的一 阶差商法 , 参考文献 。 模型参数估计 的差分法 。 利 用 。 , 一 一“ △ 一卜〔 一 一“ △ 玉 , 估计出 一 她和 一 一 她 , 进而得到 与 , 参数 的计算参考文献 。 乞 多元 方差 分析 模型参数为试验指标 , 参数估计方法为组 间差异 , 进行多元方差分析 。 平 均差和 相 对误差 平均差及相对 误差分别 为 · · 一 一 艺泄 其中 , 良为第 个数据集的参数 估计值 。 又 ‘ 世二旦 二下 良一。 结果与分析 模型参数估计最小一乘 、 最小二乘和最小 扩 法比较的 研究 参 数枯 计 值 的 多元 方 差分 析 经多元方差分析 , 一 , 从而 ” , 即 不同估计方法的参数估计值有极 显著差异 。 由此 , 可初步认为 , 、 最小一乘和 扩 法 的参 数估计值之 间存在极显著差异 。 , 最 小 一乘和 扩 法参数枯 计值 的比较 表 模型的参数估计结果 参数估计方法一一 ——— 一 ——— · 妒 又 父 】石 法 , , 最小一乘法 而 毛 取 估 法 一阶差商法 里 差 分 法 了 · 三 点 法 咤
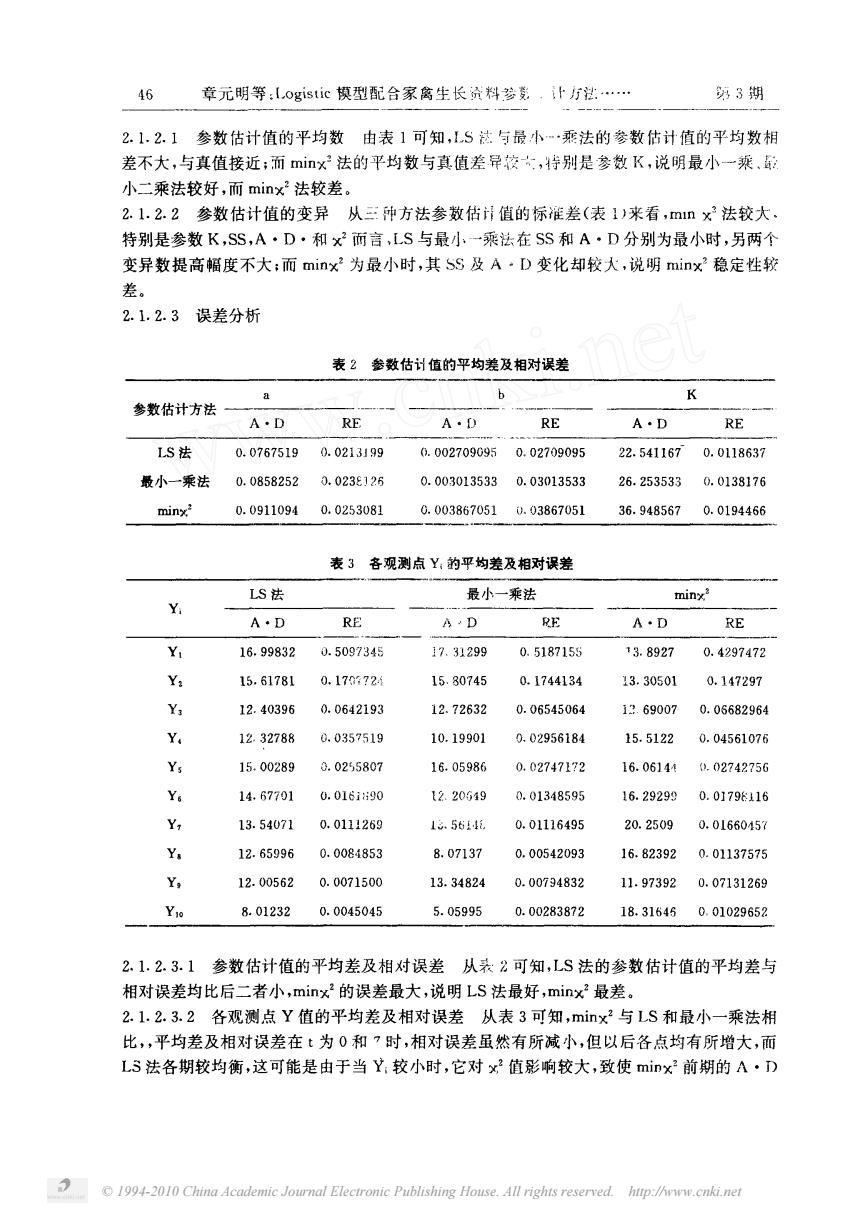
46章元明等:【ogistic模型配合家篱生长资料多莞,让坊法… %3期 2.1.2.1参数估计值的平均数由表】可知,【S达与最小-…乘法的参数估计值的平均数相 差不大,与真值接近:而mix法的平均数与真值差异按之,特别是参数K,说明最小一衰, 小二乘法较好,而minx2法较差。 2.1.2.2参数估计值的变异从三方法参数估值的标准差(表1)来看,mnx法较大 特别是参数K,SS,A·D·和×2而言,【S与最小一乘法在SS和A·D分别为最小时,另两个 变异数提高幅度不大:而minx2为最小时,其SS及A·D变化却较大,说明minx2稳定性较 差。 2.1.2.3误差分析 表2参数估计值的平均差及相对误差 a b K 参数估计方法 A·D RE A·D RE A·D RE S法 0.07675190.0213199 002709095 0.02709095 22.541167 0.0118637 服小一乘法 0.08582520.023E125 0.0030135330.03013533 26.2535330.0138176 minx 0.09110940.0253081 0.003867051.03867051 36.9485670.0194466 表3各观测点Y,的平均差及相对误差 LS法 最小一乘法 minx? A·D RE A·D RE A·D RE 16.9983 0.5097345 17.31299 0.5187155 13.8927 0.4297472 Y 15.61781 0.17072 15.80745 0.1744134 13.30501 0.147297 12.40396 0.0642193 12.72632 0.06545064 13.69007 0.05682964 12.32788 0.0357519 10.19901 0.02956184 15.5122 0.04561076 15.00289 0.025580 16.05986 0.02747172 16.06144 L.02742750 14.67791 0.016i 2.20649 .01348595 16.29299 0.0179116 13.54071 0.011269 l.561 0.01116495 20.2509 0.01660457 Yi 12.65996 0.0081853 8.07137 0.00542093 16.82392 0.01137575 Yx 12.00562 0.0071500 13.34824 0.00734832 11.973920.07131269 801232 0.0045045 5.05995 Q.00283872 18.316450.01029652 2.1.2.3.1参数估计值的平均差及相对误差从表:2可知,LS法的参数估计值的平均差与 相对误差均比后二者小,minx2的误差最大,说明LS法最好,minx2最差。 2.1.2.3.2各观测点Y值的平均差及相对误差从表3可知,minx2与LS和最小一乘法相 比,平均差及相对误差在:为0和?时,相对误差虽然有所减小,但以后各点均有所增大,而 L3法各期较均衡,这可能是由于当Y,较小时,它对×2值影响较大,致使mix前期的A·D 194-2010 China Academic Joual Electronic Publishing House.All rights reserved.hitp://ww
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 章元 明等 才。 让 模 型配 合家 禽生 长 贷 料参 瓷 汁 方祛 · · … 势 期 参数 估计值的平均 数 由表 可知 , 万 摧 与最 小一乘法 的参数 估计值的平 均 数相 差不大 , 与真值接近 而 扩 法 的平均 数与真值差 异较大 , 待别是 参数 , 说 明最小一 乘 、 影 小二乘法较好 , 而 扩 法较差 。 参数估计值的变异 从三 仲方法参数 估计值 的标准差 表 来看 , 厂 法 较大 , 特别是参数 , , · · 和 厂 而 言 , 与最小 一 乘法在 和 · 分别为最小时 , 另两个 变异数提高 幅度 不大 而 才 为最 小 时 , 其 及 · 变化 却较大 , 说 明 才 稳定性较 差 。 误差分析 表 参数估计值的平均差及相对误差 参数估计方法 · · · 法 最小一乘法 。 。 表 各观测点 、 的平均差及相对误差 法 最小一乘法 筑 · 、 八 、 八 · 王 。 飞 , ‘ 今 介 , 二竺 。 。 。 、 。 噢 〔》 。 , 宝牙言 舀 主邃乙 唯 了 , , 参数估计值的平均差及相对 误差 从表 名 可知 , 法 的参数估计值的平均差 与 相对误差均 比后二者小 , 扩 的误差最大 , 说明 法最好 , 扩 最差 。 各观测点 值的平均差及相对误差 从表 可知 , 扩 与 和最小一乘法相 比 , , 平均差及相对误差在 为 。 和 ’ 法各期较均衡 , 这可能是 由于 当 艺 时 , 相对误差虽 然有所减 小 , 但 以后各点均有所增大 , 而 较小时 , 它对 尹 值影 响较大 , 致使 才 前期 的 ·
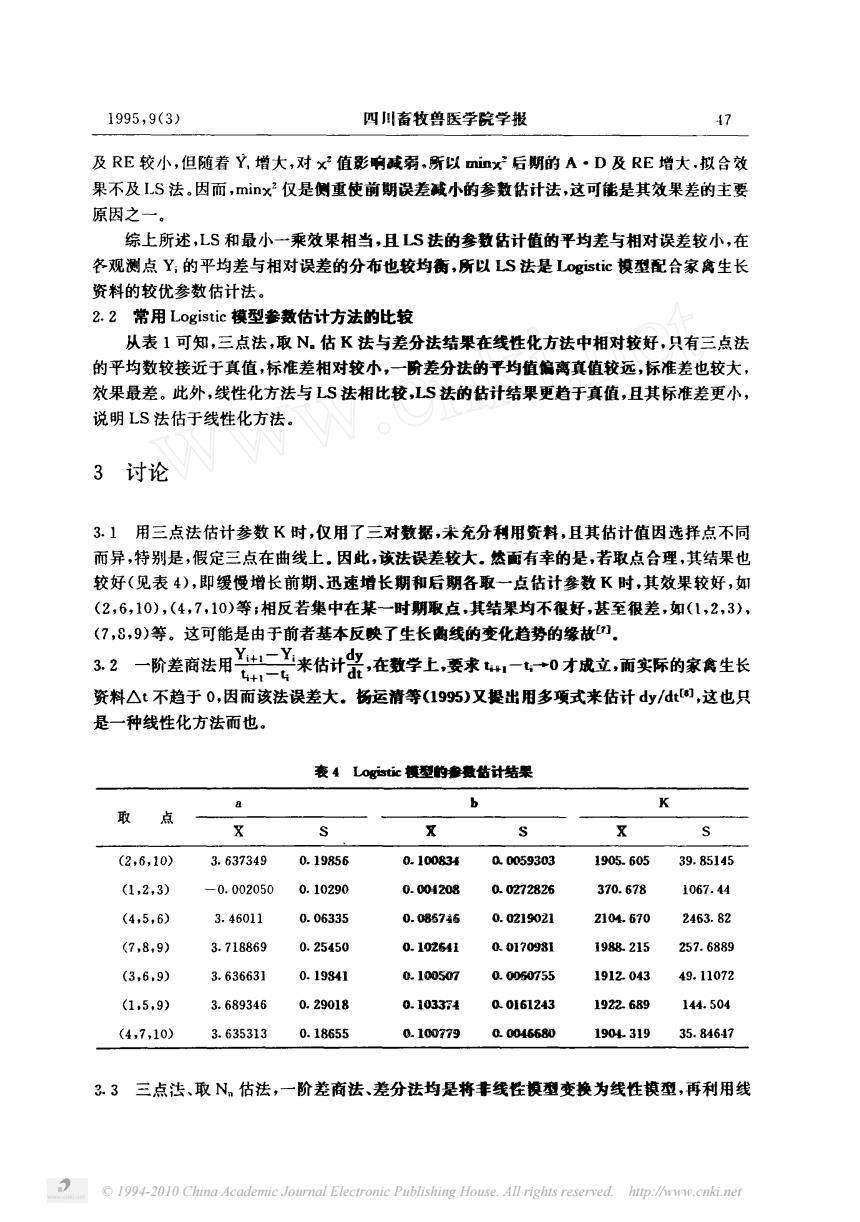
1995,9(3) 四川畜牧兽医学院学报 及RE较小,但随着Y,增大,对×值影响或弱,所以mnx后期的A·D及RE增大,拟合效 果不及S法.因而,mix仅是侧重使前期误差减小的参数估计法,这可储是其效果差的主要 原因之一。 综上所述,LS和最小一乘效果相当,且LS法的参数估计值的平均差与相对误差较小,在 各观测点Y,的平均差与相对误差的分布也较均衡,所以LS法是L©gistic模型配合家禽生长 资料的较优叁数估计法 2.2常用Logistic模型参数估计方法的此较 从表1可知,三点法,取N。估K法与差分法结果在线性化方法中相对较好,只有三点法 的平均数较接近于真值,标准差相对较小,一阶差分法的平均值偏离真值较远,标准差也较大。 效果最差。此外,线性化方法与LS法相比较,LS法的估计结果更趋于真值,且其标准差更小, 说明LS法估于线性化方法。 3讨论 3.】用三点法估计参数K时,仅用了三对数据,未充分利用资料,且其估计值因选择点不同 而异,特别是,假定三点在曲线上.因此,该法误差较大.然面有幸的是,若取点合理,其结果也 较好(见表4),即缓慢增长前期、迅速增长期和后期各取一点估计参数K时,其效果较好,如 (2,6,10),(4,7,10)等:相反若集中在某一时期取点,其结果均不很好,甚至很差,如(1,2,3), (7,8,9)等。这可能是由于前者基本反映了生长幽线的变化趋势的缘故)。 32一阶差商法用二。米估计,在数学上,委求1一七0才成立,而实际的家禽生长 资料△t不趋于0,因而该法误差大。杨运清等(1995)又提出用多项式来估计dy/dt),这也只 是一种线性化方法而也。 表4 Logistic型的参估计结果 取点 b K s (2,6,10) 3.637349 0.19856 0.100834 0.0059303 1905.605 39.85145 (1,2,3) -0.002050 0.10290 0.004208 Q.0272826 370.678 1067.44 (4,5,6) 3.46011 0.0633 0.08574 0.021902 2104.670 2463.82 (7,8,9) 3.718869 0.2545 Q.102641 0.017093 1988.215 257.6889 (3.6,.9) 3.636631 0.19841 0.100507 0.000755 1912.04349.11072 (15,9) 3.689346 0.29018 0.103374 Q.0161243 1922.689 144.504 (4,7,10) 3.635313 0.18655 Q.100779 Q.0046680 1904.319 35.84647 3.3三点法、取N估法,一阶差商法、差分法均是将丰线性模型变换为线性模型,再利用线 1994-2010 China Academie Journal Electronic Publishing House.All rights reserved hup://www.cnki.net
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net , 四 川畜牧兽医学院学报 及 较小 , 但 随着 丫 增大 , 对 尹 值影响减弱 , 所以 加艾竺 后期的 · 及 增 大 , 拟 合效 果不及 法 。 因而 , 扩 仅是侧重使前期误差减小的参数 佑计法 , 这可能是其效果差的主要 原因之 一 。 综上所述 , 和最小一乘效果相当 , 且 另 法的参数估计值的平均差与相对误差较小 , 在 各观测点 、 的平均差与相对误差的分布也较均衡 , 所以 法是 嗯 模型配 合家 禽生长 资料的较优参数估计法 。 常用 模型参数估计方法的比较 从表 可知 , 三点法 , 取 。 估 法与差分法结果在线性化方法 中相对较好 , 只有三点法 的平均数较接近于真值 , 标准差相对较小 , 一阶差分法的平均值偏离真值较远 , 标准差也较大 , 效果最差 。 此外 , 线性化方法与 法相 比较 , 另 法的估计结果更趋于真值 , 且其标准差更小 , 说明 法估于线性化方法 。 讨论 用三 点法估计参数 时 , 仅用了三对数据 , 未充分利 用资料 , 且其估计值因选择点不 同 而异 , 特别是 , 假定三点在 曲线上 。 因此 , 该法误差较大 。 然面有幸的是 , 若取点 合理 , 其结果也 较好 见表 , 即缓慢增 长前期 、 迅速增 长期和后期各取一点 估计参数 时 , 其效果较好 , 如 , , , , , 等 相反若集 中在某一时期取点 , 其结果均不很好 , 甚至很差 , 如 , , , , , 等 。 这可能是由于前者基本反映了生长曲线的变化趋势的缘故川 。 , 、 。 一 丫 ‘ 、 勿 、 ‘ 二 。 小 二、 , ‘ “ 。 一阶差商法用弓创‘ 宁来估计赞 , 在数学上 , 要求 协一‘ 才成立 , ’‘ ’ 面实际的家禽生长 一 ’一 ”一 ’ ” 仁 一叭 ‘ ’ 一 ’ ” ‘ 一一 ’ 一 ’ 一 一 ’ 一 “ “ ’ 一 ’ 一 ’ — 一 ’ 一” 一‘ 一 一 资料△ 不趋于 。 , 因而该法误差大 。 杨运清等 肠 又提出用多项式来估计 , 这也只 是一种线性化方法而也 。 表 叩沁血 祖型的今教佑计结果 卜 取 点 — — — 又 , , 民灿 氏 侧巧, 。 , , 一 让 盛 名 让 。 , , 。 。 召石 谧 狂 , 舰 。 , , 。 标翻 众 名 。 , , 玲 众 你时沁, , 。 , , 炭炸 让 么 , , , , 众 侧匆习以沁 砚 。 三点法 、 取 。 估法 , 一 阶差商法 、 差分法均是将非线性模型变换为线性模型 , 再利 用线

18 章元明等:ogistic模型配合家腐生长筑料参数估计方法… 第3期 性关系估计模型参数或其参数的函数,所得到的估计使仅为特定的线性摸彩的【S估计值,而 不是【ogsc模型的S估计值,从表1可知,线性化方法计模型参数的军不是很好的 3.1畅运清等提出miX法是为了提高非线性模型拟合数量级悬殊资料的梦度”.使其各点 的误差分布均匀)。从表2可知,minY'法的参数估计值误差较大,且误差分有并不妇LS法均 匀,它只不过是为了减少为数较小各点的误差,因而并不如【S法.应当指:.对于数量级悬殊 资料,lS法不如刀切(jackknfe).法,其结果将另文报道。 在使用1S法时,可以采用试验设计法估计棋型参数,若还觉得效更不好,可将其结果 作为Marquardt法的初值,其结果将更佳, 考文材 1洪再吉等译,Ratkowsky,D.A.著.非线性回归模型.南京大学出版社,l986 2徐钟济编著.蒙特卡罗方法。上海科技出版社,1935 3杨运清等,畜牧兽医学报,1992,(2):219-224 4扬运清等.提高非线性模型拟今结果可靠性的一种方法一“×值Marquardt法”,1993,8(3):150一155 生物学学报.9(4).18--1发8 意元男均匀设对在生结连氨型数结计6应用:中国农业科技出版社小9%,70一四 元明.动物生长模型参数初值的探讨中国农业科技出饭社,1995,272一275 8杨运请,刘中源·家畜生态,1995,16(2):14-17 9Gai Juny and Zhang Yuaming.A study of Suitable sample sie in the conservation of landruce on bean.Soybean Genetics Newsletter.May.1993:2730 A MONTE CARLO STUDY ON THE COMPARISON OF PARAMETER ESTIMATION METHODS OF LOGLSTIC MODEL FOR FITTING POULTRY GROWTH DATA Zhang Yuanming Jiao Min et al. Abstract In the paper,Logistic model was used to fit 30 poultry growth data se simulated by Monte Carlo method in order to compare its parameter estimation methods.The results were as follows the resultsof both LS and least absolute deviations methods were proximative,both of them were better than that of min x'method;the results of the lineared methods were relatively poor,but that of the improved three points method were relatively better. Key words Monte Carlo Simulation,Nonlinear Model,Uniform Design,Parameter Esti- mation 14-01 China Academic Jol Electronic Publishing House.All righs reserved.hmp:/.nne
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 墉 章元明等 , 模型配 合家 禽生长 资料参数 沾计方 法 … … 第 期 性关系估计 模型参数或其参数的 函 数 , 所得到的 估计 值仅为特 定的 线性 模飞褚勺 沽 卜放 , 而 不是 模型的 沽计值 , 从表 可知 , 线性化方法 片计模型 参数的杜 军不 是很好的 杨运清等提 出 法是为了提高非线性模型拟 合数量级悬殊 资 料的 件率 ‘ ’ · 使其各 点 的误差分布均 匀闭 。 从表 可知 , 。 厂 法的参数估计值误差较大 , 且 涅差分布并不妇 一 法均 匀 , 它 只不过是为了减少为数较 小各点的误差 , 因而 并不如 法 应当指 , 红’ 一 付于 数量级悬殊 资料 , 另 法不 如刀切 法 , 其结果将另文报道 。 在使用 另 法时 , 可以 采用试验设 计法汇卜司 估计模型 参数 , 若还觉 得效里不好 , 可将其结果 作为 二 , 法的初值 , 其结果将更佳 。 参考文献 洪再吉等译 , , , , 著 非线性回归模型 南京大学 出版社 , 徐钟济编著 蒙特卡罗方法 , 上海科技出版社 , 杨运清等 畜牧兽医学报 , , ”一 杨运清等 · 提高非线性棋型拟 合结果可靠性的一种方法一 “ 值 法 ” , , 一 章元明 , 生物数学学报 , 一 章元明 , 均匀设计在非线性模型参数估计中白、 应用 中国农业科技 出版社 , , 一 章元明 动物生长摸型参数初值的探讨 , 中国农业科技出版社 , , 一 杨运清 , 刘 中源 家畜生态 , , 一 成 盆 赶由 刀、 峪 而 二 。。 下 汾 助 议 翻 , 气 ‘ 又 以 · 加 , , 、。 。 万卜 , 而 , · 灯 , , , 口