
第27卷第6期 作物学报 Vol.27.No.6 2001年11月 ACTA AGRONOMICA SINICA Nov.,200 回归分析中的模型偏差及其防止 莫惠栋 (扬州大学数量遗传研究室,江苏扬州225009》 提要研究了回归分析中的模型偏差(即分析模型和真实模型的差异)对估计数b和》的影响。结果 表明,偏差存在时b和》都成为有偏的估计数,也不能有效地测验回归均方的显著性。但是,如果在 试验的某些水平上适当地设置重复,而试验因子的水平数又多于要估计的回归参数数,就能够有效地 防止模型偏差。作为事例,评价了7个回归设计的优缺点。 关键词回归分析:模型偏差,偏差矩阵 Model Bias and Its Prevention in Regression Analysis MO Hui-Dong (Laboratory of Quantitatice Genetics.Yangshou University.Yangzhou 225009.China) Abstract The effect of model bias,i.e.,the difference between working model and true model in regression analysis,was investigated.The results indicated that the regression estimators,b and y,will become biased estimators and the significance of regression MS will not be tested validly when the model difference exists.However,this bias can be effectively prevented if the suitable replications on some experiment levels are set and the number of factor levels must as well be more than that of parameters estimated.As examples,the advantages and disadvantages of 7 regression designs were evaluated. Key words Regression analysis;Model bias;Bias matrix 1模型偏差的意义 在回归分析中,回归系数b=(6。,,b2,…,bw-1)是B=(3。,月,,,B-1)的无偏 估计数。因为当回归模型为: E(Y)=B。+月X1+,X:十…+P-X-1=1 (1) 时,B的最小平方估计数b为: b=(X'X)-X'Y. (2) (2)式中的X是不受期望影响的常量矩阵,而b和Y则是随机变数。因此可得: E(b)=(X'X)-X'E(Y)=(X'X)-X'XB=B. (3) (3)式中的(XX)-1X'X=1为p阶单位矩阵。 是日 39602-03-20 Received on:2001-02-09.Accepted on:2001-03-20
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 第 "#卷 第 $期 作 物 学 报 %&’("#)*&($ "++,年 ,,月 -./- -012*234.- 54*4.- *&6()"++, 回归分析中的模型偏差及其防止7 莫 惠 栋 8扬州大学数量遗传研究室)江苏扬州 ""9++:; 提 要 研究了回归分析中的模型偏差8即分析模型和真实模型的差异;对估计数 的影响?结果 表明)偏差存在时 都成为有偏的估计数)也不能有效地测验回归均方的显著性?但是)如果在 试验的某些水平上适当地设置重复)而试验因子的水平数又多于要估计的回归参数数)就能够有效地 防止模型偏差?作为事例)评价了 #个回归设计的优缺点? 关键词 回归分析@模型偏差@偏差矩阵 ABCDEFGHIHJCKLIMNDODJLGBJGJPDQNDIIGBJRJHESIGI 32TUVWX&YZ 8[\]^_\‘^_a^bcd\e‘f‘\‘fghiheh‘fjk)l\emno^dpefgh_kf‘a(l\emno^d""9++:)qofe\; RrILNHsL /tuuvvuwx&vy&zu’{V|})V(u()xtuzVvvu~uYwu{ux!uuY!&~"VYZy&zu’|Yzx~Uu y&zu’VY~uZ~u}}V&Y|Y|’#}V})!|}VY6u}xVZ|xuz(/tu~u}U’x}VYzVw|xuzxt|xxtu~uZ~u}}V&Y u}xVy|x&~}))!V’’{uw&yu{V|}uzu}xVy|x&~}|Yzxtu}VZYVvVw|Ywu&v~uZ~u}}V&Y$%!V’’ Y&x{uxu}xuz6|’Vz’#!tuYxtuy&zu’zVvvu~uYwuu&V}x}(T&!u6u~)xtV}{V|}w|Y{uuvvuwxV6u’# ’~u6uYxuzVvxtu}UVx|{’u~u’’Vw|xV&Y}&Y}&yuu&’u~VyuYx’u6u’}|~u}ux|YzxtuYUy{u~&v v|wx&~’u6u’}yU}x|}!u’’{uy&~uxt|Yxt|x&v’|~|yuxu~}u}xVy|xuz(-}u&|y’’u})xtu |z6|Yx|Zu}|YzzV}|z6|Yx|Zu}&v#~uZ~u}}V&Yzu}VZY}!u~uu6|’U|xuz( (DS)BNCI 1uZ~u}}V&Y|Y|’#}V}@3&zu’{V|}@*V|}y|x~V& + 模型偏差的意义 在回归分析中)回归系数 <,-8]+)],)]").)]/0,;是 1,-82+)2,)2").)2/0,;的无偏 估计数?因为当回归模型为3 48=;- 2+5 2,6,5 2"6"5 . 5 2/0,6/0,- 78e8/;18/8,; 8,; 时)1的最小平方估计数 <为3 <- 87,7;0, 7,=( 8"; 8";式中的 7是不受期望影响的常量矩阵)而 <和 =则是随机变数?因此可得3 48<;- 87,7;0, 7,48=;- 87,7;0, 7,71- 1( 89; 89;式中的87,7;0, 7,7-:为 /阶单位矩阵? 7 国家自然科学基金资助项目8*&(9:$#+9:,; 收稿日期3"++,W+"W+:)接受日期3"++,W+9W"+ 1uwuV6uz&Y3"++,W+"W+:)-wwu’xuz&Y3"++,W+9W"+ 万方数据

6期 莫惠栋:回归分析中的模型偏差及其防止 711 但是,如果Y依X的真实关系不是(1)式,而是 E(Y)=XxBxi)Xixo BiaxD (4) 这就意味着我们在分析模型式(1)中忽略了X'B项,含q个回归系数。它将会产生什么后果 呢可以导得: E(b)=(X'X)X'E(Y)=(X'X)X'(XB+X'B) =(X'X)-X'XB+(X'X)-X'XB.=B+AB.. ⊙ (5)式中的 A=(X'x)-X'X' (6) 称为混名矩阵或偏差矩阵(alias or bias matrix)们。 以上结果说明:只有在B”=0时(分析模型与真实模型相符),b才是B的无偏估计数: 如果B≠0(分析模型和真实模型不相符),b不再是B的无偏估计数。在后一种情况下,对 E(Y)的估计应是 =Xb+XAb, (7) 而不是 Y=Xb. (8) 这里的 (·-)=XAb (9) 就称为回归模型的偏差效应(bias effect)。 2模型偏差的估计 由于偏差效应XAb'是由B≠0产生的,所以一般化的方法是由(5)和(6)式估计模型偏 差。以下举两例说明。 2.1例1 设分析模型是E(Y)=月,十月X,(一元线性回归),而真实模型是E(Y)=B。十 3X1十B2X2(二元线性回归),并且X=(一1,0,1),X2=(0,1,0)。则应用分析模型会造成 怎样的偏差? 此例的情况是: 0 1 B X·B 由于 cx--- 故由(6)式得: 4-a- 再由(5)式得: 万方数据 -+a-+
但是!如果 "依 #的真实关系不是$%&式!而是 ’$(&) *$+,-&.$-,%&/ *0 $+,1&.0 $1,%&2 $3& 这就意味着我们在分析模型式$%&中忽略了 *0 .0项!含 1个回归系数4它将会产生什么后果 呢5可以导得6 ’$7&) $*8*&9% *8’$(&) $*8*&9% *8$*./ *0 .0 & ) $*8*&9% *8*./ $*8*&9% *8*0 .0 ) ./ :.0 2 $;& $;&式中的 :) $*8*&9% *8*0 $?=@ABC?=@D=EB?F&G%H 4 以上结果说明6只有在 .0 )I时$分析模型与真实模型相符&!7才是 .的无偏估计数J 如果 .0 KI$分析模型和真实模型不相符&!7不再是 .的无偏估计数4在后一种情况下!对 ’$(&的估计应是 ( L0 ) *7/ *:70 ! $M& 而不是 ( L) *72 $N& 这里的 $( L0 9 ( L&) *:70 $O& 就称为回归模型的偏差效应$C?=@PQQPRE&4 S 模型偏差的估计 由于偏差效应 *:70是由 .0 KI产生的!所以一般化的方法是由$;&和$<&式估计模型偏 差4以下举两例说明4 S2T 例 T 设分析模型是 ’$(&)UI/U%*%$一元线性回归&!而真实模型是 ’$(&)UI/ U%*%/UV*V$二元线性回归&!并且 *8 %)$9%!I!%&!*8 V)$I!%!I&4则应用分析模型会造成 怎样的偏差5 此例的情况是6 ’$(&) ’ "% "V " W X Y [Z ) % 9 % I % I % W X Y % % IZ UI U% U W X Y VZ ) % 9 % % I W X Y % %Z UI U W X Y %Z / W X Y Z I % I UV) *./ *0 .0 2 * . *0 .0 2 由于 $*8*&9%) [ I \I V] 9% ) %^[ I \I %^V]!*8*0 ) % % % \9 % I %] W X Y Z I % I ) \ ] % I 2 故由$<&式得6 :) %^[ I \I %^V]\ ] % I ) %^[ \I]2 再由$;&式得6 ’ _I _ W X Y %Z ) UI U W X Y %Z / %^[ \I ]UV) UI/ UV^[ U W X Y % Z J 即 <期 莫惠栋6回归分析中的模型偏差及其防止 M%% 万方数据

712 作 物 学 报 27卷 E(b)=B。+B2/3,E(b)=月1. 此例相当于数量遗传学中以加性模型分析具有加性一显性效应的试验结果,月,和B:分 别为加性和显性效应。以上结果说明,这时的b仍是3,的无偏估计:但b。(遗传背景效应) 却是B。的有偏估计,混杂有显性效应,其偏差为月/3。 2.2例2设分析模型是E(Y)=3。十3,X1,而真实模型是E(Y)=3。+3X,十B,X+3,X 且X1=(-3,-2,一1,0,1,2,3)。则应用分析模型会造成怎样的偏差? 「1-37 9 -27 -2 8 -1 -1 这里X= 1 0 、X=0 0 :并有 1 1 1 1 2 4 8 1 3J 9 27 -68 - 280 0196 故由(6)式可得: 4=xx-xx-g8-69 即有: E(b)=3。+4B2,E(b)=B1+7B3 所以。和b,都不是B。和B,的无偏估计数。 3 模型偏差的测验 回归分析中依变数Y的变异可能分解为三个部分,即:①纯误差均方MS:,它由X同 水平的重复间变异估计,具自由度dfg=三(m一I)(m,为X第i水平的重复次数,l为X的水 平数):②模型偏差均方MS,它因分析模型缺失X'B项引起,又称失拟(lack of fit)均方, 具自由度df=(1一p)(p为分析模型的参数数目):③回归均方MSR,它因X的水平不同引 起,具dfe=(p一1)。可以导出以上各个均方的期望均方(EMS)为四: EMSE= EMS=+(B)'(X*-XA)'(X'-XA)B/(-B)] (10) EMSR=2+{(XB+XB)'[X(X'X)-1X'-11/m](XB+XB)/(p-1) (10)式表明: (1)由 F=MSB/MS (11) 可测验H。·B=0,即测验分析模型是否存在偏差?如果接受B°=0,表明不存在偏差,且 MS和MSg同义,都是估计a2;如果否定B=0,表明分析模型需要增添X·B项后再分析。 (2)当接受H。:B=0时,(10)式的EMSR=G2+{BX[X(X'X)-1X'-1/m]XB/(p 1)》,故由万方数据 F MSk/MSE F MSk/(MSE+MS 1:) (12)
!"#$%& ’$( ’)*+,!"#-%& ’-. 此例相当于数量遗传学中以加性模型分析具有加性/显性效应的试验结果,’-和 ’)分 别为加性和显性效应0)1 2以上结果说明,这时的 #-仍是 ’-的无偏估计3但 #$"遗传背景效应% 却是 ’$的有偏估计,混杂有显性效应,其偏差为 ’)*+2 4.4 例 4 设分析模型是 !"5%&’$(’-6-,而真实模型是 !"5%&’$(’-6-(’)6) -(’+6+ -, 且 67 -&"8+,8),8-,$,-,),+%2则应用分析模型会造成怎样的偏差9 这里 6& - 8 + - 8 ) - 8 - - $ - - - ) : ; & ? 8 )@ A 8 B - 8 - $ $ - - A B : ; & )B $ C$ -?ED. 故由"E%式可得F G& "676%8- 676> & -*@ $ C$ -*)BD )B $ C$ -?ED& A $ C$ @D, 即有F !"#$%& ’$( A’),!"#-%& ’-( @’+. 所以 #$和 #-都不是 ’$和 ’-的无偏估计数2 H 模型偏差的测验 回归分析中依变数 I的变异可能分解为三个部分,即FJ 纯误差均方 KLM,它由 N 同 水平的重复间变异估计,具自由度 OPM& Q R S&- "TS8-%"TS为 N第 S水平的重复次数,R为 N的水 平数%3U 模型偏差均方 KLV,它因分析模型缺失 6> W >项引起,又称失拟"XYZ[\]]^_%均方, 具自由度 OPV&"R8‘%"‘为分析模型的参数数目%3a 回归均方 KLb,它因 N的水平不同引 起,具 OPb&"‘8-%2可以导出以上各个均方的期望均方"MKL%为0-1 F MKLM & c) MKLV & c)( 0"W> %7"6> 8 6G%7"6> 8 6G%W> *"R8 ‘%1 MKLb & c)( d"6W( 6> W> %706"676%8- 678 ee7*f1"6W( 6> W> g h %*"‘8 -%ji "-$% "-$%式表明F "-%由 k&KLV*KLM "--% 可测验 l$mW> &$,即测验分析模型是否存在偏差9如果接受 W > &$,表明不存在偏差,且 KLV 和 KLM 同义,都是估计 c ) 3如果否定 W > &$,表明分析模型需要增添 6> W >项后再分析2 ")%当接受 l$mW > &$时,"-$%式的 MKLb&c ) (dW76706"676%8- 678ee7*f16W*"‘8 -%j,故由 k& KLb*KLM 或 k& KLb*"KLM ( KLV% "-)% @-) 作 物 学 报 )@卷 万方数据

6期 莫惠栋:回归分析中的模型偏差及其防止 713 可测验H。:B=0。 (3)当否定H。B°=0时,F=MSR/MSE或F=MSk/MSB对于测验H。:B=0均属无 效。 4通过试验设计防止模型偏差 上述理论结果表明,回归模型偏差对试验结果的正确分析会有严重干扰。为避免模型偏 差,在回归设计上应当要求:①必须在X的各个水平或某些水平上设置重复以估计MS:② 必须使(试验水平数)>p(分析模型的参数数)以估计和测验MS,即测验是否存在模型偏 差(失拟)以及在必要时可扩展分析模型、消除偏差。下面列举7种设计作具体评价。为了 般化,我们用X=(1,一1,0)依次表示试验因子X的高水平、低水平和中点值:并假设分析 模型是E(Y)=3。十月,X,用回归系数b,的标准误相当于σ的倍数,即 5%,/a=1/x (13) 表示设计精度(s%/σ愈小,设计精度愈高)。 设计1:以d=2/(1-1)=2/(10-1)=0.22为间距,在X=(±0.11,±0.33,±0.55. 士0.77,士1.00)上各设置1水平,共10个水平:1次重复。 设计1:以d=2/(5-1)=0.5为间距,在X=(0,士0.5,士1.0)上各设置1个水平,共 5个水平:2次重复。 设计■:以d=2/(4-1)=0.66为间距,在X=(士0.33,士1.00)上各设置1水平,共4 个水平,其中X=(士0.33)上各重复4次,X=(士1.00)上各重复1次。 设计N:间距和水平同设计Ⅱ但在X=(土0.33)上各重复1次,在X=(土1.00)上各 重复4次。 设计V:以d=2/(3-1)=1.00为间距,在X=(0,士1.0)上各设置1水平,共3个水 平;其中X=0上重复6次,X=(士1.0)上各重复2次。 设计M:间距和水平同设计V;但在X=0上重复2次,在X=(士1.0)上各重复4次。 设计M:以d=2/(2-1)=2为间距,在X=(士1.0)上各设置1水平,共2个水平;重 复5次。 上述设计的几何解释示于图1,其设计参数则列于表1。表1说明: (1)设计1是不可取的,它虽有10个试验水平,却不能估计MS:。试验1也是不可取 的,它虽然精度最高(对于分析模型),但不能估计MS,不能发现可能存在的模型偏差。 (2)设计I~I都能够估计MSE和MS。如果存在MS:,它们都可能扩展分析模型,其 中设计1可扩展3项,设计I和W为2项,设计V和M为1项。但设计W的精度最高,又有稳 键的扩展空间,故为此处7种设计中的最佳设计:其次为设计M。 (3)设计1和N的试验水平和重复次数完全相同,但N的设计精度远高于Ⅱ:同理,设 计V和M的试验水平也完全相同,但M的设计精度远高于V。造成此种差异的原因是N和M 在端点水平上有较多次重复,而Ⅱ和V则在中心点或近中心点上有较多次重复。设置在端点 水平上的重复增大了(13)式中的x2值,故能够最大程度地提高设计精度。以往反应面方法 中的各种回归设计,几乎都是将重复设置在中心点上[3~]。这对估计MSg当然并无问题,但 非常不利韦捷离接计精度,是亟待改进的
可测验 !"#$%"& ’()当否定 !"#$* %"时+,%-./0-.1 或 ,%-./0-.2 对于测验 !"#$%"均属无 效& 3 通过试验设计防止模型偏差 上述理论结果表明+回归模型偏差对试验结果的正确分析会有严重干扰&为避免模型偏 差+在回归设计上应当要求45 必须在 6的各个水平或某些水平上设置重复以估计 -.178 必须使 9’试验水平数):;’分析模型的参数数)以估计和测验 -.2+即测验是否存在模型偏 差’失拟)以及在必要时可扩展分析模型+?>+")依次表示试验因子 6的高水平D+用回归系数 E>的标准误相当于 F的倍数+即 GE>0F% >0JHIK ’>() 表示设计精度’GE>0F愈小+设计精度愈高)& 设计L4以 M%K0’9?>)%K0’>"?>)%"NKK为间距+在 6%’O"N>>+O"N((+O"NPP+ O"N==+O>N"")上各设置 >水平+共 >"个水平7>次重复& 设计Q4以 M%K0’P?>)%"NP为间距+在 6%’"+O"NP+O>N")上各设置 >个水平+共 P个水平7K次重复& 设计R4以 M%K0’S?>)%"NTT为间距+在 6%’O"N((+O>N"")上各设置 >水平+共 S 个水平7其中 6%’O"N(()上各重复 S次+6%’O>N"")上各重复 >次& 设计U4间距和水平同设计R7但在 6%’O"N(()上各重复 >次+在 6%’O>N"")上各 重复 S次& 设计V4以 M%K0’(?>)%>N""为间距+在 6%’"+O>N")上各设置 >水平+共 (个水 平7其中 6%"上重复 T次+6%’O>N")上各重复 K次& 设计W4间距和水平同设计V7但在 6%"上重复 K次+在 6%’O>N")上各重复 S次& 设计X4以 M%K0’K?>)%K为间距+在 6%’O>N")上各设置 >水平+共 K个水平7重 复 P次& 上述设计的几何解释示于图 >+其设计参数则列于表 >&表 >说明4 ’>)设计L是不可取的+它虽有 >"个试验水平+却不能估计 -.1&试验X也是不可取 的+它虽然精度最高’对于分析模型)+但不能估计 -.2+不能发现可能存在的模型偏差& ’K)设计QYW都能够估计 -.1 和 -.2&如果存在 -.2+它们都可能扩展分析模型+其 中设计Q可扩展 (项+设计R和U为 K项+设计V和W为 >项&但设计U的精度最高+又有稳 健的扩展空间+故为此处 =种设计中的最佳设计7其次为设计W& ’()设计R和U的试验水平和重复次数完全相同+但U的设计精度远高于R7同理+设 计V和W的试验水平也完全相同+但W的设计精度远高于V&造成此种差异的原因是U和W 在端点水平上有较多次重复+而R和V则在中心点或近中心点上有较多次重复&设置在端点 水平上的重复增大了’>()式中的 ZIK值+故能够最大程度地提高设计精度&以往反应面方法 中的各种回归设计+几乎都是将重复设置在中心点上[(YT\ &这对估计 -.1 当然并无问题+但 非常不利于提高设计精度+是亟待改进的& T期 莫惠栋4回归分析中的模型偏差及其防止 =>( 万方数据
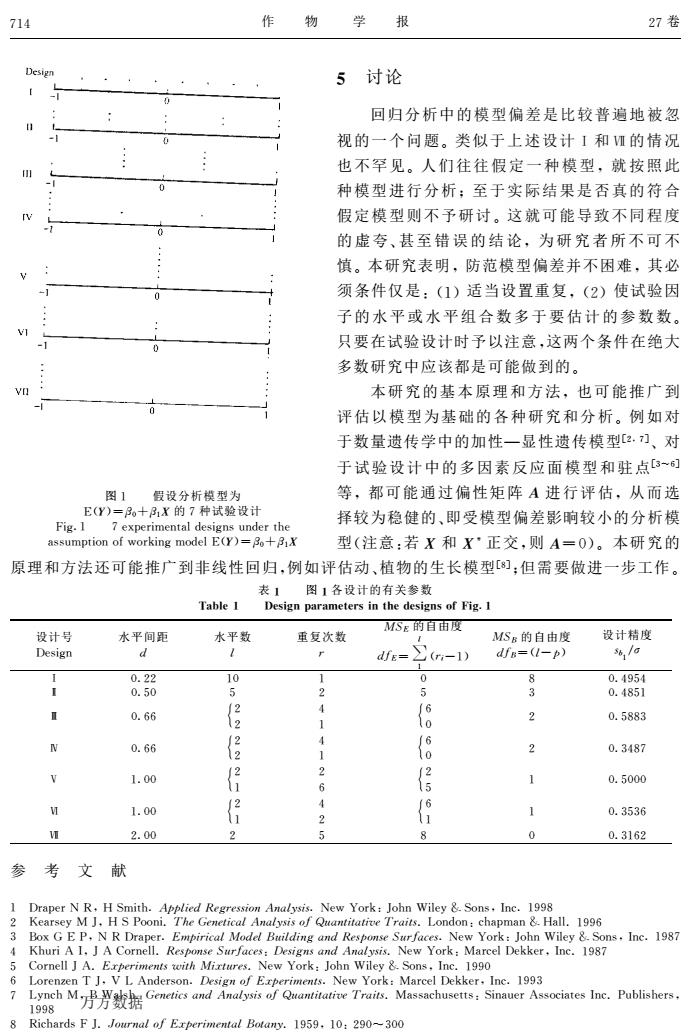
714 学 报 27卷 5讨论 回归分析中的模型偏差是比较普遍地被忽 视的一个问题。类似于上述设计1和Ⅶ的情况 也不罕见。人们往往假定一种模型,就按照此 种模型进行分析;至于实际结果是否真的符合 假定模型则不予研讨。这就可能导致不同程度 的虚夸、甚至错误的结论,为研究者所不可不 慎。本研究表明,防范模型偏差并不困难,其必 须条件仅是:1)适当设置重复,(2)使试验因 子的水平或水平组合数多于要估计的参数数。 只要在试验设计时予以注意,这两个条件在绝大 多数研究中应该都是可能做到的。 本研究的基本原理和方法,也可能推广到 评估以模型为基础的各种研究和分析。例如对 于数量遗传学中的加性一显性遗传模型2.门、对 于试验设计中的多因素反应面模型和驻点~司 图1假设分析模型为 等,都可能通过偏性矩阵A进行评估,从而选 E(Y)+AX的7种试验设计 择较为稳健的、即受模型偏差影响较小的分析模 Fig.I 型(注意:若X和X·正交,则A=0)。本研究的 原理和方法还可能推广到非线性回归,例如评估动、植物的生长模型[®;但需要做进一步工作。 表1图1各设计的有关参数 Table 1 Design parameters in the designs of Fig.1 设计号 水平间距 水平数 重复次数 MSE的自由度 MS的自由度 设计精度 Design d dfe->(n-D) dfs=(1-p) 6,/a 分 83 & 0.66 (8 0.5883 0.66 2 0.3487 1.00 后 0.5000 1.00 0.3536 2.00 2 0.3162 参考文献 Draper NR.HSmith.Applied Regrei Analysis.New York:John Wiley &.Sons.Ine.1998 Empirical Mod .1096 ,lnc.1987 Khuri A 1.JA Cornell.R e Surfaces:Desig New York:Ma rcel Dekker.Inc.1987 w York: ne.1993 Richards FJ.Journal of Erperimental Botany.1959.10:290-300
图 ! 假设分析模型为 "#$%&’()’!*的 +种试验设计 ,-./! +01203-40567890:-.5:;59036?=3@-5.4=908"#$%&’()’!* A 讨论 回归分析中的模型偏差是比较普遍地被忽 视的一个问题B类似于上述设计C和D的情况 也不罕见B人们往往假定一种模型E就按照此 种模型进行分析F至于实际结果是否真的符合 假定模型则不予研讨B这就可能导致不同程度 的虚夸G甚至错误的结论E为研究者所不可不 慎B本研究表明E防范模型偏差并不困难E其必 须条件仅是H#!%适当设置重复E#I%使试验因 子的水平或水平组合数多于要估计的参数数B 只要在试验设计时予以注意E这两个条件在绝大 多数研究中应该都是可能做到的B 本研究的基本原理和方法E也可能推广到 评估以模型为基础的各种研究和分析B例如对 于数量遗传学中的加性J显性遗传模型KIE+L G对 于试验设计中的多因素反应面模型和驻点KMNOL 等E都可能通过偏性矩阵 P进行评估E从而选 择较为稳健的G即受模型偏差影晌较小的分析模 型#注意H若 *和 *Q正交E则 P&(%B本研究的 原理和方法还可能推广到非线性回归E例如评估动G植物的生长模型KRL F但需要做进一步工作B 表 S 图 S各设计的有关参数 TUVWXS YXZ[\]^U_U‘XaX_Z[]abXcXZ[\]Zdef[\/S 设计号 g0:-.5 水平间距 h 水平数 i 重复次数 j klm的自由度 hnm&o i ! #jpq!% klr的自由度 hnr&#iqs% 设计精度 tu! vw C (/II !( ! ( R (/xyzx { (/z( z I z M (/xRz! | (/OO } I I x ! } O ( I (/zRRM ~ (/OO } I I x ! } O ( I (/MxR+ ! !/(( } I ! I O } I z ! (/z((( " !/(( } I ! x I } O ! ! (/MzMO D I/(( I z R ( (/M!OI 参 考 文 献 ! g37203# $E% &4-6?-,?-,<p<-<p@(9j-p<t/77::75<;:066:H&-57;03E::=5-760:455/8;M8-:<03:E !yyR R $-5<739:,0/N+?j,-i+nmHs(jpD(,<-ir+<-,./!yzyE!(HIy(NM(( +!x 作 物 学 报 I+卷 万方数据

回归分析中的模型偏差及其防止 日万方数据文成线桃 作者: 莫惠栋 作者单位: 扬州大学数量遗传研究室。 刊名: 作物学报STI©PK) 英文刊名: ACTA AGRONOMICA SINICA 年,卷(明) 2001,27(6) 引用次数: 2次 考文献(8条) 1.Draper N RH Smith Applied Regression Analysis 1998 2.Kearsey M J.H S Pooni The Genetical Analysis of Quantitative Traits 1996 3.BOX G E P.N R Draper Empirical Model Building and Response Surfaces 1987 4.Khuri A I.J A Cornell Response Surfaces:Designs and Analysis 1987 5.Cornell J A Experiments with Mixtures 1990 6.Lorenzen T J.V L Anderson Design of Experiments 1993 7.Lynch MB Walsh Genetics and Analysis of Quantitative Traits1998 &.Richards F」查看详情1959 相似文献(0条) 引证文献(2条) 1.刘华卷烟材料与焦油量关系的回归设计与分析[期刊论文]-烟草科技2008(05) 2.莫惠栋配料混合试验的设计和分析(续)[期刊论文]-扬州大学学报(农业与生命科学版 2004(02) 本文链接:http:/,wanfangdata.com.cn/Periodical_zuowxb200106005.aspx 下载时间:2010年3月5日
回归分析中的模型偏差及其防止 作者: 莫惠栋 作者单位: 扬州大学数量遗传研究室, 刊名: 作物学报 英文刊名: ACTA AGRONOMICA SINICA 年,卷(期): 2001,27(6) 引用次数: 2次 参考文献(8条) 1.Draper N R.H Smith Applied Regression Analysis 1998 2.Kearsey M J.H S Pooni The Genetical Analysis of Quantitative Traits 1996 3.BOX G E P.N R Draper Empirical Model Building and Response Surfaces 1987 4.Khuri A I.J A Cornell Response Surfaces: Designs and Analysis 1987 5.Cornell J A Experiments with Mixtures 1990 6.Lorenzen T J.V L Anderson Design of Experiments 1993 7.Lynch M.B Walsh Genetics and Analysis of Quantitative Traits 1998 8.Richards F J 查看详情 1959 相似文献(0条) 引证文献(2条) 1.刘华 卷烟材料与焦油量关系的回归设计与分析[期刊论文]-烟草科技 2008(05) 2.莫惠栋 配料混合试验的设计和分析(续)[期刊论文]-扬州大学学报(农业与生命科学版) 2004(02) 本文链接:http://d.g.wanfangdata.com.cn/Periodical_zuowxb200106005.aspx 下载时间:2010年3月5日