
第九章 检测理论 实际中经常需要根据观测波形对几种可能的情况进行 判决,如在雷达信号检测中,根据雷达接收机输出的波形作 出目标存在与否的判断。由于存在一定的环境杂波干扰以及 雷达接收机内部的噪声,微弱的雷达回波信号总是淹没在杂 波和噪声中(通常把杂波和噪声统称为噪声),因此,雷达 信号的检测就是从含有噪声的数据(观测)中判断是否有目 标回波信号存在。在数字通信系统中,数字0和数字1是用 两个不同信号来表示的,信号在信道中传输会叠加上信道噪 声,通信信号的检测就是从含有噪声的数据(观测)中区分 两种不同的信号。噪声中信号检测的理论基础是假设检验理 论,因此,本章首先介绍假设检验的基本概念和基本判决准 则,再将假设检验理论应用于噪声中信号的检测
第九章 检测理论 实际中经常需要根据观测波形对几种可能的情况进行 判决,如在雷达信号检测中,根据雷达接收机输出的波形作 出目标存在与否的判断。由于存在一定的环境杂波干扰以及 雷达接收机内部的噪声,微弱的雷达回波信号总是淹没在杂 波和噪声中(通常把杂波和噪声统称为噪声),因此,雷达 信号的检测就是从含有噪声的数据(观测)中判断是否有目 标回波信号存在。在数字通信系统中,数字0和数字1是用 两个不同信号来表示的,信号在信道中传输会叠加上信道噪 声,通信信号的检测就是从含有噪声的数据(观测)中区分 两种不同的信号。噪声中信号检测的理论基础是假设检验理 论,因此,本章首先介绍假设检验的基本概念和基本判决准 则,再将假设检验理论应用于噪声中信号的检测

9.1假设检验的基本概念 信号检测理论是在假设检验的基础上发展起来的,所谓假设是可能判决结果的陈述, 根据观测对几种假设作出判决称为假设检验。如雷达信号的检测问题,“目标存在”、“目 标不存在”是雷达信号检测的两种可能结果,用H。表示“目标不存在”,用H1表示“目标 存在”,H。和H1是雷达信号检测提出的两种假设,通常称H。为原假设(或零假设), H1为备选假设。对应于每一种假设,都有一个观测,观测是随机变量。如雷达信号检测, 在H。假设下没有目标,雷达接收机的输出只有噪声,在H1假设下,接收机输出为信号 加噪声。因此观测接收机的输出波形,得到观测为 Ho:Z=v H1:z= 其中v代表噪声,s代表信号,由于噪声v是随机变量,所以观察z也是随机变量。观 测可能是单次观测,也可能是多次观测,对于多次观测,可以用观测矢量表示,即
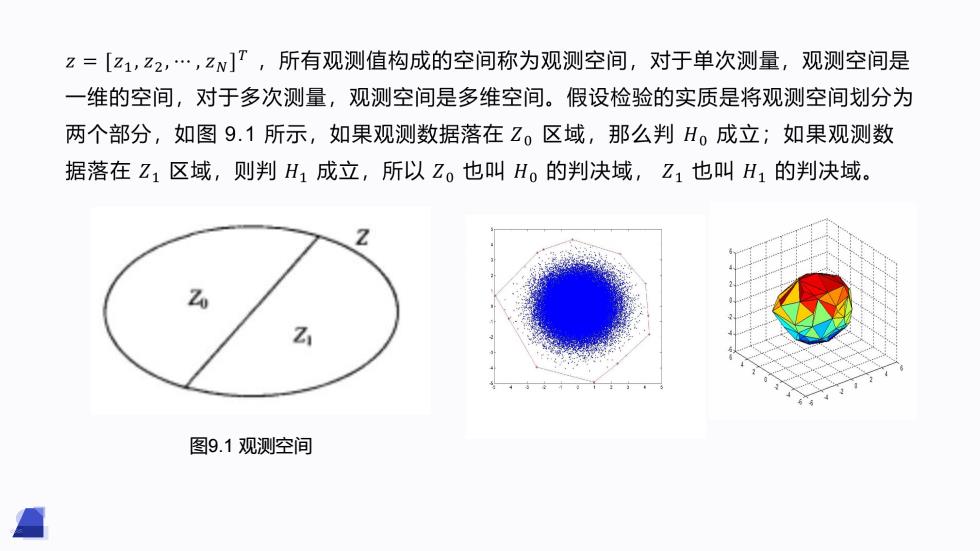
z=[z1,z2,…,zw]T,所有观测值构成的空间称为观测空间,对于单次测量,观测空间是 一维的空间,对于多次测量,观测空间是多维空间。假设检验的实质是将观测空间划分为 两个部分,如图9.1所示,如果观测数据落在Z。区域,那么判H。成立;如果观测数 据落在Z1区域,则判H1成立,所以Z。也叫H。的判决域,Z1也叫H1的判决域。 Z 图9.1观测空间
图9.1 观测空间

为了获得好的判决性能,不能随意划分观测空间,必须按照一定的准则来进行划分。 比如,可以按照后验概率的大小来进行划分。在得到观测z的情况下,可以计算两种假 设的后验概率P(H1lz)、P(Hoz)比较两个后验概率的大小,判后验概率大所对应的那 个假设成立,称为最大后验概率准则。即 P(H1IZ) Hi 1 P(Holz)Ho (9.1.1) 由贝叶斯公式得 P(Hilz)= P(zHDP(Hi) (i=0,1) (9.1.2) f(z) 代人(9.1.1)式,可得 f(zIH) Hi f(z|Ho) P(Ho) P(H1) (9.1.3) Ho 式中P(zlH)称为似然函数,△(a)=称为似然比,o=P(H)/P(H1)称为判决门 P(zHo) 限,由(9.1.3)式可以看出,判决表达式是似然比检验的形式,即似然比与门限进行比 较

H A(z)≥n0 (9.1.4) Ho 对于二元假设检验问题,在进行判决时可能发生下列四种情况: (1)H。为真,判Ho成立; Ho H (2)H1为真,判H1成立; Ho 正确 虚警概率 H 漏检概率 检测概率 (3)H。为真,判H1成立 (4)H1为真,判H。成立。 第(1)、(2)种判决属于正确判决,第(3)种判决是一种错误判决,称为第一 类错误,按雷达的术语称为虚警,虚警概率为 Pr P(DiIHo)=ff(zIHo)dz (9.1.5) 第(4)种判决也是一种错误判决,称为第二类错误,按雷达的术语称为漏警,漏警概率为
H0 H1 H0 正确 虚警概率 H1 漏检概率 检测概率

PM P(DoH1)=Jf(ZIH1)dz (9.1.5) 在(9.1.5)式和(9.1.6)式中,D1和Do分别表示判H1成立和判H。成立。总的错误 概率为 Pe P(D1,Ho)+P(Do,H1)=PFP(Ho)+PMP(H1) (9.1.7) 第(2)种判决按雷达的术语称为检测,检测概率为 PD P(D1H)=f(zH1)dz (9.1.8) 检测概率与漏警概率之间存在如下关系 PD PM=1 (9.1.9)

例9.1 设有两种假设 K(2H) Ho:Z=v H1:z=1+v 其中v~N(0,1),假定P(Ho)=P(H1),求最大后验概率准则的判决表达式,并确定判 决性能 解 最大后验概率准则的判决表达式是似然比检验的形式,因此首先计算似然比 (如图9.2所示),即 feH=a(2”) )-PM m惯=epa-2

所以判决表达式为 1 H1 exp (z- ≥1 Ho 对上式两边取对数并经整理后可得判决表达式为 H z2 1 Ho 在本例中,观测空间Z=(-∞,+o),H。的判决域为Z0=(-∞,1/2),H1的判决域为 Z0=(1/2,+∞),判决的虚警概率为 Pr P(D.U)a I t)ds =怎n()虹=0吃

其中 Q()=exp(-u2/2)du (9.1.10) 为正态概率右尾函数。漏警概率为 Pw-P(D )dz -良.高m-e-t网-0网 检测概率为 PD=P(D1lH1)=1-PM=1-Q(1/2)

(9.1.4)式是根据单次测量得出的,对于多次测量,只需把测量z改写成矢量形式z就可 以了,这时的概率密度是多维概率密度,即判决表达式为 Hi A(z)10 (9.1.11) Ho 其中 A)=品=治 P(z1,z2,…,zNHo) (9.1.12) 虚警概率为 Pr=∫2,f(z|Ho)dz=J2,f(z1,z2,…,zNHo)dz1,z2,…,zN (9.1.13) 漏警概率为 PM=J2。f(z|H1)dz=∫2nf(z1,z2,…,zNlH1)dz1,z2,…,zN (9.1.14)