
第三章 离散趋势的统计描述 第一节 变异程度(离散程度)的指标 第二节 正态分布及应用 第三节 医学参考值范围

极差和四分位数间距 极差 (全距) R二最大值-最小值 R大说明变异程度大,反之说明变异程度小 四分位数间距 Q=P5-P25 Q大说明数据的变异越大,反之说明数据的 变异程度小
◼ 极差(全距) ◼ R = 最大值 – 最小值 ◼ R大说明变异程度大,反之说明变异程度小 ◼ 四分位数间距 ◼ Q = P75 – P25 ◼ Q大说明数据的变异越大,反之说明数据的 变异程度小。 一、极差和四分位数间距

二、离均差平方和、方差、 标准差和变异系数 (一)平均偏差 (二)离均差平方和 (三)方差 (四)标准差 (五)变异系数
二、离均差平方和、方差、 标准差和变异系数 (一)平均偏差 (二)离均差平方和 (三)方差 (四)标准差 (五)变异系数

平均偏差= ∑x- n 离均差平方和-∑(-寸=公② 方差2=∑(x- 记住! 自由度V=-1随机变量能自由取值的个数 MS也可以表示为方差。S大数据的变异越大
n x − x 平均偏差= ( ) ( ) n x x x x 2 2 2 离均差平方和= − = − ( ) 1 2 2 − − = n x x 方差s 自由度 ν= n-1 随机变量能自由取值的个数 MS 也可以表示为方差。S大数据的变异越大 记住!
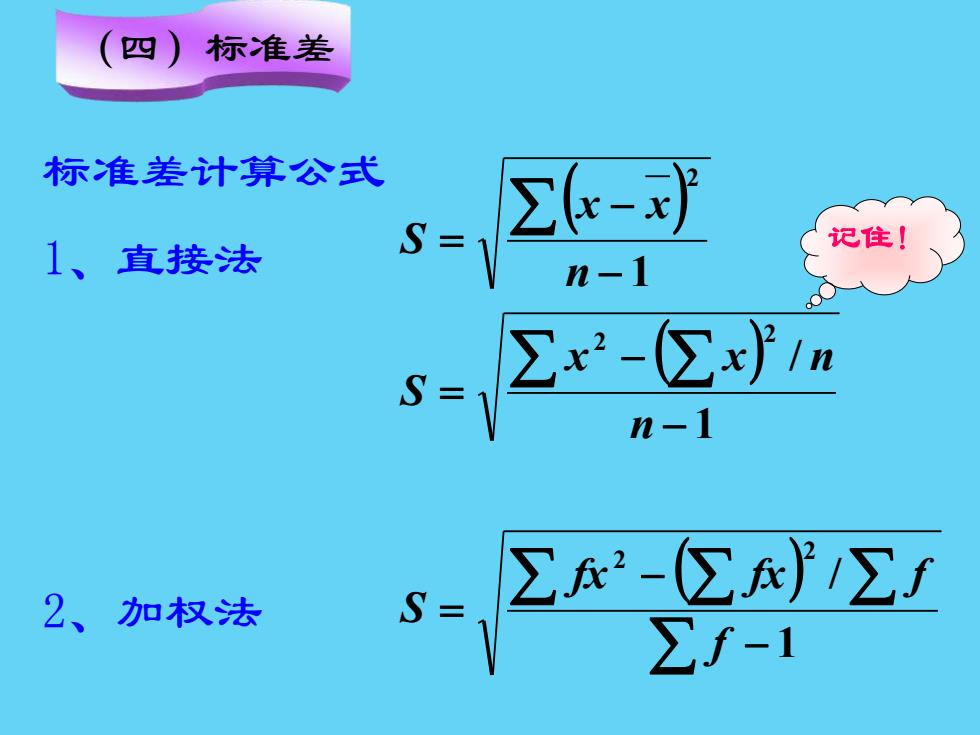
(四) 标准差 标准差计算公式 ∑c-可 1、直接法 S=n-1 记住! S-1 2-②m n-1 s ∑x2-(∑}∑f 2、加权法 ∑f-1
标准差计算公式 1、直接法 2、加权法 ( ) ( ) ( ) − − = − − = − − = 1 / 1 / 1 2 2 2 2 2 f fx fx f S n x x n S n x x S 记住! (四)标准差

■ 例题1、对甲乙两名高血压患者连续观察5 天,测得的收缩压分别为 甲患者(mmHg)162145 178142186 乙患者(mmHg)164160163159166 计算标准差? x甲=162.6 x乙=162.4
◼ 例题1、对甲乙两名高血压患者连续观察5 天,测得的收缩压分别为 甲患者 (mmHg) 162 145 178 142 186 乙患者 (mmHg) 164 160 163 159 166 计算标准差? 162.4 162.6 = = 乙 甲 x x

甲患者∑x=162+145+178+142+186=813 ∑x2=1622+1452+1782+1422+1862=133713 133713-8132/5 S= =19.49 5-1 乙患者:∑x=164+160+163+159+166=812 ∑x2=1642+1602+1632+1592+1662=131902 S 131902-8122/5 =2.88 5-1
2.88 5 1 131902 812 / 5 164 160 163 159 166 131902 164 160 163 159 166 812 19.49 5 1 133713 813 / 5 162 145 178 142 186 133713 162 145 178 142 186 813 2 2 2 2 2 2 2 2 2 2 2 2 2 2 = − − = = + + + + = = + + + + = = − − = = + + + + = = + + + + = S x : x S x : x 乙患者 甲患者
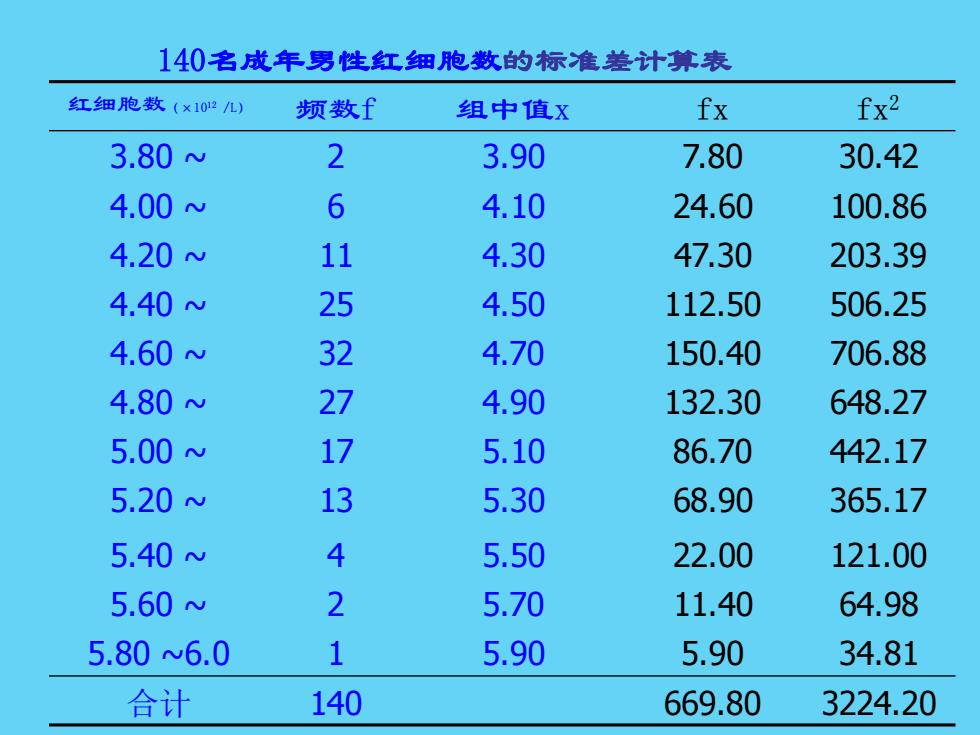
140名成年男性红细胞数的标准差汁算表 红细胞数(x102L) 频数f 组中值X fx fx2 3.80 2 3.90 7.80 30.42 4.00 6 4.10 24.60 100.86 4.20 11 4.30 47.30 203.39 4.40 25 4.50 112.50 506.25 4.60 32 4.70 150.40 706.88 4.80 27 4.90 132.30 648.27 5.00w 17 5.10 86.70 442.17 5.20N 13 5.30 68.90 365.17 5.40N 4 5.50 22.00 121.00 5.60N 2 5.70 11.40 64.98 5.806.0 1 5.90 5.90 34.81 合计 140 669.80 3224.20
140名成年男性红细胞数的标准差计算表 红细胞数(×1012 /L) 频数f 组中值x fx fx2 3.80 ~ 2 3.90 7.80 30.42 4.00 ~ 6 4.10 24.60 100.86 4.20 ~ 11 4.30 47.30 203.39 4.40 ~ 25 4.50 112.50 506.25 4.60 ~ 32 4.70 150.40 706.88 4.80 ~ 27 4.90 132.30 648.27 5.00 ~ 17 5.10 86.70 442.17 5.20 ~ 13 5.30 68.90 365.17 5.40 ~ 4 5.50 22.00 121.00 5.60 ~ 2 5.70 11.40 64.98 5.80 ~6.0 1 5.90 5.90 34.81 合计 140 669.80 3224.20
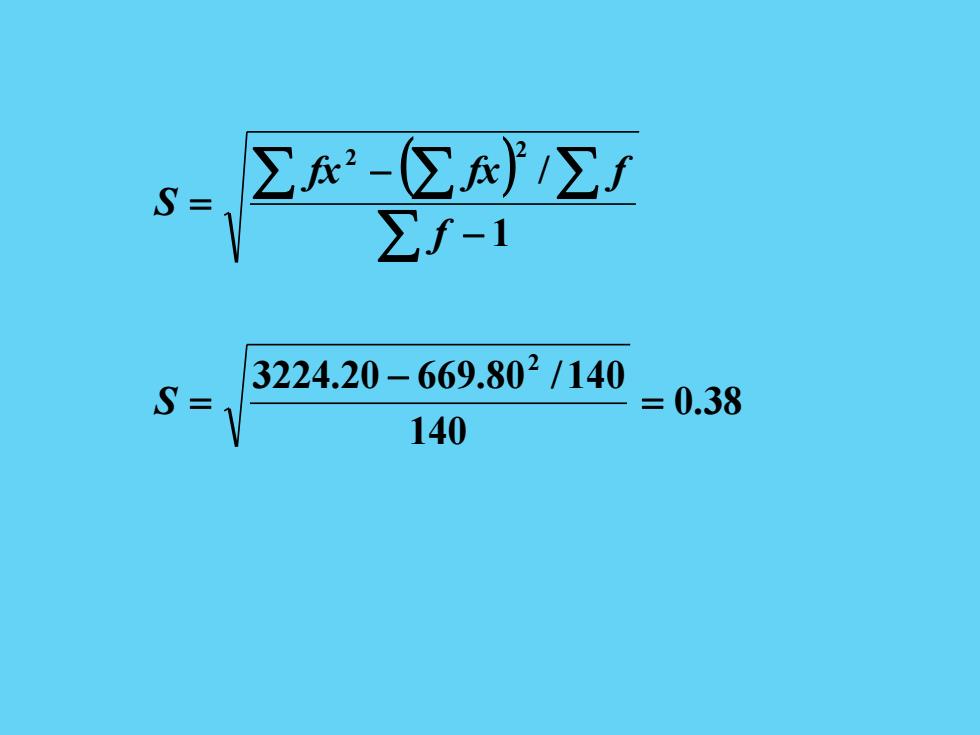
∑R2-∑R∑f Σf-1 3224.20-669.802/140 =0.38 140
( ) 0.38 140 3224.20 669.80 /140 1 / 2 2 2 = − = − − = S f fx fx f S
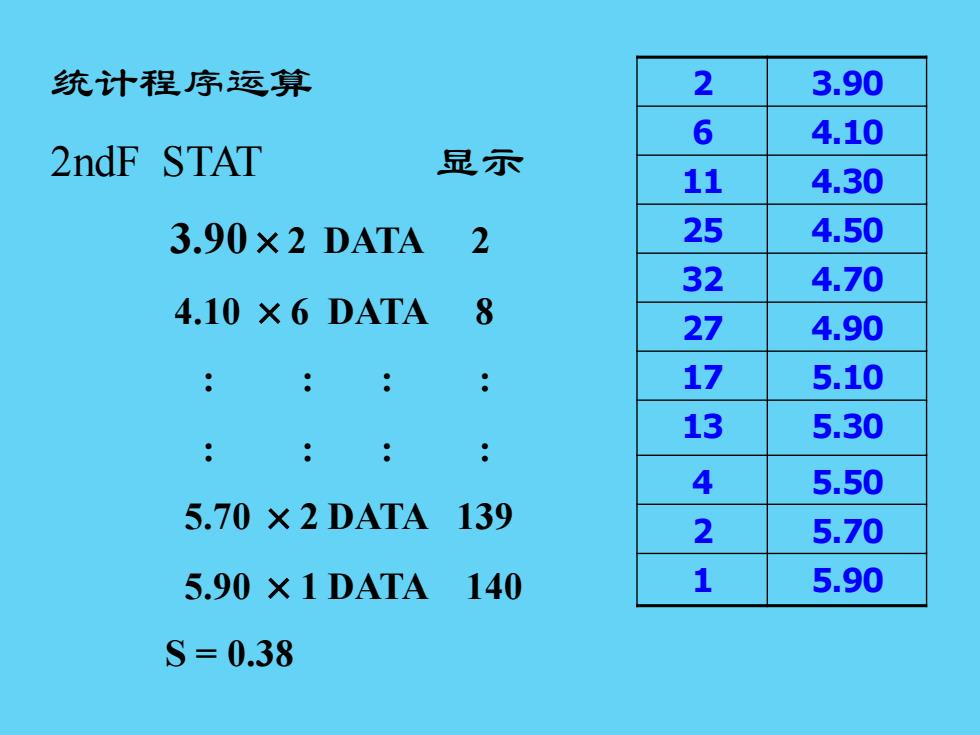
统计程序运算 2 3.90 6 4.10 2ndF STAT 显示 11 4.30 3.90×2DATA 2 25 4.50 32 4.70 4.10×6DATA 8 27 4.90 17 5.10 13 5.30 4 5.50 5.70×2DATA139 2 5.70 5.90×1DATA140 1 5.90 S=0.38
统计程序运算 2ndF STAT 显示 3.90×2 DATA 2 4.10 ×6 DATA 8 : : : : : : : : 5.70 ×2 DATA 139 5.90 ×1 DATA 140 S = 0.38 2 3.90 6 4.10 11 4.30 25 4.50 32 4.70 27 4.90 17 5.10 13 5.30 4 5.50 2 5.70 1 5.90