
离散随机变量及分布律 定义 若随机变量X的可能取值是有限 个或可列个,则称X为离散型随机变量 描述X的概率特性常用概率分布或分布律 即 P(X=xx)=Pk,k=1,2,… 或 X x2…Xk P1p2·P%
定义 若随机变量 X 的可能取值是有限 个或可列个, 则称 X 为离散型随机变量 描述X 的概率特性常用概率分布或分布律 P(X = xk ) = pk , k =1,2, X x1 x2 xk P p1 p2 pk 或 离散随机变量及分布律 即

或 分布律的性质 P%≥0,k=1,2,… 非负性 归一性
分布律的性质 ❑ pk 0, k =1,2, 非负性 ❑ 1 1 = k= k p 归一性 或 X ~ x1 x2 xk p1 p2 pk

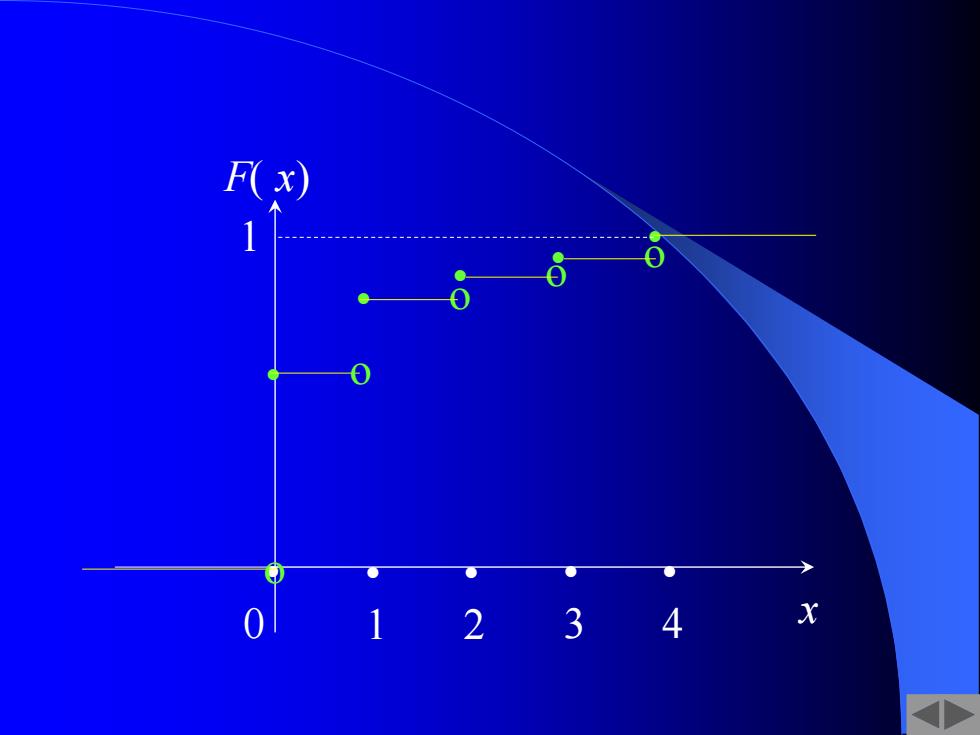
离散随机变量及分布函数 F(x)=P(X≤x)=P(X=x) Xk≤X ∑P(X=x)=∑P X≤X Xk≤X Pk=PX=x)=(x)-F(x-) 其中X-1<Xk F(x)是分段阶梯函数,在X的可能取 值x处发生间断,间断点为第一类跳趺间 断点,在间断点处有跃度Pk:
F( x) 是分段阶梯函数, 在 X 的可能取 值 xk 处发生间断, 间断点为第一类跳跃间 断点,在间断点处有跃度 pk . 离散随机变量及分布函数 ( ) ( ) ( ) k = = k = k − k−1 p P X x F x F x ( ) ( ) (( )) x x k k F x P X x P X x = = = = = = x x k x x k k k P(X x ) p 其中 . k k x x −1
4
• 0 •1 •2 •3 •4 x F( x ) o• o 1 • • o• o• o

常见离散r.v.的分布 (1)0-1分布 X=Xk 0<p<1 P 1-P 或P(X=k)=p1-p),k=0,1 应用 凡试验只有两个结果,常用0-1 场合 分布描述,如产品是否合格、人 口性别统计、系统是否正常、电力消耗 是否超标等等
(1) 0 – 1 分布 ( ) (1 ) , 0,1 1 = = − = − P X k p p k k k 是否超标等等. 常见离散r.v.的分布 凡试验只有两个结果, 常用0 – 1 分布描述, 如产品是否合格、人 口性别统计、系统是否正常、电力消耗 X = xk 1 0 Pk p 1 - p 0 < p < 1 应用 场合 或

(2)二项分布 n重Bernoulli试验中,X是事件A在n次试 验中发生的次数,P(4)=p,若 Pn(k)=P(X=k)=Cp(I-p)”-k,k=0,L…,n 则称X服从参数为n,p的二项分布,记作 X~B(n,p) 0-1分布是n=1的二项分布
(2) 二项分布 n 重Bernoulli 试验中, X 是事件A 在 n 次试 验中发生的次数 , P (A) = p ,若 P k P X k C p p k n k k n k n n ( ) = ( = ) = (1− ) , = 0,1, , − 则称 X 服从参数为n, p 的二项分布,记作 X ~ B(n, p) 0–1 分布是 n = 1 的二项分布
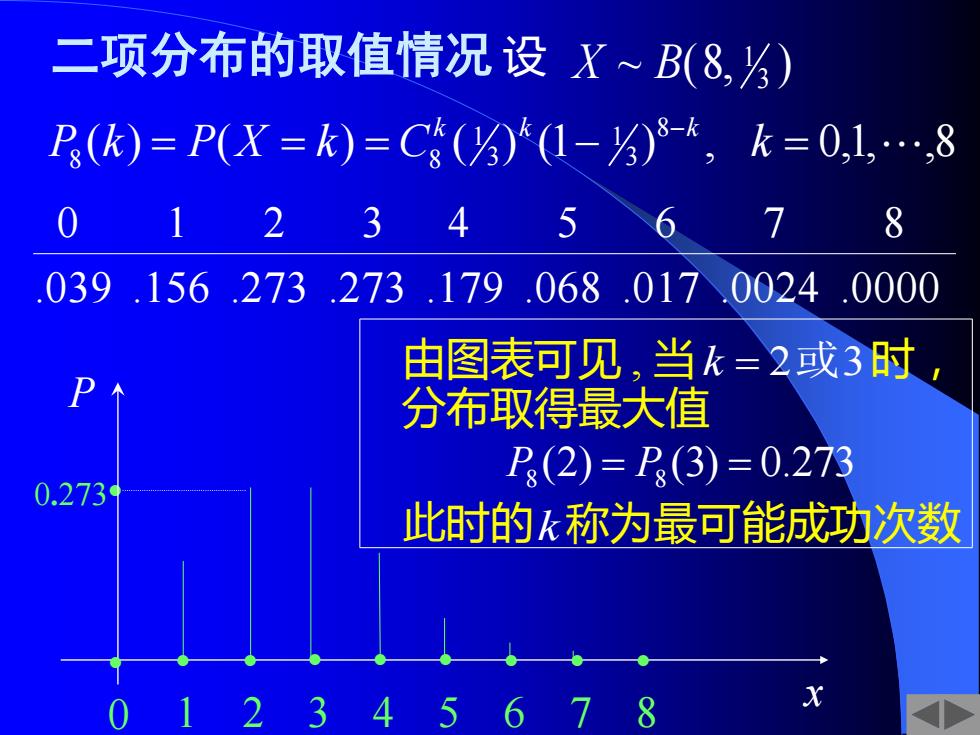
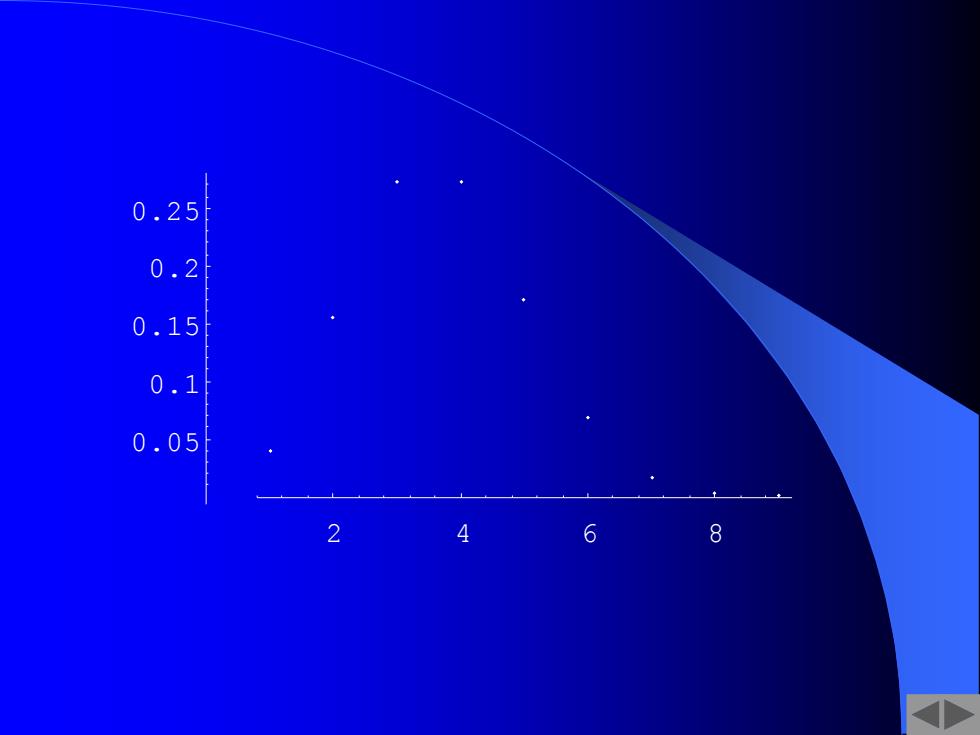
二项分布的取值情况设X~B(8,⅓) P(k)=P(X=)=C(⅓)(I-⅓)8-,k=0,1…,8 0 123 4 5 8 039.156.273.273.179.068.017.0024.0000 由图表可见,当k=2或3时, 分布取得最大值 P(2)=P(3)=0.273 0.273 此时的k称为最可能成功次数 012345678
二项分布的取值情况 设 ~ (8, ) 3 X B 1 .039 .156 .273 .273 .179 .068 .017 .0024 .0000 0 1 2 3 4 5 6 7 8 ( ) ( ) ( ) (1 ) , 0,1, ,8 8 3 1 3 1 P8 k = P X = k = C8 k k − −k k = 0.273• 由图表可见 , 当 k = 2或3 时, 分布取得最大值 P8 (2) = P8 (3) = 0.273 此时的 k 称为最可能成功次数 x P • 0 • 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8
0.25 0.2 0.15 0.1 0.05 2 4 6
2 4 6 8 0.05 0.1 0.15 0.2 0.25

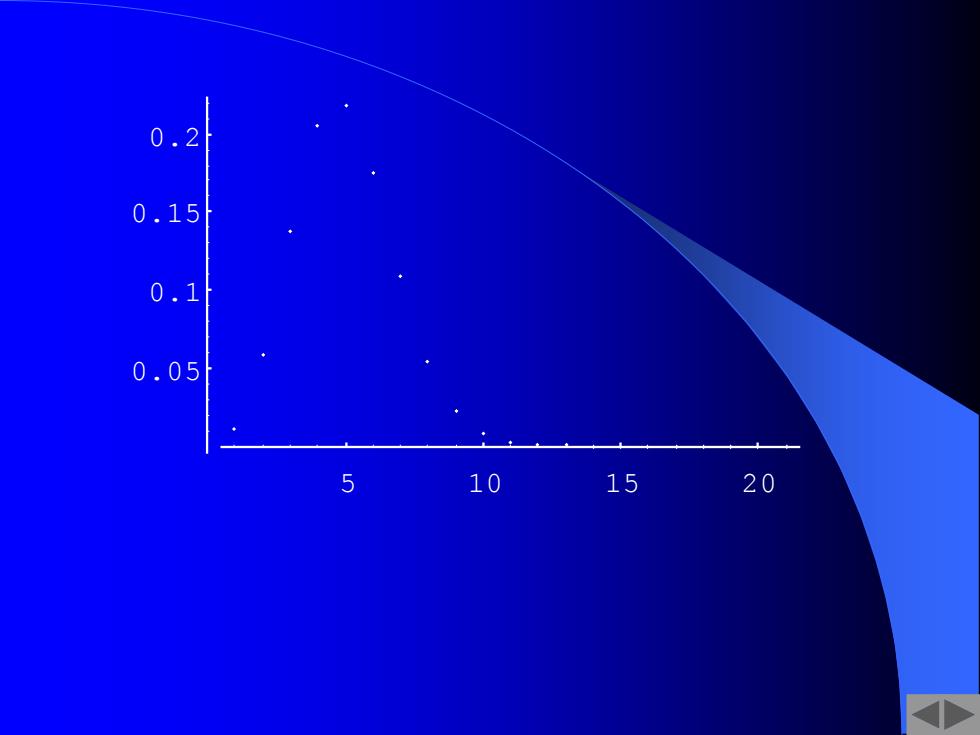
设X~B(20,0.2 01234567 891011~20 01.06.14.21.22.18.11.06.02.01.002<.001 由图表可见,当k=4时 0.22 分布取得最大值 P2(4)=0.22 012345678910 20
设 X ~ B(20,0.2) .01 .06 .14 .21 .22 .18 .11 .06 .02 .01 .002 < .001 0 1 2 3 4 5 6 7 8 9 10 11 ~ 20 • • x P • • • • • 1 • 3 • 5 • 7 • 9 • • • • 0 • 2 • 4 • 6 • 8 • 10 • 20 由图表可见 , 当 k = 4 时, 分布取得最大值 P20 (4) = 0.22 0.22 •
0.2 0.15 0.1 0.05 5 10 15 20
5 1 0 1 5 2 0 0.05 0.1 0.15 0.2