
第八章假设检验
第八章 假设检验

8.1假设检验的基本概念 假设检验是统计学中一种基本的统计推断形 式,是样本推断总体的一种方法。其基本原 理是先对总体的特征作某种假设,依据统计 原理,通过抽样做出对此假设应该拒绝还是 接受的推断
8.1 假设检验的基本概念 假设检验是统计学中一种基本的统计推断形 式,是样本推断总体的一种方法。其基本原 理是先对总体的特征作某种假设,依据统计 原理,通过抽样做出对此假设应该拒绝还是 接受的推断

引例某厂生产的螺钉,按标准强度为68克/mm2, 而实际生产的螺钉强度X服从N(山,3.62). 若E(X)=4=68,则认为这批螺钉符合要 求,否则认为不符合要求.为此提出如下假设: H0:4=68 称为原假设或零假设 原假设的对立面: H1:4≠68 称为备选假设 现从该厂生产的螺钉中抽取容量为36的样本,其样 本均值为x=68.5,问原假设是否正确?
引例 某厂生产的螺钉,按标准强度为68克/mm2 , 而实际生产的螺钉强度 X 服从 N ( µ ,3.6 2 ). 若 E ( X ) = µ = 68, 则认为这批螺钉符合要 求,否则认为不符合要求.为此提出如下假设: H0 : µ = 68 称为原假设或零假设 原假设的对立面: H1 : µ ≠ 68 称为备选假设 现从该厂生产的螺钉中抽取容量为 36 的样本,其样 本均值为 x = 68.5 ,问原假设是否正确?

假设检验就是要根据样本数据,利用概率的方法 对原假设Ho的合理性作出判断。若检验出Ho合 理,则接受H0;若“从概率上找到明显的证据” 说明Ho不合理,则拒绝Ho,进而接受H1。 如果总体的分布类型已知,仅是某些参数未知, 只要对未知参数作出假设,进行统计推断,这 种仅涉及到总体未知参数的检验称为参数假设 检验
假设检验就是要根据样本数据,利用概率的方法 对原假设𝑯𝑯𝟎𝟎的合理性作出判断。若检验出𝑯𝑯𝟎𝟎合 理,则接受 𝑯𝑯𝟎𝟎; 若“从概率上找到明显的证据” 说明𝑯𝑯𝟎𝟎不合理,则拒绝𝑯𝑯𝟎𝟎,进而接受𝑯𝑯𝟏𝟏。 如果总体的分布类型已知,仅是某些参数未知, 只要对未知参数作出假设,进行统计推断,这 种仅涉及到总体未知参数的检验称为参数假设 检验

进行假设检验的原则为实际推断原理: 小概率事件(概率≤0.05或0.01)在一次 试验中几乎是不可能发生的. 进行假设检验的思想: 概率意义下的反证法思想
进行假设检验的原则为实际推断原理: 小概率事件(概率 ≤ 0.05 或 0.01) 在一次 试验中几乎是不可能发生的. 进行假设检验的思想: 概率意义下的反证法思想

分析与解:若原假设正确,则 X~N(68, .62 36 因而E(X)=68,即X偏离68不应该太远,偏离较远 是小概率事件, 由于 X-68 3.6 N(0,) 6 故 X-68 取较大值是小概率事件 3.6 6
分析与解:若原假设正确, 则 ) 36 3.6 ~ (68 , 2 X N 故 68 3.6 6 X − 取较大值是小概率事件 因而 E(X ) = 68,即 X 偏离68不应该太远, 是小概率事件, 偏离较远 由于 ~ (0,1) 6 3.6 68 N X −

规定α为小概率事件的概率大小,通常取 a=0.05,0.01,. 因此,可以确定一个常数c,使得 8-68 D >C 6 例如, 取=0.05, 则 c=2g=20.025=1.96
规定α为小概率事件的概率大小,通常取 α = 0.05, 0.01,… 68 3.6 6 X P c α − > = 例如, 取 α = 0.05 , 则 1.96 c = z α 2 = z0.025 = 因此,可以确定一个常数 c ,使得

灭-68 由 >1.96 x>69.18或 3.6 <66.824 6 称又的取值区间 (66.824,69.18) 为检验的接受域(实际上没理由拒绝), 而区间 (-0,66.824)与(69.18,+0) 为检验的拒绝域 现x=68.5落入接受域,则接受原假设巧:4=68
1.96 6 3.6 68 > X − 由 称 的取值区间 (66.824 , 69.18) X 为检验的接受域 (实际上没理由拒绝), 现 x = 68.5 落入接受域, 则接受原假设 H0:µ = 68 66.824 69.18 X X 或 ( −∞ ,66.824 ) 与 ( 69.18 , +∞ ) 为检验的拒绝域 而区间

由引例可见,在给定α的前提下,接受还 是拒绝原假设完全取决于样本值,因此所作检验 可能导致以下两类错误的产生: 第一类错误 弃真错误 第二类错误 取伪错误
由引例可见,在给定 α 的前提下,接受还 是拒绝原假设完全取决于样本值, 因此所作检验 可能导致以下两类错误的产生: 第一类错误 弃真错误 第二类错误 取伪错误
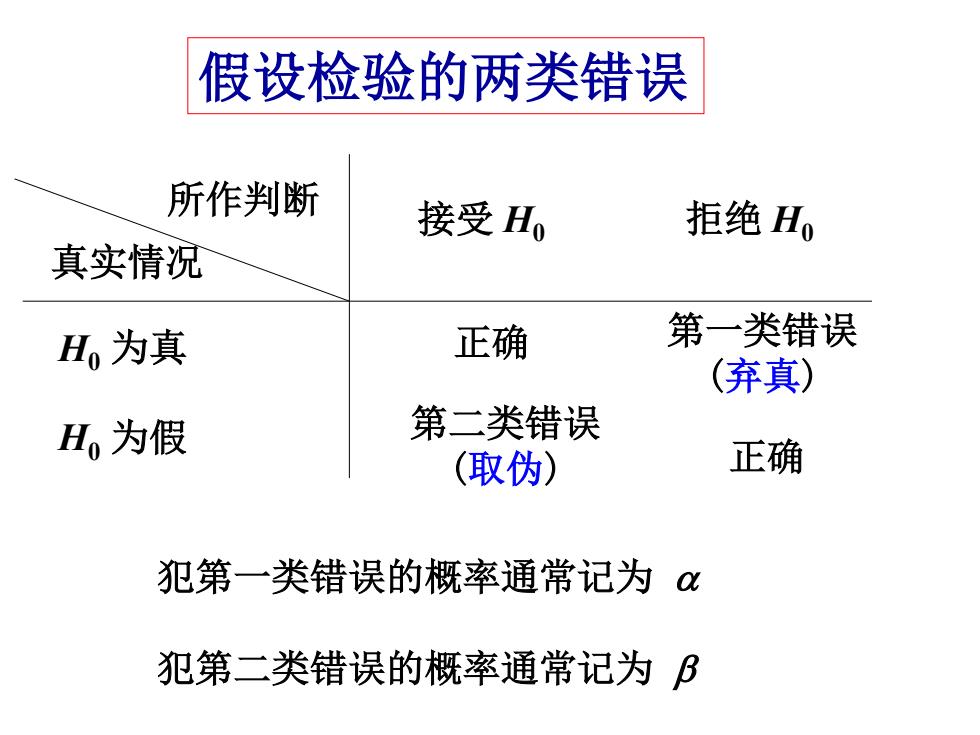
假设检验的两类错误 所作判断 接受Ho 拒绝H 真实情况 Hn为真 正确 第一类错误 (弃真) H,为假 第二类错误 (取伪) 正确 犯第一类错误的概率通常记为α 犯第二类错误的概率通常记为B
H0 为真 H0 为假 真实情况 所作判断 接受 H0 拒绝 H0 正确 正确 第一类错误 (弃真) 第二类错误 (取伪) 假设检验的两类错误 犯第一类错误的概率通常记为 α 犯第二类错误的概率通常记为 β