
3.3随机变量的独立性 将事件独立性推广到随机变量 定义 设(XY)为二维随机变量若对任何 实数飞,y都有 P(X≤x,Y≤y)=P(X≤x)P(Y≤y) 则称随机变量X和Y相互独立
3.3 随机变量的独立性 —— 将事件独立性推广到随机变量 设(X,Y )为二维随机变量若对任何 P(X ≤ x,Y ≤ y) = P(X ≤ x)P(Y ≤ y) 则称随机变量 X 和Y 相互独立 实数 x, y 都有 定义

由定义知 (X,Y)相互独立 →F(x,y)=Fx(x)Fy(y) Vaa,Y>c)=P(X>a)P(Y>c)
由定义知 ( X, Y ) 相互独立 F(x, y) F (x)F ( y) = X Y ( ) ( ) ( , ) , P a X b P c Y d P a X b c Y d a b c d = > = > > ∀ ∈

离散型 X与Y独立→对一切i,i有 Pi =PiP.i P(X=xY=y)=P(X=x)P(Y=Y) 连续型 X与Y独立→对任何x,y有 f(x,y)=fx(x)f(y)(ae.) 二维随机变量(X,Y)相互独立, 则边缘分布完全确定联合分布
X与Y 独立 ( , ) ( ) ( ) i j i j 即 P X = x Y = y = P X = x P Y = y ij i j p p p = • • 连续型 f (x, y) f (x) f ( y) = X Y 二维随机变量 ( X, Y ) 相互独立, 则边缘分布完全确定联合分布 离散型 对一切 i , j 有 X与Y 独立 对任何 x ,y 有 (a.e.)

二维连续随机变量(X,Y)相互独立 →fx(x)=fxy()(f,()>0) f()=fx(vx)(fx(x)>0) 随机变量的函数 若X与Y相互独立,gx)与h(y)是两 个确定函数,则g)与h()也相互 独立
二维连续随机变量 ( X,Y ) 相互独立 f (x) = f (x y) ( f ( y) > 0) X X Y Y f ( y) = f ( y x) ( f (x) > 0) Y Y X X 随机变量的函数 若X与Y相互独立,g(x)与h(y)是两 个确定函数,则g(X)与h(Y)也相互 独立

由上结论知 若X,Y为相互独立的随机变量 则aX+b.cY+d也相互独立: X2,Y2也相互独立; 随机变量相互独立的概念 可以推广到n维随机变量 若 P(X1≤x,X2≤x,,Xn≤x) =P(X1≤x)P(X2≤x2)…P(Xn≤xn) 则称X,X2,,Xn相互独立
若 X ,Y 为相互独立的随机变量 则aX + b, cY + d 也相互独立; X 2, Y 2 也相互独立; 随机变量相互独立的概念 可以推广到 n 维随机变量 ( ) ( ) ( ) 1 1 2 2 n n = P X ≤ x P X ≤ x P X ≤ x ( , , , ) 1 1 2 2 n n 若 P X ≤ x X ≤ x X ≤ x 则称 X 1, X 2 , , Xn 相互独立 由上结论知
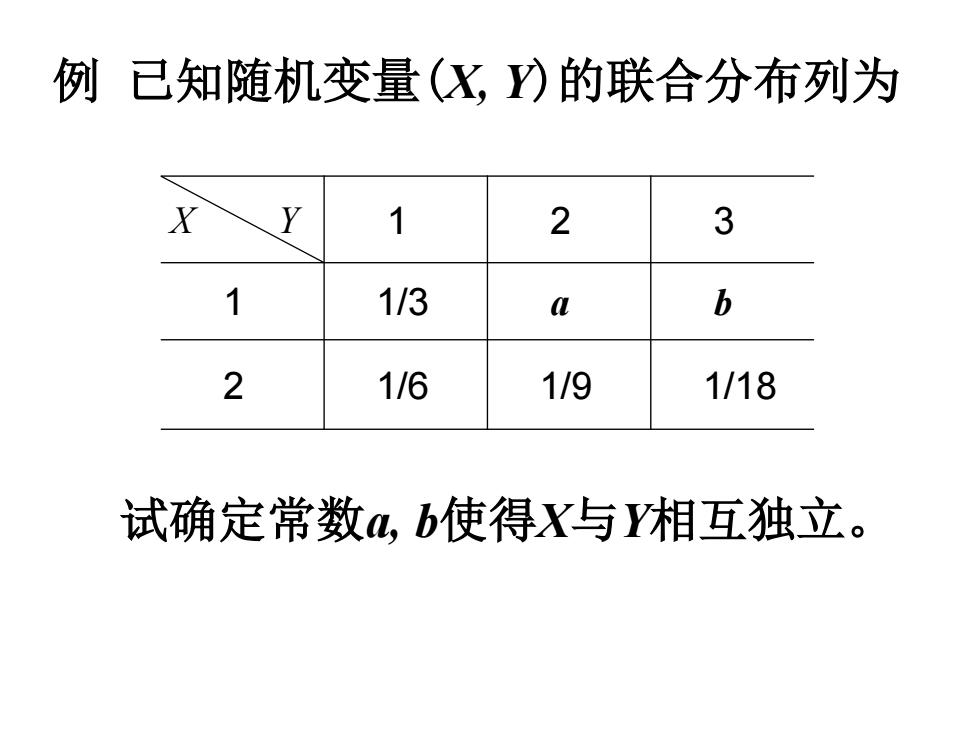
例已知随机变量(X,)的联合分布列为 1 2 3 1/3 L b 2 1/6 1/9 1/18 试确定常数a,b使得X与Y相互独立
例 已知随机变量(X, Y)的联合分布列为 X Y 1 2 3 1 1/3 a b 2 1/6 1/9 1/18 试确定常数a, b使得X与Y相互独立

例(Craps掷骰子游戏)某游戏规定:同时掷两枚骰 子,直到首次出现,点数和为4或者点数和为7时游戏停 止。如果停止时出现,点数和为4,则甲赢;如果停止时 出现点数和为7,则乙赢。令 X= 甲赢; 0, 乙赢, Y="游戏停止时掷骰子的总次数” 问题:随机变量X,Y是否相互独立?
例 (Craps掷骰子游戏)某游戏规定:同时掷两枚骰 子,直到首次出现点数和为4或者点数和为7时游戏停 止。如果停止时出现点数和为4,则甲赢;如果停止时 出现点数和为7,则乙赢。令 1 = 0, X , 甲赢; 乙赢, Y = " " 游戏停止时掷骰子的总次数 问题:随机变量 X Y, 是否相互独立?

解:掷两枚骰子,每次出现点数和为4的概率为 3=1 3612 点数和为7的概率 61 366 既不是4也不是7的概率为1-1-} 126 并且每次都是投掷两枚骰子,各次骰子出现的结 果相互独立,故 P(X=1,Y=n) =P(第n次点数和为4,前n-1次点数和不是4也不是7) 立日
解:掷两枚骰子,每次出现点数和为4的概率为 3 1 = 36 12 点数和为7的概率 6 1 = 36 6 既不是4也不是7的概率为 1 1 1 12 6 − − 并且每次都是投掷两枚骰子,各次骰子出现的结 果相互独立,故 ( 1, ) ( 4, -1 4 7 ) PX Y n P n n = = = 第 次点数和为 前 次点数和不是 也不是 1 1 11 1 3 1 = 1 12 6 12 4 12 n n − − −− ⋅= ⋅

P(X=0,Y=n) =P(第n次点数和为7,前n-1次点数和不是4也不是7) =-名(8 从而 x=-8b时 =0-6 P(Y=n)= 1 n=1,2, 根据定义知X,Y是相互独立的
( 0, ) ( 7, -1 4 7 ) PX Y n P n n = = = 第 次点数和为 前 次点数和不是 也不是 1 1 11 1 3 1 = 1 12 6 6 4 6 n n − − − − ⋅= ⋅ 从而 1 1 3 11 ( 1) = 4 12 3 n n P X − ∞ = = = ⋅ ∑ 1 1 3 12 ( 0) 4 63 n n P X − ∞ = = = ⋅= ∑ 1 3 1 ( ) 1, 2, 4 4 n PY n n − == ⋅ = , 根据定义知 X Y, 是相互独立的

命题(X,Y)~N(4,o4,o:p)相互独立 >=0 证→对任何x,y有 1 0102 2π0,02V1-p2 14 1 _0y-2)2 e 2o e 2π01 √2π02 取x=41,y=42
ρ = 0 2 2 2 2 2 1 2 1 2 2 2 2 1 2 1 2 2 1 2 1 2 2 ( ) 2 2 ( ) 1 ( )( ) ( ) 2 ( ) 2(1 ) 1 2 1 2 2 1 2 1 2 1 1 σ µ σ µ σ µ σ σ µ µ ρ σ µ ρ πσ πσ πσ σ ρ − − − − − + − − − − − − = − x y x x y y e e e 证 对任何 x,y 有 1 2 取 x = µ , y = µ ( , ) ~ ( , ; , ; ) 2 2 2 2 命题 X Y N µ1 σ 1 µ σ ρ 相互独立