
第之章行利或 第一节二阶、三阶行列式 一、二阶行列式的引入 二、三阶行列式 三、小节、思考题
第二章 行列式 第一节 二阶、三阶行列式 一、二阶行列式的引入 二、三阶行列式 三、小节、思考题

一、二阶行列式的引入 用消元法解二元线性方程组 a1x+a12x2=b,() 21x1+422x2=b2. (2) ()×a2:a11421t42422r2=b22, (2)×a12:42421xt012422=b2412 两式相减消去x2,得 上页
用消元法解二元线性方程组 + = + = . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b (1) (2) (1) : a22 , a11a22 x1 + a12a22 x2 = b1a22 (2) : a12 , a12a21x1 + a12a22 x2 = b2a12 两式相减消去 x2,得 一、二阶行列式的引入

(a11022-412421)x1=b422-412b2; 类似地,消去x,得 (a11422-412421)x2=a1b2-b1421y 当4112-a12421≠0时,方程组的解为 0哈, (3) 411022-0122 由方程组的四个系数确定. 回
; (a11a22 − a12a21)x1 = b1a22 − a12b2 类似地,消去x1,得 , (a11a22 − a12a21)x2 = a11b2 − b1a21 当 a11a22 − a12a21 0时, 方程组的解为 , 11 22 12 21 1 22 12 2 1 a a a a b a a b x − − = . (3) 11 22 12 21 11 2 1 21 2 a a a a a b b a x − − = 由方程组的四个系数确定

定义 由四个数排成二行二列(横排称行、竖排 称列)的矩阵: 1112 21L22 (4) 称表达式011422-a122为矩阵(4)所确定的二阶 行列式,并记作 011012 (5) 21 L22 页
由四个数排成二行二列(横排称行、竖排 称列)的矩阵: (4) 21 22 11 12 a a a a 定义 (5) 4 2 1 2 2 1 1 1 2 1 1 2 2 1 2 2 1 a a a a a a a a 行列式,并记作 称表达式 − 为矩阵( )所确定的二阶

二阶行列式的计算一对角线法则 主对角线 12 =%1122-012421 副对角线 22 对于二元线性方程组 若记 系数行列式 22 上页 区回
11 a 12 a a12 a22 主对角线 副对角线 对角线法则 = a11a22 . − a12a21 二阶行列式的计算 若记 , 21 22 11 12 a a a a D = + = + = . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 对于二元线性方程组 系数行列式

4+a12x2 21x1+22X2 D 411 D 上页 下页 区回
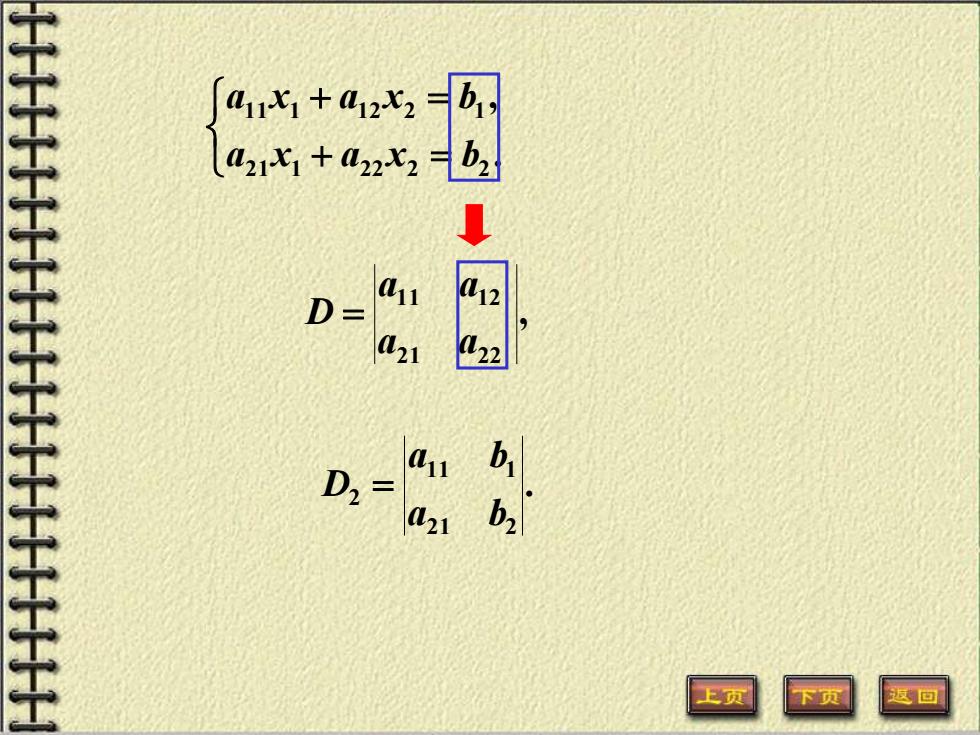
+ = + = . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b , 21 22 11 12 a a a a D = , 2 22 1 12 1 b a b a D =
D 11 上页 返回
+ = + = . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b , 21 22 11 12 a a a a D = . 21 2 11 1 2 a b a b D =

则二元线性方程组的解为 012 D b2 422 X1= D a11 12 x2= 421 D 41u 12 21 L22 21 L22 注意 分母都为原方程组的系数行列式 上页
则二元线性方程组的解为 , 21 22 11 12 2 22 1 12 1 1 a a a a b a b a D D x = = 注意 分母都为原方程组的系数行列式. . 21 22 11 12 21 2 11 1 2 2 a a a a a b a b D D x = =

二、三阶行列式 定义 设有9个数排成3行3列的矩阵 au L12 13 21 L22 L23 (6) 记 l31 032 33 i 12 13 (7) 22 l23 =4112233+41202331+41321432 31 32 L33 -011023032-4122133-%132231, (7)式称为矩阵(6)所确定的三阶行列式, 上页 下页 区回
二、三阶行列式 定义 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 (6) 9 3 3 a a a a a a a a a 设有 个数排成 行 列的矩阵 记 1 1 2 3 3 2 1 2 2 1 3 3 1 3 2 2 3 1, 1 1 2 2 3 3 1 2 2 3 3 1 1 3 2 1 3 2 (7) a a a a a a a a a a a a a a a a a a − − − = + + 31 32 33 21 22 23 11 12 13 a a a a a a a a a (7)式称为矩阵(6)所确定的三阶行列式
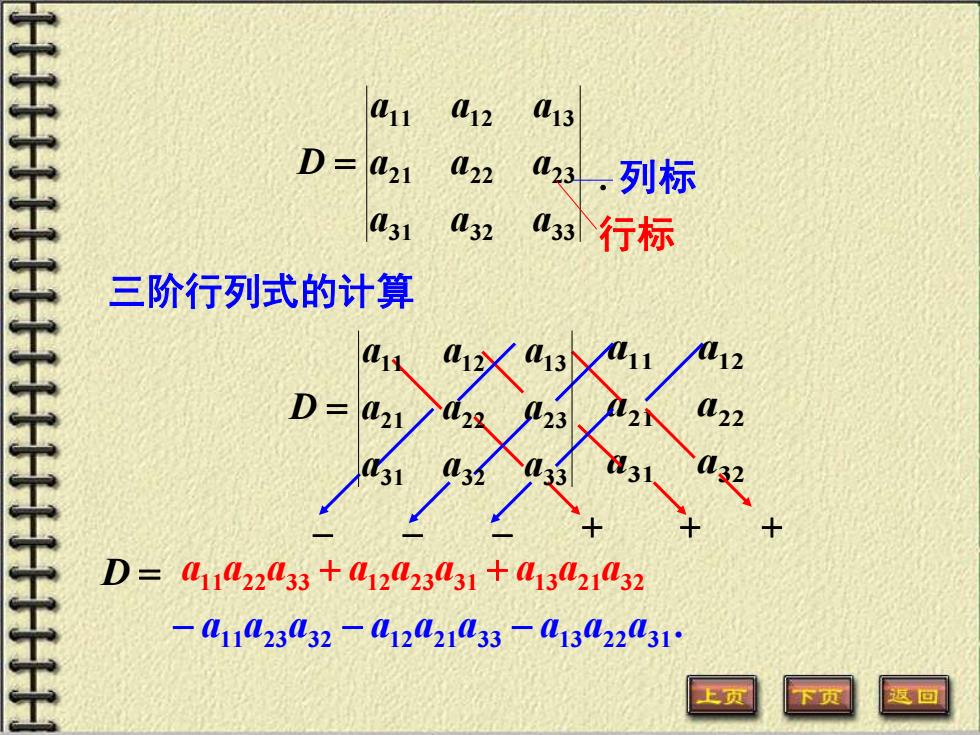
11 12 L13 D= M21 L22 L23 一列标 31 L32 33 行标 三阶行列式的计算 D=411422033+41223431+41342132 -41023032-41202133-132231° 上页
31 32 21 22 11 12 a a a a a a − − − + + + . − a11a23a32 − a12a21a33 − a13a22a31 三阶行列式的计算 D = a11a22a33 + a12a23a31 + a13a21a32 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = .列标 行标 31 32 33 21 22 23 11 12 13 a a a a a a a a a D =