
Ch4 南餐空间 第一节 向量组的线性相关 与线性无关 > 一、向量、向量组与矩阵 二、线性相关性的概念 三、线性相关性的判定 四、向量组的线性相关性质 五、线性表示、线性相关以及 线性无关三者的关系 六、小节、思考题
Ch4 向量空间 第一节 向量组的线性相关 与线性无关 一、向量、向量组与矩阵 二、线性相关性的概念 三、线性相关性的判定 六、小节、思考题 四、向量组的线性相关性质 线性无关三者的关系 五、线性表示、线性相关以及

一、向量、向量组与矩阵 n维向量写成一行,称为行向量,也就是行 矩阵,通常用a,b,a,B等表示,如: a'=(a1,2,,n) n维向量写成一列,称为列向量,也就是列 矩阵,通常用4,b,a,B等表示,如: d=
( , , , ) 1 2 n T a = a a a = an a a a 2 1 一、向量、向量组与矩阵 维向量写成一行,称为行向量,也就是行 矩阵,通常用 等表示,如: T T T T a ,b , , n 维向量写成一列,称为列向量,也就是列 矩阵,通常用 a,b,, 等表示,如: n
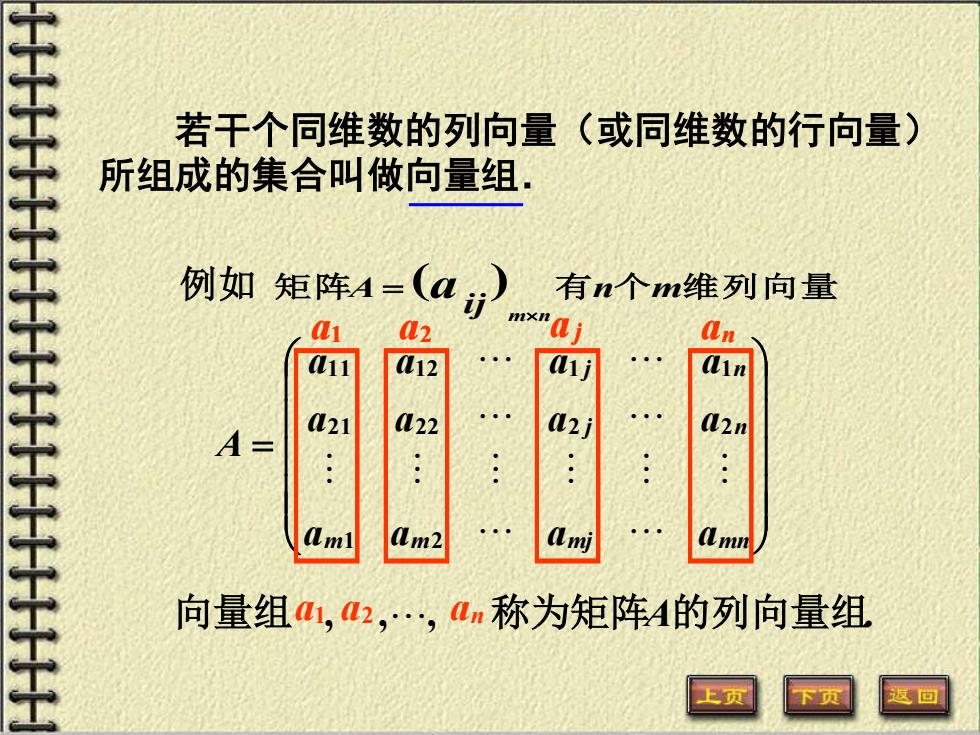
若干个同维数的列向量(或同维数的行向量) 所组成的集合叫做向量组. 例如矩阵4=(a)有n个m维列向量 L21 L22 4- Lm 向量组1,42,,4m称为矩阵4的列向量组 回
若干个同维数的列向量(或同维数的行向量) 所组成的集合叫做向量组. 例如 矩 阵A ai j 有n个m维列向量 m n ( ) = = a a a a a a a a a a a a A m m mj mn j n j n 1 2 2 1 2 2 2 2 1 1 1 2 1 1 a1 向量组 a1, a2 , , an 称为矩阵A的列向量组. a1 a2 a j an

类似地,矩阵A=(ai)又有m个n维行向量 L11 L12 a l21 L22 A2n az A三 ai Qi2 Ain a Am2 a 向量组a{,aZ,.,am称为矩阵A的行向量组
类似地 矩 阵A ai j 又 有m个n维行向量 m n , ( ) = = a a a a a a a a a a a a A m m mn i i in n n 1 2 1 2 21 22 2 11 12 1 T 1 T 2 T i T m T 1 T 2 T i T m 向量组 , , …, 称为矩阵A的行向量组. T 1 T 2 T m

反之,由有限个向量所组成的向量组可以构 成一个矩阵. m个n维列向量所组成的向量组a1,c2,,am, 构成一个m×n矩阵 A=(C1,a2,,am) m个n维行向量所组成 的向量组B,B2,BnmT, B= B." 构成一个m×n矩阵 这回
反之,由有限个向量所组成的向量组可以构 成一个矩阵. 构成一个 矩阵 个 维列向量所组成的向量组 m n m n m , , , , 1 2 构成一个 矩阵 的向量组 个 维行向量所组成 m n m n T m T T , , , 1 2 = T m T T B 2 1 ( , , , ) A = 1 2 m
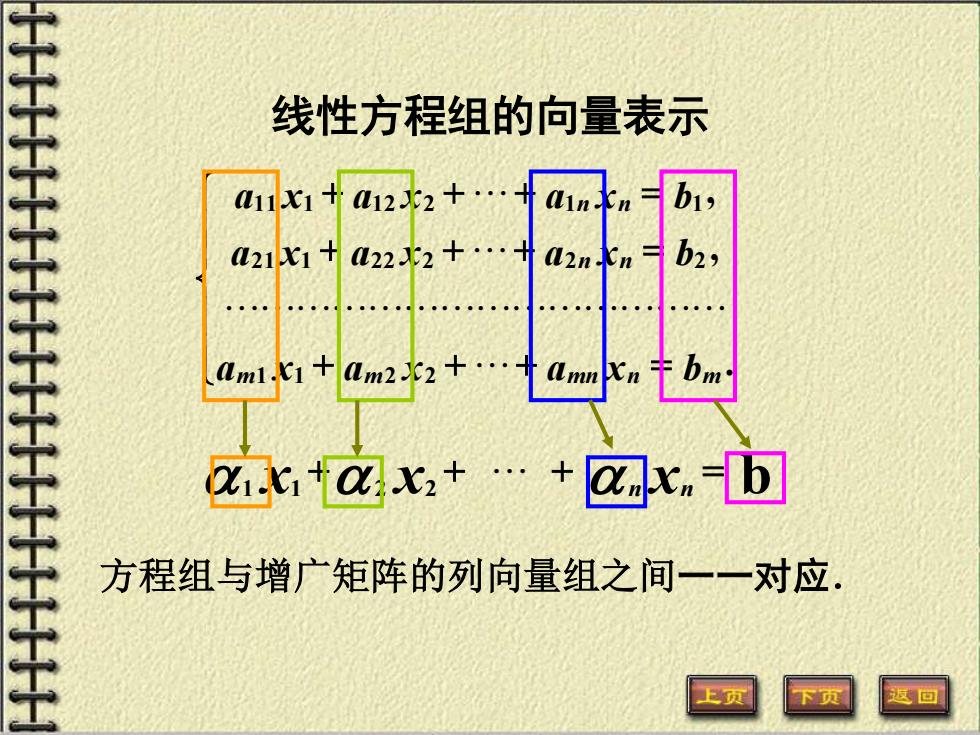
线性方程组的向量表示 x1+a122+ 211十a222+… aml1+0m22+… 00 kta☑x+.+☑xb 方程组与增广矩阵的列向量组之间一一对应 页
1 x1 +2 x2 + + n xn = b 线性方程组的向量表示 + + + = + + + = + + + = . , , 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 a x a x a x b a x a x a x b a x a x a x b m m mn n m n n n n 方程组与增广矩阵的列向量组之间一一对应.

定义1给定向量组4:a1,a2,,am,对于任何一 组实数k1,k2y,km向量 k11+k2a2+…+kmam 称为向量组的一个线性组合k,k2,,km称为这 个线性组合的系数 上页 返回
组实数 , , , 给定向量组 ,对于任何一 m m k k k A , : , , , 1 2 1 2 定义1 . , 1 2 个线性组合的系数 称为向量组的一个 , k ,k , km称为这 向 量 k11 + k2 2 ++ km m 线性组合

给定向量组4:a1,a2,,am和向量b,如果存在 一组数11,2,,入m,使 b=1a1+2a2+…2mam 则向量是向量组4的线性组合,; 这时称向量b能 由向量组A线性表示 即线性方程组 X1a1+X2a2+…+Xmam=b 有解.也就是方程组Ar=b有解, 其中,A=[a,a2,an]
b = 11 + 2 2 + m m 一组数 , , , 使 给定向量组 和向量 如果存在 m A m b , : , , , , 1 2 1 2 . 1 1 2 2 有解 即线性方程组 x + x + + xm m = b 则向量b是向量组A的线性组合,这时称 向量 能 由向量组 线性表示. b A 也就是方程组 Ax = b 有解, , , . 其中,A = 1 2 n

定理1向量b能由向量组4线性表示的充分必要 条件是矩阵A=(a,a2,…,am)的秩等于矩阵 B=(a1,a2,…,am,b)的秩 [2 例:向量b--3即可由向量组g1= 002= 0 o 010 [0 03= 0线性表示,且为:b=2a1-3a2+0a3 b
( , , ) . ( , ) 1 2 1 2 , , 的 秩 条件是矩阵 , , 的秩等于矩阵 向 量 能由向量组 线性表示的充分必要 B b A b A m m = = 定理1 例:向量 即可由向量组 , , = = = − 0 1 0 0 0 1 0 3 2 b 1 2 3 2 1 3 2 0 3 1 0 0 = − + = 线性表示,且为:b

因为 [1002 B=4,b1=[a1,a2,a3,b]=01 即r(A)=r(B)) 定义2设有两个向量组 A:a1,a2,,amB:B,B2,,B 若B组中的每个向量都能由向量组A线性表示,则 称向量组能由向量组线性表示.若向量组A与向 量组B能相互线性表示,则称这两个向量组等价. 上页
. : , , , : , , , . 1 2 1 2 量 组 能相互线性表示,则称这两个 称 若向量组 与 向 若 组中的每个向量都能由向量组 线性表示,则 及 设有两个向量组 B A B A A m B s 向量组 能由向量组 线性表示 向量组等价. B A 定义2 即r(A) = r(B).) = = = − 0 0 1 0 0 1 0 3 1 0 0 2 [ , ] , , , B A b 1 2 3 b (因为