5.2中心极限定理 引例 X,X,.., Xm相互 独立,均服从参数为 1.0 1.4 12 2的指数分布,令 0. k=1 0.8 0.7 n=2 n=5 >n=2 n=15 n=20 0.5 -n=30 30.4 n=5 n=15 0.3 n=20 n=30 2. 0 10 15 20 25 30
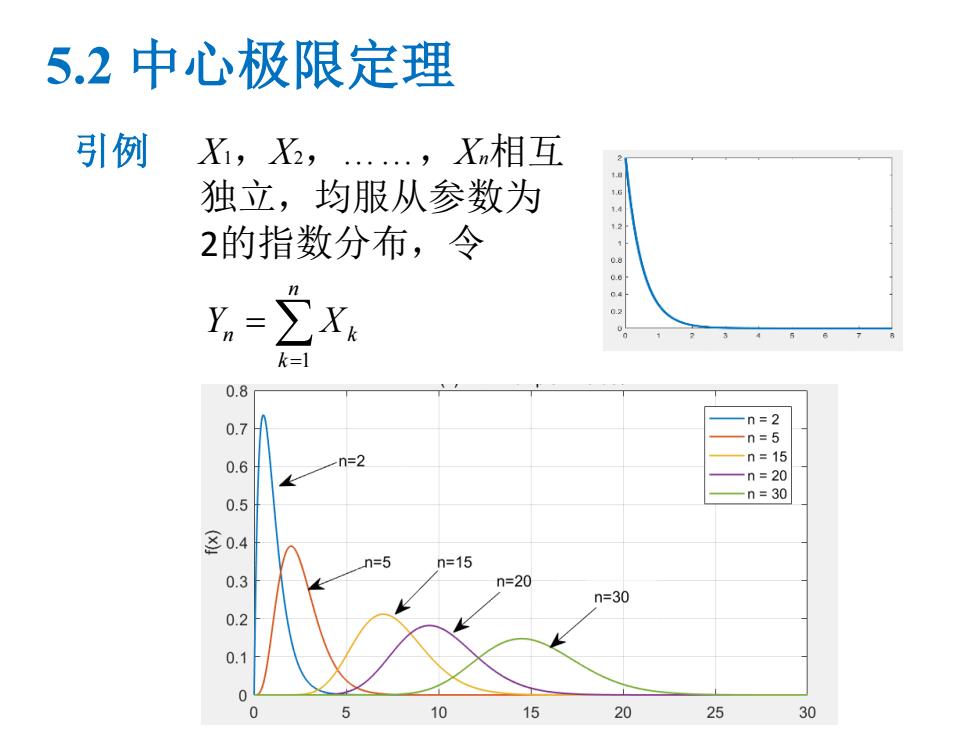
5.2 中心极限定理 引例 X1,X2,……,Xn相互 独立,均服从参数为 2的指数分布,令 1 n n k k Y X = = ∑
n=30 n=2 n=5 n=50 4 n=15 n=20 n=30 83 n=50 0.5 1.5 =12x n k=1 主要分布区域越来越集中,其中心位 置越来越接近 EZ)=}=0,5
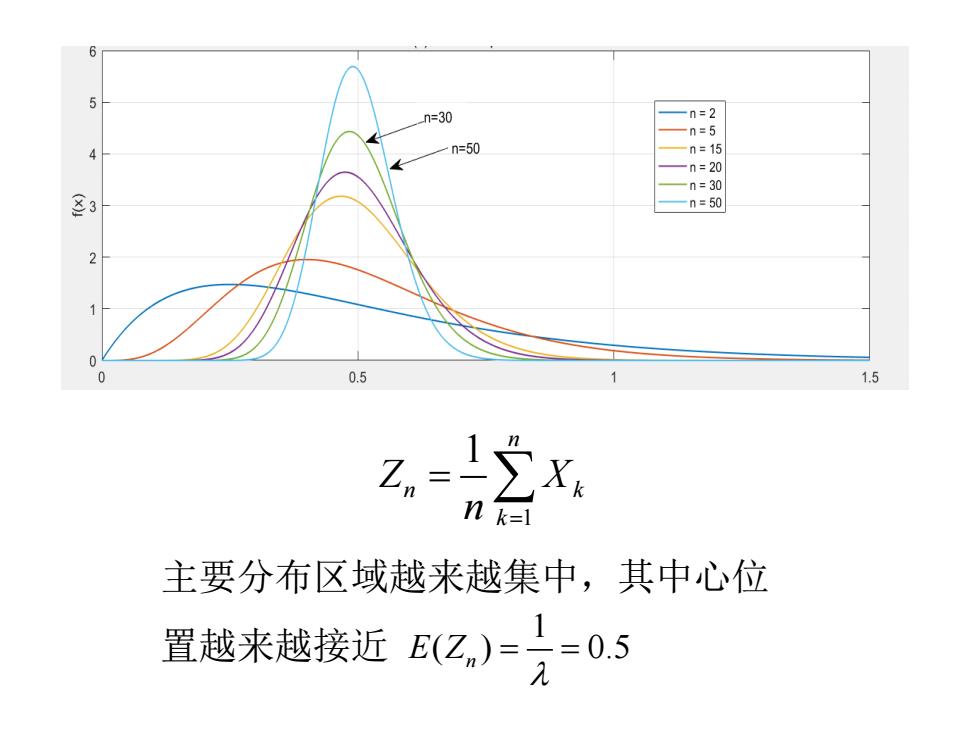
1 1 n n k k Z X n = = ∑ 主要分布区域越来越集中,其中心位 置越来越接近 1 ( ) 0.5 E Z n λ = =

定理1 独立同分布的中心极限定理 设随机变量序列X1,X2,…,Xn,…相互 独立,服从同一分布,且有期望和方差: E(X&)=4,D(Xk)=o2>0,k=1,2,… 则对于任意实数x, ∑X-nu lim P k= n->oc
定理1 独立同分布的中心极限定理 设随机变量序列 X1, X2 ,, X n , 相互 独立,服从同一分布,且有期望和方差: E(Xk ) = µ , D(Xk ) =σ2 > 0 , k =1,2, 则对于任意实数 x , ∫ ∑ −∞ − = →∞ = ≤ − x t n k k n x e dt n X n P 1 2 2 2 1 lim π σ µ

注:记 no 则Ym为∑X的标准化随机变量. k= limP(Yn≤x)=Φ(x) 即n足够大时,Y,的分布函数近似于标准正态 随机变量的分布函数 y,(0,1) 近似 三X.=no.+近似服从N0wLo)
注: 则 Y n 为∑= n k Xk 1 的标准化随机变量. limP(Y x) (x) n n ≤ =Φ →∞ 即 n 足够大时,Y n 的分布函数近似于标准正态 随机变量的分布函数 σ µ n X n Y n k k n − = ∑=1 记 Y ~ N(0,1) n 近似 ∑= n k Xk 1 = nσY n + nµ ( , ) 2 近似服从 N nµ nσ

定理2 德莫佛一 拉普拉斯中心极限定理 (DeMoivre-Laplace 设Yn~B(n,p),0<p<1,n=1,2,. 则对任一实数x,有 小 lim P 2dt 即对任意的a<b, Ym~N(np,np(1-p)(近似)
定理2 德莫佛 — 拉普拉斯中心极限定理 (DeMoivre-Laplace ) 设 Y n ~ B( n , p) , 0 < p < 1, n = 1,2,… 则对任一实数 x,有 ∫−∞ − →∞ = ≤ − − x t n n x e dt np p Y np P 2 2 2 1 (1 ) lim π 即对任意的 a < b, ∫ − →∞ = ≤ − − < b a t n n b e dt np p Y np P a 2 2 2 1 (1 ) lim π Y n ~ N (np , np(1-p)) (近似)

注1n较小时,例n100,p<0.1时 用正态分布近似代替.即 Pa%s器-号 _(k-p)2 P(=k)≈。 ,2pg √2πpq
注1 n 较小时,例 n 100 , p < 0.1 时 用正态分布近似代替.即 ( )( )( ) n b np a np Pa b npq npq η − − < ≤ ≈Φ −Φ 2 ( ) 1 2 ( ) 2 k np npq Pk e n npq η π − − = ≈

例某射手射靶,得十分的概率为0.5,得九分的概率为 0.3,得八分的概率0.1得七分的概率为0.05,得六分的 概率为0.05.现独立的射击100次,用切比雪夫不等式和 中心极限定理估计总分介于900分与930分之间的概率。 解: 设X表示射击手第i次得分 Xk 10 9 8 Pk 0.5 0.3 0.1 0.05 0.05 E(X;)=9.15 E(X)=84.95D(X;)=1.2275 100 X=2X,E(X)=915D(X)=12.75 i=1 近似 X~N(915,122.75) P900<X<930)≈D 930-915 -Φ 900-915 ≈0.823 122.75 122.75
例 某射手射靶,得十分的概率为0.5,得九分的概率为 0.3,得八分的概率0.1得七分的概率为0.05,得六分的 概率为0.05.现独立的射击100次,用切比雪夫不等式和 中心极限定理估计总分介于900分与930分之间的概率。 解: 设 Xi 表示射击手第 i 次得分 Xk pk 10 9 8 7 6 0.5 0.3 0.1 0.05 0.05 ( ) 9.15 E Xi = 2 ( ) 84.95 E Xi = ( ) 1.2275 D Xi = 100 1 i i X X = = ∑ E X( ) 915 = D X( ) 122.75 = 930 915 900 915 (900 930) ( ) ( ) 0.823 122.75 122.75 P X − − < < ≈Φ −Φ ≈ X N ~ 915,122.75 ( ) 近似

例假设某教学楼每天大约有3000学生上课, 学生课间休息需要用饮水机水龙头接水喝, 经常出现同学排长队的现象,为此校学生会 特向后勤集团提议增设饮水机和水龙头总数。 假设后勤集团经过调查,发现每个学生在课 间一般有1%的时间要占用一个水龙头,现有 水龙头25个,现在后勤集团遇到的问题是: (1)未增装水龙头前,拥挤的概率是多少? (2)至少要装多少个水龙头,才能以95%以 上的概率保证不拥挤?
例 假设某教学楼每天大约有3000学生上课, 学生课间休息需要用饮水机水龙头接水喝, 经常出现同学排长队的现象,为此校学生会 特向后勤集团提议增设饮水机和水龙头总数。 假设后勤集团经过调查,发现每个学生在课 间一般有1%的时间要占用一个水龙头,现有 水龙头25个,现在后勤集团遇到的问题是: (1)未增装水龙头前,拥挤的概率是多少? (2)至少要装多少个水龙头,才能以95%以 上的概率保证不拥挤?

解:设同一时刻,3000个学生中占用水龙头的人数为 X,则 XB(3000,0.01) 由中心极限定理易知:X~N(30,29.7)(近似) (1)拥挤的概率 25-30 PX>25)=1-(297 0-(297-00.91761=082 (2)问题转化为求m,使得P(0≤X≤m)>0.95 0srsm)-w9)29)9}095 心929)0反查正态分布函数表,得 m-30 >1.645 √29.7 m>38.96 m≈39
解:设同一时刻,3000个学生中占用水龙头的人数为 X,则 X B ~ (3000,0.01) 由中心极限定理易知: X N ~ (30, 29.7)(近似) (1)拥挤的概率 25 30 5 ( 25) 1 ( ) ( ) (0.9176) 0.82 29.7 29.7 P X − > = −Φ =Φ =Φ = (2)问题转化为求m,使得 P Xm (0 ) 0.95 ≤≤ > 30 0 30 30 (0 ) 0.95 29.7 29.7 29.7 m m P Xm −− − ≤ ≤ =Φ −Φ ≈Φ > 0 30 0 29.7 − Φ ≈ 反查正态分布函数表,得 30 1.645 29.7 m − > m > 38.96 m ≈ 39

例某毕业生去到某保险公司应聘,面试官 给他的问题是:假设当地正在销售的一项意 外死亡保险,客户的数目大约1人万左右(按 1万人记),被保险人每年交200元保费,一 旦意外死亡发生,索赔金额为5万元,据经验 估计当地一年的意外死亡率为0.25%左右,请 问你能不能给出公司的获利情况?
例 某毕业生去到某保险公司应聘,面试官 给他的问题是:假设当地正在销售的一项意 外死亡保险,客户的数目大约1人万左右(按 1万人记),被保险人每年交200元保费,一 旦意外死亡发生,索赔金额为5万元,据经验 估计当地一年的意外死亡率为0.25%左右,请 问你能不能给出公司的获利情况?