
7.2点估计的评价标准 对于同一个未知参数,不同的方法得到 的估计量可能不同,于是提出问题 △应该选用哪一种估计量? △用什么标准来评价一个估计量的好坏? (I)无偏性(Unbiased Estimator) 常用 (2)有效性 标准 (3)一致性(consistency)
7.2 点估计的评价标准 对于同一个未知参数, 不同的方法得到 的估计量可能不同,于是提出问题 应该选用哪一种估计量? 用什么标准来评价一个估计量的好坏? 常用 标准 (1) 无偏性(Unbiased Estimator) (3) 一致性(consistency) (2) 有效性

○无偏性 定义设(X,X2,…,Xm)是总体X的样本 0=0(X1,X2,,Xm)是总体参数0的估计量 E(O)存在,且对于任意0∈⊙都有 E(0)=0 则称是0的无偏估计量
E(θ ˆ ) =θ 定义 设 ( , , , ) X1 X2 Xn 是总体X 的样本 ˆ (X1, X2 ,, Xn ) 是总体参数θ 的估计量 θ =θ 则称θ ˆ 是θ 的无偏估计量. ) 存在, ˆ E(θ 且对于任意θ ∈Θ都有 无偏性

例1设总体X的k阶矩4,=E(X存在 (X1,X2,…,Xn)是总体X的样本, 证明:不论X服从什么分布,4=之X 是山k的无偏估计量. 证 由于E(X)=4ki=1,2,…,n 因而 E(A)=E(2∑X)=∑E(X) n i=l 1 =-·nlk=lk n
( , , , ) X1 X2 Xn 是总体X 的样本, 证明: 不论 X 服从什么分布, ∑ = = n i k k Xi n A 1 1 是 µk 的无偏估计量. 证 ∑ ∑ = = = = n i k i n i k k i E X n X n E A E 1 1 ( ) 1 ) 1 ( ) ( 例1 设总体X 的 k 阶矩 ( ) k µk = E X 存在 由于E(Xi k ) = µk i = 1,2,, n 因而 k k n n = ⋅ ⋅µ = µ 1

特别地, 样本均值灭是总体期望E(X)的无偏估计量 样本二阶原点矩4,=1∑X?是总体二阶 i1 原点矩4,=E(X2)的无偏估计量
特别地, 样本二阶原点矩 ∑= = n i Xi n A 1 2 2 1 是总体二阶 原点矩µ2 = E(X 2 ) 的无偏估计量 样本均值X 是总体期望 E( X ) 的无偏估计量

例2设总体X的期望E(X)与方差D(X)存在, (X1,X2,,Xm)是X的一个样本,n>1 (Is=2(X,-2不是D(X)的无偏估计量: i=l 2s=,龙(x,-x是DX)的无偏估计量 n-1 证前己证2(x,-x2-2x-x i=1 i1 E(X)=E(X)=4,D(X;)=D(X)=o2 E(X=E(X=,DR=
例2 设总体 X 的期望 E( X )与方差 D( X )存在, ( , , , ) X1 X2 Xn 是 X 的一个样本, n > 1 (1) ∑ 不是 D( X ) 的无偏估计量; = = − n i n Xi X n S 1 2 2 ( ) 1 (2) ∑ 是 D( X ) 的无偏估计量. = − − = n i Xi X n S 1 2 2 ( ) 1 1 证 2 1 2 1 2 1 ( ) 1 X X n X X n n i i n i ∑ i − = ∑ − = = 前已证 . 证明 2 E(Xi ) = E(X) = µ , D(Xi ) = D(X) = σ n E X E X D X 2 ( ) ( ) , ( ) σ = = µ =
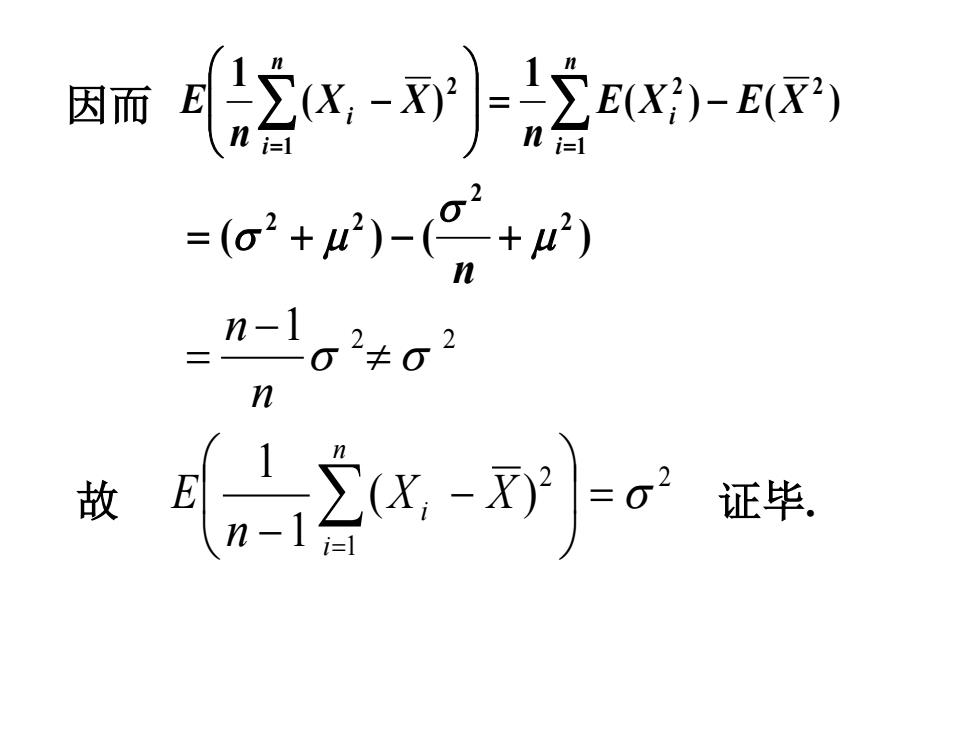
因而2x-W24- =(a2+)-g+2) =n-1g2 故 cn2-wj。 证毕
( ) ( ) 1 ( ) 1 2 1 2 1 2 E X E X n X X n E n i i n i i = − ∑ − ∑ = = 因而 ( ) ( ) 2 2 2 2 µ σ = σ + µ − + n 1 2 2 σ ≠ σ − = n n 2 1 2 ( ) 1 1 = σ − − ∑ = n i Xi X n 故 E 证毕

例3设X1,X2,,Xm)是总体X的一个样本, X~B(n,p)n>1,求p2的无偏估计量. 解由于样本矩是总体矩的无偏估计量以及 数学期望的线性性质,只要将未知参数表示成 总体矩的线性函数,然后用样本矩作为总体矩 的估计量,这样得到的未知参数的估计量即为 无偏估计量. 令X=E(X)=np 1x?=E(X2)=(np)2+p(1-p) m i=l
例3 设( , , , ) X1 X2 X m 是总体 X 的一个样本 , X ~ B ( n , p ) n > 1 , 求 p 2 的无偏估计量. 解 由于样本矩是总体矩的无偏估计量以及 数学期望的线性性质, 只要将未知参数表示成 总体矩的线性函数, 然后用样本矩作为总体矩 的估计量, 这样得到的未知参数的估计量即为 无偏估计量. 令 X = E(X ) = np ( ) ( ) (1 ) 1 2 2 1 2 X E X np np p m m i ∑ i = = + − =
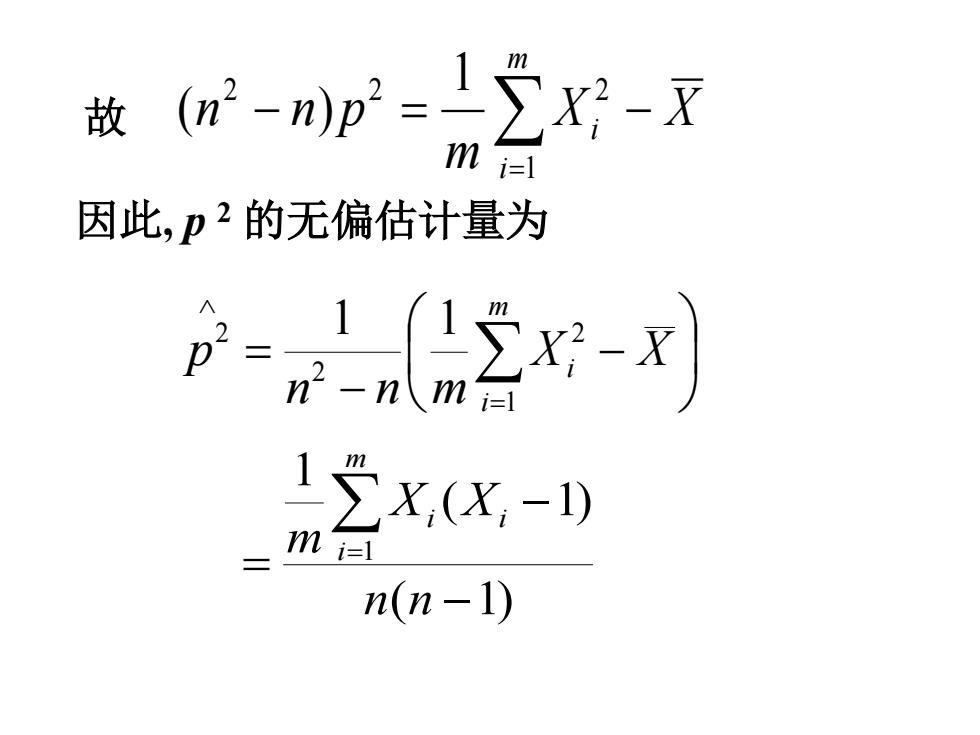
故m2-mp2=12x-X m i=1 因此,p2的无偏估计量为 p-eΣ-了 12X,(X,-1) m i=l n(n-1)
− − = ∑ = ∧ X X n n m p m i i 1 2 2 2 1 1 因此, p 2 的无偏估计量为 ( 1) ( 1) 1 1 − − = ∑ = n n X X m m i i i 故 X X m n n p m i − = ∑ i − =1 2 2 1 2 ( )

例4设总体X的密度函数为 x>0, fxQ-0 0>0为常数 x≤0 (X1,X2,…,Xn)为X的一个样本 证明灭与nmin{X1,X2,,X,n}都是0的无偏 估计量 证 X~E E(X)=0 故E(X)=E(X)=O X是0的无偏估计量
例4 设总体 X 的密度函数为 ≤ > = − 0 0 0, 1 ( ; ) x e x f x x θ θ θ θ > 0 为常数 ( , , , ) X1 X2 Xn 为 X 的一个样本 证明 X 与 min{ , , , } n X1 X2 Xn 都是θ 的无偏 估计量 证 θ θ = ( ) 1 X ~ E E X 故 E(X ) = E(X ) = θ X 是θ 的无偏估计量

令 Z=min{X1,X2,…,Xn} Fz()=1-P(X1>,X2>,,Xn>z) =1-P(X1>z)P(X2>z)…P(Xm>z) e1-i0-X,≤0 0 z<0 z<0 1-e z≥0 fz(z)=了n nz z≥0 即 Z-E E=号 E(nZ)=0 故nZ是0的无偏估计量
min{ , , , } 令 Z = X1 X2 Xn ≥ > n > ∏ = = − − ≤ n i i P X z 1 1 (1 ( )) ( ) 1 ( , , , ) 1 2 F z P X z X z X z Z = − > > n >