
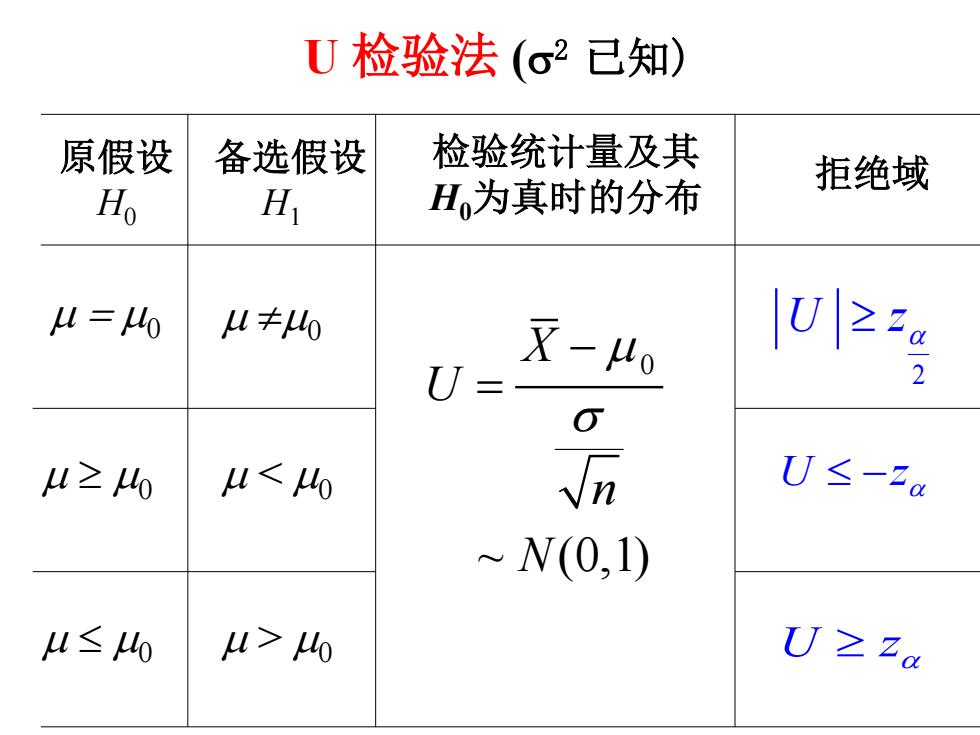
8.2单个正态总体的参数检验 1、关于4的检验 拒绝域的推导 给定显著性水平与样本值(X1,2,,Xn) 设X~W(4,o),σ已知,需检验: H:u=40:H1:u+40 构造统计量 U=X-1o-N(0.) n
8.2 单个正态总体的参数检验 拒绝域的推导 设 X ~N ( µ, σ2),σ2 已知,需检验: H0 : µ = µ0 ; H1 : µ ≠µ0 构造统计量 ~ (0,1) 0 N n X U σ − µ = 给定显著性水平α与样本值(x1,x2,…,xn ) 1、关于µ 的检验

P(拒绝H|H为真) =P(X-4购≥k4=4)=Pa(X-4购≥k) =P( X-Ho )=PH X-Ho ≥Z)= 取k三Zg 所以本检验的拒绝域为 U≥ U检验法
P(拒绝H0|H0为真) ( ) = − µ0 ≥ µ = µ0 P X k ( ) 0 0 P X k = H − µ ≥ ( ) 0 0 n k n X PH σ σ µ ≥ − = α σ µ ≥ α = − = ( ) 2 0 0 Z n X PH n k Z σ α 2 取 = 所以本检验的拒绝域为 0: 2 U ≥ zα U 检验法
U检验法(o2已知) 原假设 备选假设 检验统计量及其 拒绝域 Ho H H为真时的分布 4=0 4丰0 U= X-Ho 10iz% u≥40 440 U≥za
µ = µ0 µ ≠µ0 µ ≥ µ0 µ ≤ µ0 µ µ0 2 U z ≥ α U z ≤ − α U z ≥ α U 检验法 (σ2 已知) 原假设 H0 备选假设 H1 检验统计量及其 H0为真时的分布 拒绝域 0 ~ (0,1) X U n N µ σ − =
T检验法(σ2未知) 原假设 备择假设 检验统计量及其 Ho H H为真时的分布 拒绝域 W=0 4≠0 |Tl≥1a T= X-Ho S W≥40 L40 T≥ta
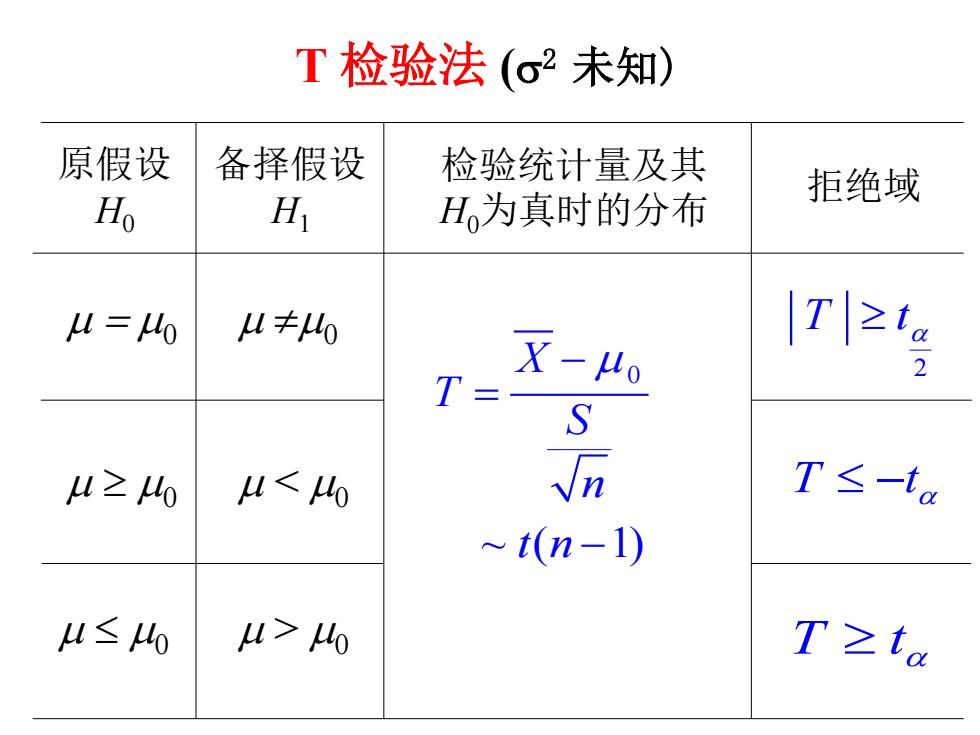
µ = µ0 µ ≠µ0 µ ≥ µ0 µ ≤ µ0 2 T t ≥ α µ µ0 T t ≥ α T t ≤ − α 0 ~ ( 1) X T S n t n − µ = − T 检验法 (σ2 未知) 原假设 H0 备择假设 H1 检验统计量及其 H0为真时的分布 拒绝域

例某厂生产小型马达,其说明书上写着: 这种小型马达在正常负载下平均消耗电流不 会超过0.8安培. 现随机抽取16台马达试验,求得平均消 耗电流为0.92安培,消耗电流的标准差为 0.32安培. 假设马达所消耗的电流服从正态分布, 取显著性水平为=0.05,问根据这个样 本,能否否定厂方的断言?
例 某厂生产小型马达, 其说明书上写着: 这种小型马达在正常负载下平均消耗电流不 会超过0.8 安培. 现随机抽取16台马达试验, 求得平均消 耗电流为0.92安培, 消耗电流的标准差为 0.32安培. 假设马达所消耗的电流服从正态分布, 取显著性水平为α = 0.05, 问根据这个样 本, 能否否定厂方的断言?

解根据题意待检假设可设为 H:4≤0.8; H1:4>0.8 σ未知,故选检验统计量: T X-4 S/V16 ~T15) 查表得t.0s(15)=1.753,故拒绝域为 x-0.8 >1.7 3→x>0.8+1.75303 =0.94 s//n 4 现x=0.92<0.94 故接受原假设,即不能否定厂方断言
H0 : µ ≤ 0.8 ; H1 : µ > 0.8 σ 未知, 故选检验统计量: ~ (15) / 16 X T T S − µ = 查表得 t0.05(15) = 1.753, 故拒绝域为 0.8 1.753 / x s n − > ⇒ 0.32 0.8 1.753 0.94 4 x >+ = 现 x = < 0.92 0.94 故接受原假设, 即不能否定厂方断言. 解 根据题意待检假设可设为
2、关于o2的检验 x检验法 原假设 备择假设 检验统计量及其在 拒绝域 H H H为真时的分布 02=002 02≠002 x2≤g(m) ∑X- 或x2之X(m) 022002 02002 X2≥xa(n)
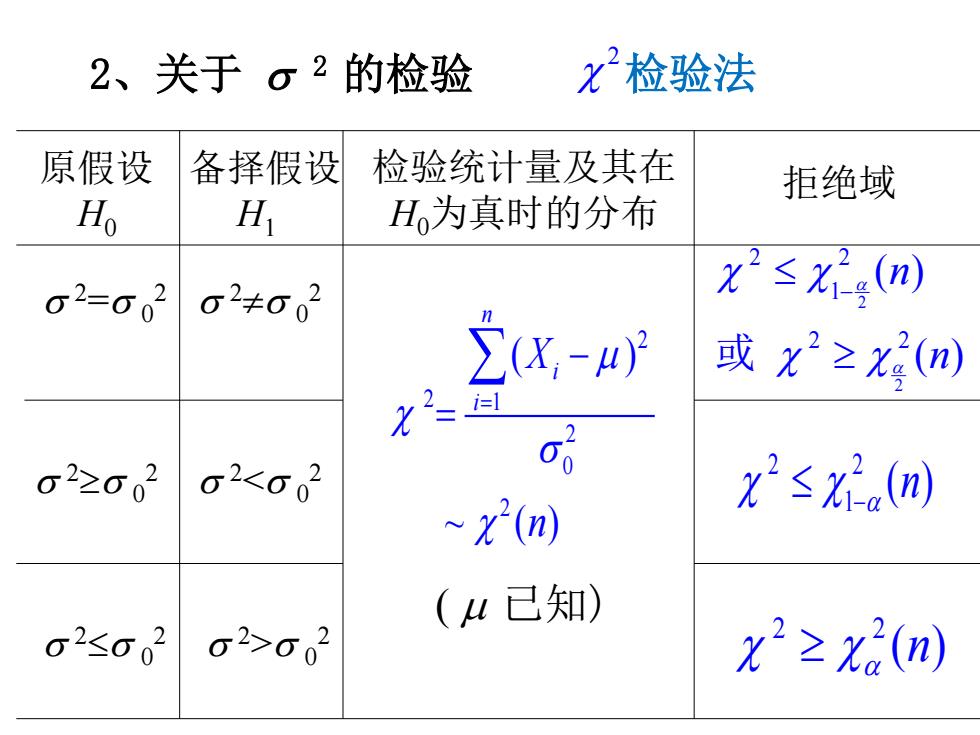
σ 2≤σ 0 2 σ 2>σ 0 2 2 2 ( ) n χ χα ≥ σ 2<σ 0 2 2 2 1 ( ) n α χ χ − σ ≤ 2≥σ 0 2 σ 2=σ 0 2 σ 2≠σ 0 2 原假设 H0 备择假设 H1 检验统计量及其在 H0为真时的分布 拒绝域 检验法 2 χ ( µ 已知) 2 2 1 2 0 2 ( ) ~ () n i i X n µ χ σ χ = − = ∑ 2 2 2 2 1 2 2 ( ) ( ) n n α α χ χ χ χ − ≤ 或 ≥ 2、关于 σ 2 的检验

原假设 备择假设 检验统计量及其在 拒绝域 H H H为真时的分布 02=002 02≠002 x2≤2gn-l1) x2=n-灯2 或x2≥xn-0 σ22002 02002 (4未知) x2≥a2(n-10
σ 2≤σ 0 2 σ 2>σ 0 2 2 2 ( 1) n χ χα ≥ − σ 2<σ 0 2 2 2 1 ( 1) n α χ χ − σ ≤ − 2≥σ 0 2 σ 2=σ 0 2 σ 2≠σ 0 2 2 2 2 2 1 2 2 ( 1) ( 1) n n α α χ χ χ χ − ≤ − 或 ≥ − 原假设 H0 备择假设 H1 检验统计量及其在 H0为真时的分布 拒绝域 2 2 2 0 2 ( 1) ~ ( 1) n S n χ σ χ − = − ( µ 未知)

例假设某品牌某型号的纯电动汽车充满电后行驶的 里程数(单位:公里)服从正态分布,今从中随机地 抽出10辆该型号的车,测得数据如下: 317 287 244 330 301 251 284 279 265 244 检验水平为0=0.05 试问:是否可以认为该厂生产的新能源汽车的续航 里程的方差为400?
例 假设某品牌某型号的纯电动汽车充满电后行驶的 里程数(单位:公里)服从正态分布,今从中随机地 抽出10辆该型号的车,测得数据如下: 317 287 244 330 301 251 284 279 265 244 检验水平为 试问:是否可以认为该厂生产的新能源汽车的续航 里程的方差为400? α = 0.05

解由题意知要检验 H:o2=400,H:o2≠400 因为山未知,故采用如下统计量 x 9S2 400 当H。为真时,x2~x(9)。此时拒绝域为 W={x2≤65(9)U{x2≥2625(9)} 查表得 W={x2≤2.70U{x2≥19.02}
2 2 0 0 H H : 400, : 400 σ σ = ≠ µ 2 2 9 400 S χ = 解 由题意知要检验 因为 未知,故采用如下统计量 , H0 2 2 χ χ ~ (9) { } { } 22 22 0.975 0.025 W =≤ ≥ χχ χχ (9) (9) 当 为真时, 。此时拒绝域为 查表得 { } { } 2 2 W =≤ ≥ χ χ 2.70 19.02