
2.2 离散型随机变量及其概率分布 离散随机变量及分布律 定义若随机变量X的可能取值是有限多个 或无穷可列多个,则称X为离散型随机变量 描述离散型随机变量的概率特性常用它的概 率分布或分布律,即 P(X=xx)=pk,k=1,2,… 或 X X1 X2 XK P2 Pk
2.2 离散型随机变量及其概率分布 离散随机变量及分布律 定义 若随机变量 X 的可能取值是有限多个 或无穷可列多个,则称 X 为离散型随机变量 描述离散型随机变量的概率特性常用它的概 率分布或分布律,即 P(X = xk ) = pk , k =1,2, X x1 x2 … xK … P p1 p2 … pk … 或

或 X~ X 水… 概率分布的性质 P%≥0,k=1,2,… 非负性 ∑P=1 规范性 k=
X ~ 或 1 2 k xx x 1 2 k pp p 概率分布的性质 pk ≥ 0, k =1,2, 非负性 1 1 ∑ = ∞ k= k p 规范性
例设一汽车在开往目的地的途中需经过4盏 信号灯,每盏信号灯独立地以概率p允许 汽车通过。令X表示首次停下时已通过的 信号灯的盏数,求X的概率分布与 p=0.4时的分布函数。 出发地 目的地 解 P(X=k)=p(1-p),k=0,1,2,3 P(X=4)=p4, k=4
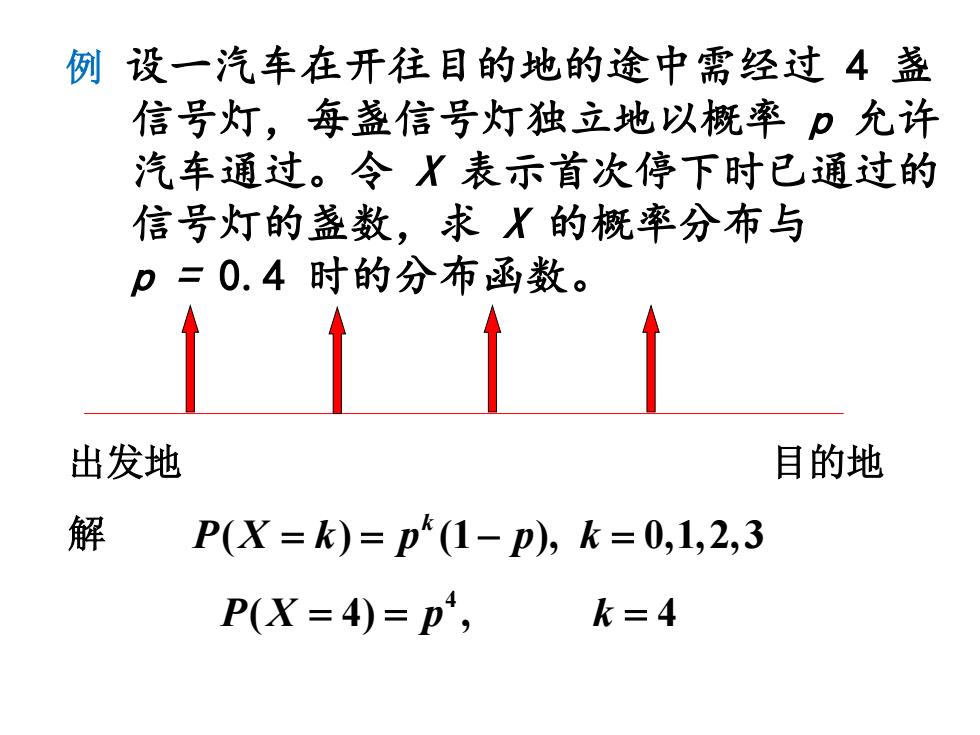
例 设一汽车在开往目的地的途中需经过 4 盏 信号灯,每盏信号灯独立地以概率 p 允许 汽车通过。令 X 表示首次停下时已通过的 信号灯的盏数,求 X 的概率分布与 p = 0.4 时的分布函数。 出发地 目的地 ( ) (1 ), 0,1,2,3 k 解 PX k p p k == − = 4 PX p k ( 4) , 4 = = =

当 p=0.4 k 0 1 2 3 4 0.60.4×0.60.42×0.60.43×0.6 0.44
当 p = 0.4 0.6 0.4´0.6 0.42´0.6 0.43´0.6 0.44 k pk 0 1 2 3 4
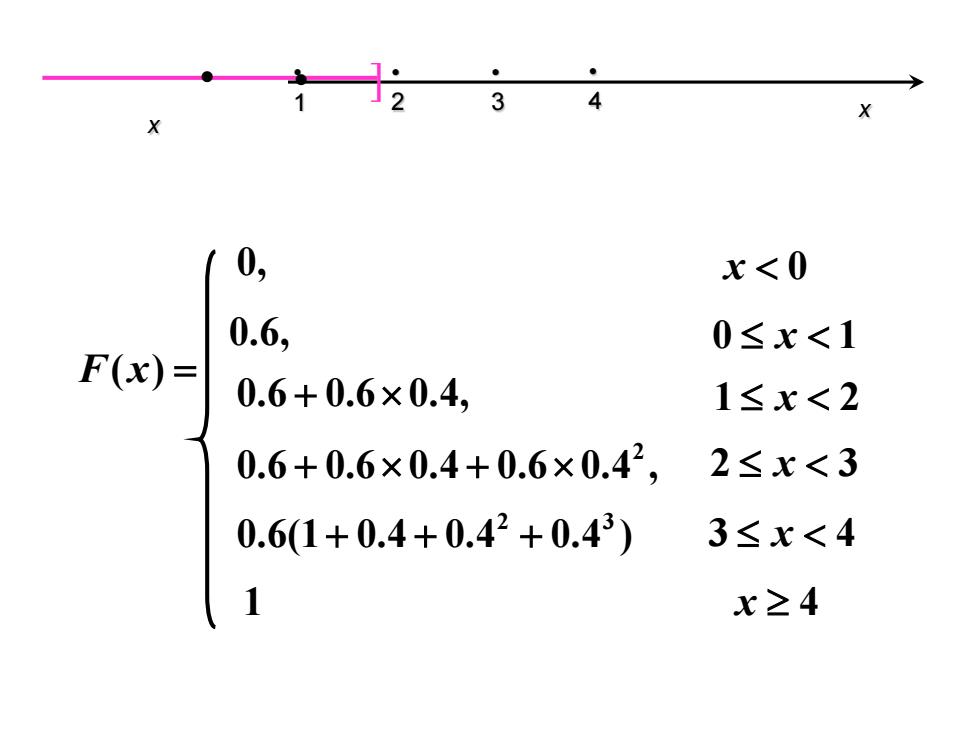
1 3 4 0, x<0 0.6, 0≤x<1 F(x)= 0.6+0.6×0.4, 1≤x<2 0.6+0.6×0.4+0.6×0.42, 2≤x<3 0.6(1+0.4+0.42+0.43) 3≤x<4 1 x≥4
• 0 • 1 • 2 • 3 • 4 x x ] ] 0.6 0.6 0.4, + × 1 2 ≤ < x 0.6, 0 1 ≤ < x 0, x < 0 2 0.6 0.6 0.4 0.6 0.4 , +×+× 2 3 ≤ < x 2 3 0.6(1 0.4 0.4 0.4 ) ++ + 3 4 ≤ < x 1 x ≥ 4 F x( ) = ]• • • ]
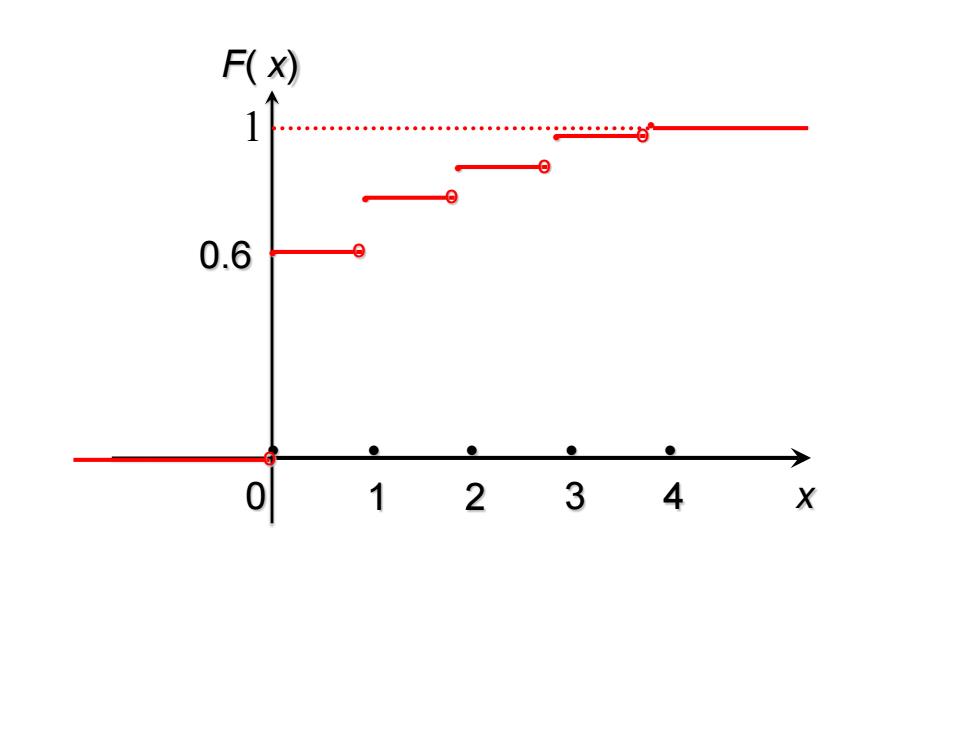
F(x) g年88。。。。0e年。00.0.8。。。。。。80年88s。99年中白 0.6 4 X
• 0 • 1 • 2 • 3 • 4 x F( x) o • o 1 • o • o • o• 0.6

离散随机变量及分布函数 F(x)=P(X<x)=P((X=x)) Xk≤X =∑P(X=x)=∑P Xk≤X Xk≤x Pk=P(X=X)=F(xk)-F(K) 其中k-1<Xk· F()是分段阶梯函数,在X的可能取值 X处发生间断。间断点为第一类跳跃间断点,在 间断点处有跃度Pk
离散随机变量及分布函数 ( ) ( ) (( )) x x k k F x P X x P X x ≤ = ≤ = = ∑ ∑ ≤ ≤ = = = x x k x x k k k P(X x ) p 其中 . k k x < x −1 F( x) 是分段阶梯函数, 在 X 的可能取值 xk 处发生间断. 间断点为第一类跳跃间断点,在 间断点处有跃度 pk ( ) ( ) ( ) k = = k = k − k−1 p P X x F x F x

例: 设随机变量的分布律为 -1 2 3 Pk 4 4 求X的分布函数,并求PX≤)PsX≤P2sX≤) 解:X的分布函数为 0 x<-1 0 x<-1 1 即 1 -1≤x<2 -1≤x<2 4 F(x)= F(x)= 4 1.1 3 2≤x<3 2≤x<3 42 4 1 3≤x 3≤x
例: 设随机变量的分布律为 求X 的分布函数,并求 ), 2 1 P(X ≤ ), (2 3) 2 5 2 3 P( < X ≤ P ≤ X ≤ k p -1 2 3 4 1 4 1 2 1 解: X的分布函数为 即 F(x) = 0 1 1 1 2 4 1 1 2 3 4 2 1 3 x x x x < − −≤ < + ≤< ≤ F(x) = 0 1 1 1 2 4 3 2 3 4 1 3 x x x x < − −≤ < ≤ < ≤ X

注:对离散型随机变量用概率分布(或分布律) 比用分布函数计算这些概率更方便,所以描述 离散性随机变量通常用概率分布(或分布律) 例对一目标进行射击,且各次射击相互独立, 若每次击中目标的概率为p(0〈p〈1), 次一次地射击直到击中目标为止。求所需射击 次数X的概率分布。 P(X=k)=p(1-p)-1 k=1,2,… 注:此分布称为几何分布
注:对离散型随机变量用概率分布(或分布律) 比用分布函数计算这些概率更方便,所以描述 离散性随机变量通常用概率分布(或分布律) 例 对一目标进行射击,且各次射击相互独立, 若每次击中目标的概率为p (0 < p < 1), 一 次一次地射击直到击中目标为止。求所需射击 次数 X 的概率分布。 P ( X = k ) 1 (1 )k p p − = − k = 1, 2, 注:此分布称为几何分布

例一门大炮对目标进行轰击,假定此目标必须 被击中?次才能被摧毁。若每次击中目标的 概率为p(0<p〈),且各次轰击相互独立, 一次一次地轰击直到摧毁目标为止。求所需 轰击次数X的概率分布。 解P(X=k)=P(前k-1次击中r-1次, 第k次击中目标) =Cp(1-p)-·p =Cp'(1-p)- k=r,P+1,… 注:此分布称为帕斯卡分布
例 一门大炮对目标进行轰击,假定此目标必须 被击中r 次才能被摧毁。若每次击中目标的 概率为p (0 < p < 1),且各次轰击相互独立, 一次一次地轰击直到摧毁目标为止。求所需 轰击次数 X 的概率分布。 解 P ( X = k ) 1 1 1 (1 ) r r k r Cp p p k −− − = −⋅ − 1 1 (1 ) r r kr Cp p k − − = − − k rr = + , 1, 注:此分布称为帕斯卡分布 = P ( 前 k –1次击中 r – 1次, 第 k 次击中目标)