
第一章随机事件和概 率
第一章 随机事件和概 率 1

1.1随机事件及其运算 。 案例1调查上海市金融行业对从业人员的工作满意 度,如果把满意度分为“满意”、“基本满意” “不满意”、特别不满意”四种,随机抽查一个 从业人员,我们考查他的满意度。由于是随机抽取, 因此所得到的答案具有一定的随机性。 ·案例2考查某城市每周交通事故数,由于每周交通 事故数不一定相同,具有一定的随机性。 ·案例3考查某地铁旁边的早餐店每天早餐中豆浆的 需求量(单位:袋),每天的需求量都不一定相同, 也具有一定的随机性。 案例4扔飞镖或者射击打靶,每次击中的点,也具 有一定的随机性。 2
1.1 随机事件及其运算 • 案例1 调查上海市金融行业对从业人员的工作满意 度,如果把满意度分为“满意”、“基本满意”、 “不满意”、“特别不满意”四种,随机抽查一个 从业人员,我们考查他的满意度。由于是随机抽取, 因此所得到的答案具有一定的随机性。 • 案例2 考查某城市每周交通事故数,由于每周交通 事故数不一定相同,具有一定的随机性。 • 案例3 考查某地铁旁边的早餐店每天早餐中豆浆的 需求量(单位:袋),每天的需求量都不一定相同, 也具有一定的随机性。 • 案例4 扔飞镖或者射击打靶,每次击中的点,也具 有一定的随机性。 2

随机试验 >可在相同条件下重复进行; >所有可能结果不止一个,而且在试验之前 应该是已知的; >每次试验后所得到的结果应该在已知所有 可能结果中,并且事先无法预知会出现哪 个结果
随机试验 可在相同条件下重复进行; 所有可能结果不止一个,而且在试验之前 应该是已知的; 每次试验后所得到的结果应该在已知所有 可能结果中,并且事先无法预知会出现哪 个结果。 3
本课程的主要研究问题之一: 随机试验中某些可能发生,也可能不发生的事件 (称为随机事件)发生的可能性大小(概率) 样本空间与随机事件
本课程的主要研究问题之一: 随机试验中某些可能发生,也可能不发生的事件 (称为随机事件)发生的可能性大小(概率) 样本空间与随机事件 4

样本空间一随机试验E所有可能的结果 组成的集合称为样本空间记为2 样本空间的元素,即E的直接结果,称为 样本点(or基本事件)常记为w,2={w} 随机事件一2的子集,记为A,B, 它是满足某些条件的样本点所组成的集合 注:随机事件是样本空间的一个子集,它是满 足某些条件的样本点所组成的集合
样本空间—— 随机试验E 所有可能的结果 样本空间的元素, 即E 的直接结果, 称为 随机事件 —— W的子集, 记为 A ,B ,… 它是满足某些条件的样本点所组成的集合. 组成的集合称为样本空间 记为W 样本点(or基本事件) 常记为w ,W = {w} 注: 随机事件 是样本空间的一个子集,它是满 足某些条件的样本点所组成的集合。 5

案例1调查上海市金融行业对从业人员的工作满意度,如果把 满意度分为“满意”、“基本满意”、“不满意”、“特别不 满意”四种,随机抽查一个从业人员,我们考查他的满意度。 2=“满意”、“基本满意”、“不满意”、“特别不满意”} 比如我们关心的是第个从业人员的答案是不是 A=“满意”或者“基本满意”, 案例2考查某城市每周交通事故数 2=0,1,2,3,} B=“下周的交通事故数不超过2起” 案例3考查某地铁旁边的早餐店每天早餐中豆浆的需求量(单位:袋) 2={0,1,2,3,…} C=“明天早上的豆浆销量超过100袋” 6
案例1 调查上海市金融行业对从业人员的工作满意度,如果把 满意度分为“满意”、“基本满意”、“不满意”、“特别不 满意”四种,随机抽查一个从业人员,我们考查他的满意度。 Ω = { } “满意” 、 “基本满意” 、 “不满意” 、 “特别不满意” 案例2 考查某城市每周交通事故数 Ω = { } 0,1,2,3, 案例3考查某地铁旁边的早餐店每天早餐中豆浆的需求量(单位:袋) Ω = { } 0,1,2,3, 比如我们关心的是第i个从业人员的答案是不是 A = “满意”或者“基本满意”; B = “下周的交通事故数不超过2起” C = “明天早上的豆浆销量超过100袋” 6

基本事件一仅由一个样本点组成的子集 它是随机试验的直接结果每次试验必定发 生且只可能发生一个基本事件 随机事件发生一 组成随机事件的一个样 本点发生 必然事件—全体样本点组成的事件,记为 2,每次试验必定发生的事件 不可能事件一不包含任何样本点的事件, 记为Φ,每次试验不发生的事件
基本事件 —— 仅由一个样本点组成的子集 它是随机试验的直接结果,每次试验必定发 生且只可能发生一个基本事件. 必然事件——全体样本点组成的事件,记为 W, 每次试验必定发生的事件. 随机事件发生 —— 组成随机事件的一个样 本点发生 不可能事件——不包含任何样本点的事件, 记为F ,每次试验不发生的事件. 7
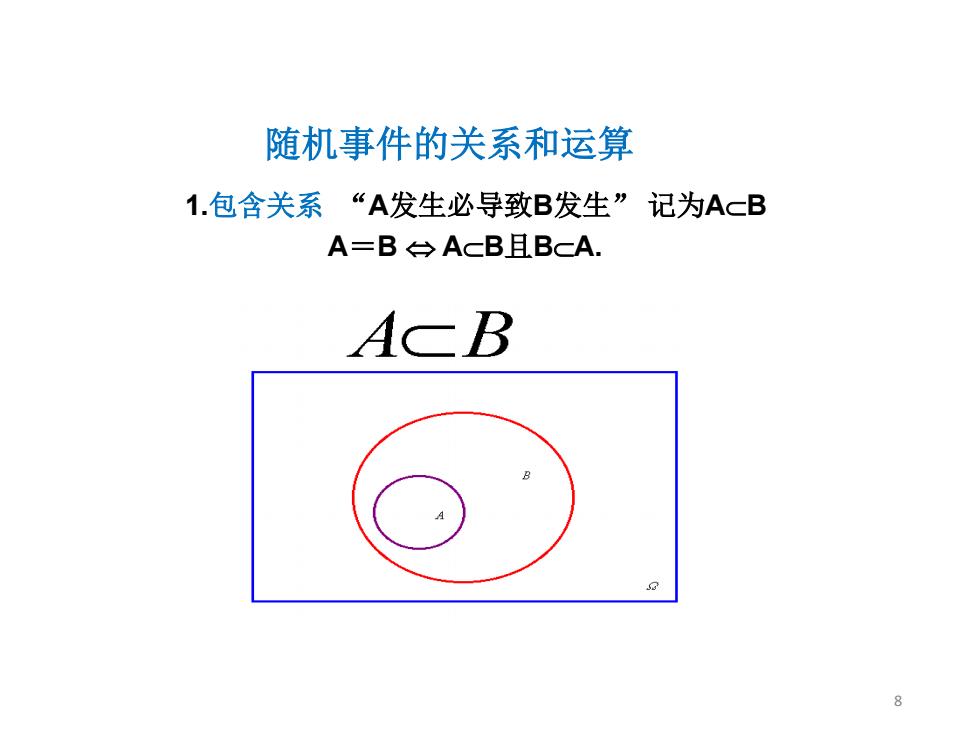
随机事件的关系和运算 1.包含关系“A发生必导致B发生”记为AB A=B÷AcB且BcA. 8
1.包含关系 “A发生必导致B发生” 记为A⊂B A=B ⇔ A⊂B且B⊂A. 随机事件的关系和运算 8

2.和事件:“事件A与B至少有一个发生”,记作AUB AOB n个事件ApA2,An至少有一个发生,记作UA 可列个事件A,A2,Av…至少有一个发生,记作UA i-1 9
2.和事件: “事件A与B至少有一个发生”,记作A∪B n个事件A1, A2,…, An至少有一个发生,记作 1 n i i A= 可列个事件A1, A2,…, An,…至少有一个发生,记作 1 i i A ∞ = 9
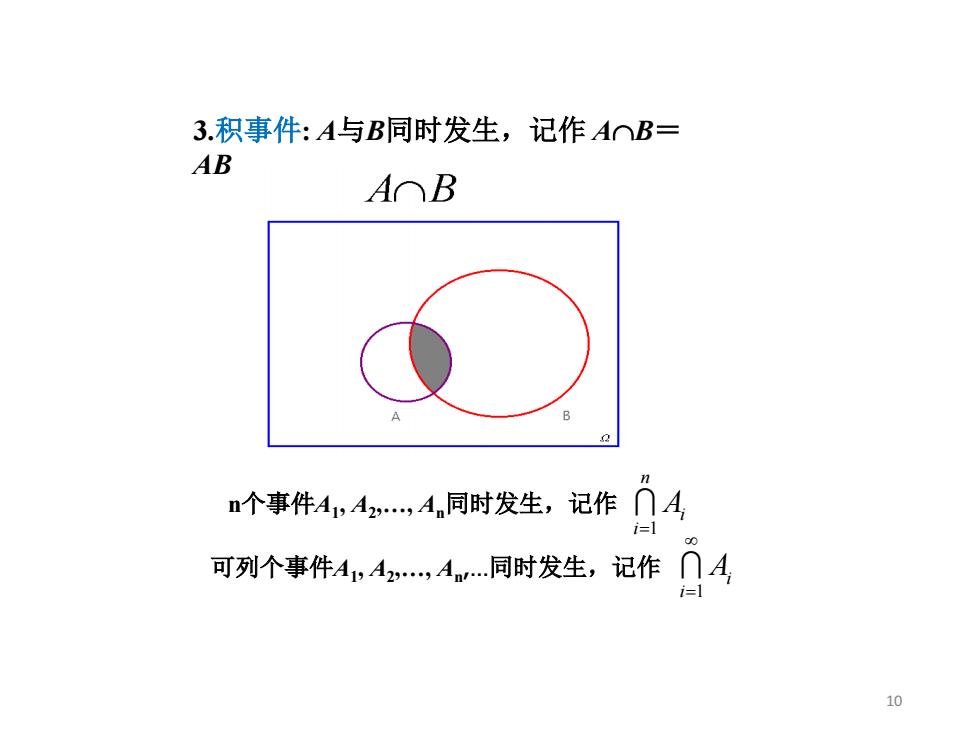
3.积事件:A与B同时发生,记作A∩B= AB A⌒B n个事件4,A,,An同时发生,记作∩A i=1 可列个事件A,A2,A…同时发生,记作∩A 10
3.积事件: A与B同时发生,记作 A∩B= AB n个事件A1, A2,…, An同时发生,记作 1 n i i A= 可列个事件A1, A2,…, An,…同时发生,记作 1 i i A ∞ = 10