华东理工大学：《线性代数》课程电子教案（PPT课件）第一章 矩阵

《线性代数》知识篇五个知识点内在联系图： 矩阵 怼 人的色 行列式 线性方程组)一一对应 (向量组 《特征问题与二次型 上页 回

《线性代数》知识篇五个知识点内在联系图: 矩 阵 线性方程组 行列式 向量组 一 一 对 应 一 一 对 应 一 一 对 应 特征问题与二次型

第一季媒降 第一节矩阵 一、 矩阵概念的引入 二、 矩阵的定义 三、小节、思考题

第一节 矩阵 一、 矩阵概念的引入 二、 矩阵的定义 三、 小节、思考题 第一章 矩阵

一、矩阵概念的引入 0mX1+a2x2+…+0mn=b 1.线性方程组 2x1+2x2+…+02nxn=b2 amxtan2x2++amx=b 系数 的解取决于 a(,j=1,2,,n 常数项b,(i=1,2,,n) 上页

       + + + = + + + = + + + = n n nn n n n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1 1. 线性方程组 的解取决于 a (i, j 1,2, ,n), 系数 ij =  b (i , , ,n) 常数项 i = 1 2  一、矩阵概念的引入

线性方程组的系数与常数项按原位置可排为 12 b b, 对线性方程组的 。。 研究可转化为对 这张表的研究. nn 上页 回

              n n nn n n n a a a b a a a b a a a b         1 2 21 22 2 2 11 12 1 1 对线性方程组的 研究可转化为对 这张表的研究. 线性方程组的系数与常数项按原位置可排为

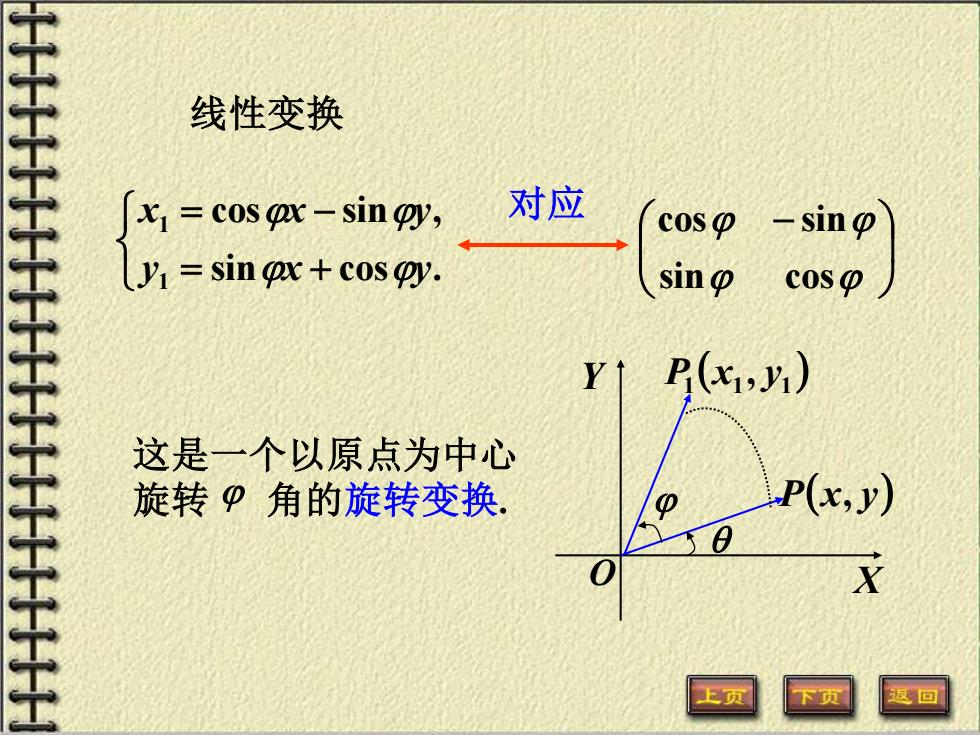
线性变换 x=cos x-sin oy, 对应 cos p -sin y=sin ox+cos oy. sin coso 这是一个以原点为中心 旋转P角的旋转变换。 上页

线性变换    = + = − sin cos . cos sin , 1 1 y x y x x y     对应       −     sin cos cos sin X Y O   P(x, y) ( ) 1 1 1 P x , y 这是一个以原点为中心 旋转  角的旋转变换

二、矩阵的定义 由mxn个数a,(i=1,2,,m;j=1,2,,n) 排成的m行n列的元数表 11 L12 21 L22 … @2n 称为mXn维矩阵.简称m×n矩阵.记作 上页 回

二、矩阵的定义 由 个数 排成的 行 列的元数表 m n m n a (i m j n) ij = 1,2,  , ; = 1,2,  , m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 称为 mn 维矩阵.简称 m  n 矩阵.记作

L12 A= da 22 2m 矩阵A的 (m,n元 简记为 A=Amon =(ag)=(ag) 这m×n个数称为4的元素，简称为元(a为代表元) 元素是实数的矩阵称为实矩阵 元素是复数的矩阵称为复矩阵 上页

              = m m mn n n a a a a a a a a a A        1 1 21 22 2 11 12 1 简记为 ( ) ( ). ij m n A= Am n = aij = a   ( )元 矩阵 的 m n A , 这 个数称为 的元素,简称为元( 为代表元）. m n A ai j 元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵

例如a=i-j,i,j=1,2,3.则 ）-1 A= 1 0 1 上页 这回

例 如ai j = i − j, i, j = 1,2,3.则           − − − = 2 1 0 1 0 1 0 1 2 A

例如 1 0 3 5 -9 64 是一个2×4实矩阵， 13 6 2i 2 2 2 是一个3×3复矩阵， 24 2 2 2 是个3×1矩阵， (2359) 是一个1×4矩阵， (4)是一个1×1矩阵

例如       − 9 6 4 3 1 0 3 5 是一个 24 实矩阵,           2 2 2 2 2 2 13 6 2i 是一个 33 复矩阵,           4 2 1 是一个 31 矩阵, (2 3 5 9) 是一个 14 矩阵, (4) 是一个 11 矩阵

几种特殊矩阵 (1)行数和列数都等于n的矩阵A,称为n阶 方阵.也可记作A 副（反）对角线 13 例如 是一个3阶方阵. 主对角线 (2)只有一行元素的矩阵 A=(a1,2,…,an) 称为行矩阵（或行向量） 上页 区回

例如           2 2 2 2 2 2 13 6 2i 是一个3 阶方阵. 几种特殊矩阵 (2)只有一行元素的矩阵 ( , , , ), A = a1 a2  an 称为行矩阵(或行向量). . 方阵.也可记作 An (1)行数和列数都等于n的矩阵A, 称为n阶 主对角线 副(反)对角线