
4.3协方差及相关系数 问题对于二维随机变量(X,Y): 己知联合分布 边缘分布 这说明对于二维随机变量,除了每个 随机变量各自的概率特性以外,相互之间 可能还有某种联系.问题是用一个什么样 的数去反映这种联系. 数E(X-EX)Y-EY)) 反映了随机变量X,Y之间的某种关系
4.3 协方差及相关系数 问题 对于二维随机变量(X ,Y ): 已知联合分布 边缘分布 这说明对于二维随机变量,除了每个 随机变量各自的概率特性以外,相互之间 可能还有某种联系. 问题是用一个什么样 的数去反映这种联系. 数 反映了随机变量X ,Y 之间的某种关系 E X EX Y EY (( )( ) − − )

1.协方差 定义称E((X-EX)Y-EY) 为X,Y的协方差.记为 cov(X,Y)=E((X-EX)(Y-EY)) > 若(X,Y)为离散型, cov(X,Y)=∑∑(,-EX)Oy,-EY)pg 义 i=1j1 计 >若(X,Y)为连续型, cov(X,I)=∫∫(x-EX)0y-Efx,y)d
1. 协方差 定义 称 E X EX Y EY (( )( ) − − ) 为X ,Y 的协方差. 记为 cov( , ) ( )( ) X Y E X EX Y EY =− − ( ) 用定义计算 若 ( X ,Y ) 为离散型, 1 1 cov( , ) ( )( ) i j ij i j X Y x EX y EY p ∞ ∞ = = = −− ∑∑ 若 ( X ,Y ) 为连续型, cov( , ) ( )( ) ( , ) X Y x EX y EY f x y dxdy +∞ +∞ −∞ −∞ = −− ∫ ∫

2.相关系数 定义若D(X)>0,D(Y)>0,称 E X-EX)(Y-EY) cov(X,Y) D(X)D(Y) DX)NDO 为X,Y的相关系数,记为 cov(X,Y) Pxy =√DX)ND(Y) 事实上, Pxy =cov(X',Y') Pxy =0, 称X,Y不相关. lPxr|=1, 称X,Y完全相关 0<Pxx<1,称X,Y部分线性相关
2. 相关系数 定义 若D (X ) > 0, D (Y ) > 0 ,称 ( )( ) cov( , ) ( ) () ( ) () X EX Y EY X Y E D X DY D X DY − − = 为X ,Y 的相关系数,记为 cov( , ) ( ) () XY X Y D X DY ρ = 事实上, cov( , ) ∗ ∗ ρ XY = X Y 0, ρ XY = 称 X ,Y 不相关. 1, ρ XY = 称 X ,Y 完全相关. 0 1, < < ρ XY 称 X ,Y 部分线性相关

3.协方差和相关系数的性质 协方差的性质 (1)cov(Y,Y)=cov(Y,X)=E(XY)-E(X)E(Y) (计算公式) (2)cov(ax,bY)=abcov(X,Y) (3)cov(X+Y,Z)=cov(X,Z)+cov(Y,Z) (4)cov(X,X)=D(X) (S)D(X±Y)=D+DY±2cov(X,Y) cov(X,Y)=±(D(X±Y)-DX-DY) (计算会式)
3. 协方差和相关系数的性质 协方差的性质 (2) cov( , ) cov( , ) aX bY ab X Y = (1) cov( , ) cov( , ) ( ) ( ) ( ) X Y Y X E XY E X E Y = = − (3) cov( , ) cov( , ) cov( , ) X YZ XZ YZ += + (4) cov( , ) ( ) X X DX = (5) ( ) D X Y DX DY X Y ±= + ± 2cov( , ) ( ) 1 cov( , ) ( ) 2 X Y D X Y DX DY =± ± − − (计算公式) (计算公式)

(6)cov(X,Y)D(X)D(Y) 当DX)>0,D(Y)>0时,当且仅当 P(Y-E(Y)=t(X-E(X))=1 时,等式成立一Cauchy-Schwarz:不等式 相关系数的性质 (1)川Pxw1 (2)川py=1◆→ Cauchy-Schwarz.不等式 的等号成立 即Y与X有线性关系的概率等于1, 这种线性关系为 Y-E(Y)_+X-E(X) =1 VDY)√D(X)
2 (6) | cov( , ) | ( ) ( ) XY D X DY ≤ 当D(X ) > 0, D(Y ) > 0 时,当且仅当 0 PY EY t X E X ( ( ) ( ( ))) 1 − =− = 时,等式成立 —Cauchy-Schwarz Schwarz不等式 相关系数的性质 (1) | | 1 ρ XY ≤ (2) | | 1 ρ XY = Cauchy-Schwarz不等式 的等号成立 即Y 与X 有线性关系的概率等于1, 这种线性关系为 () ( ) 1 () ( ) Y EY X E X P DY D X − − = ± =
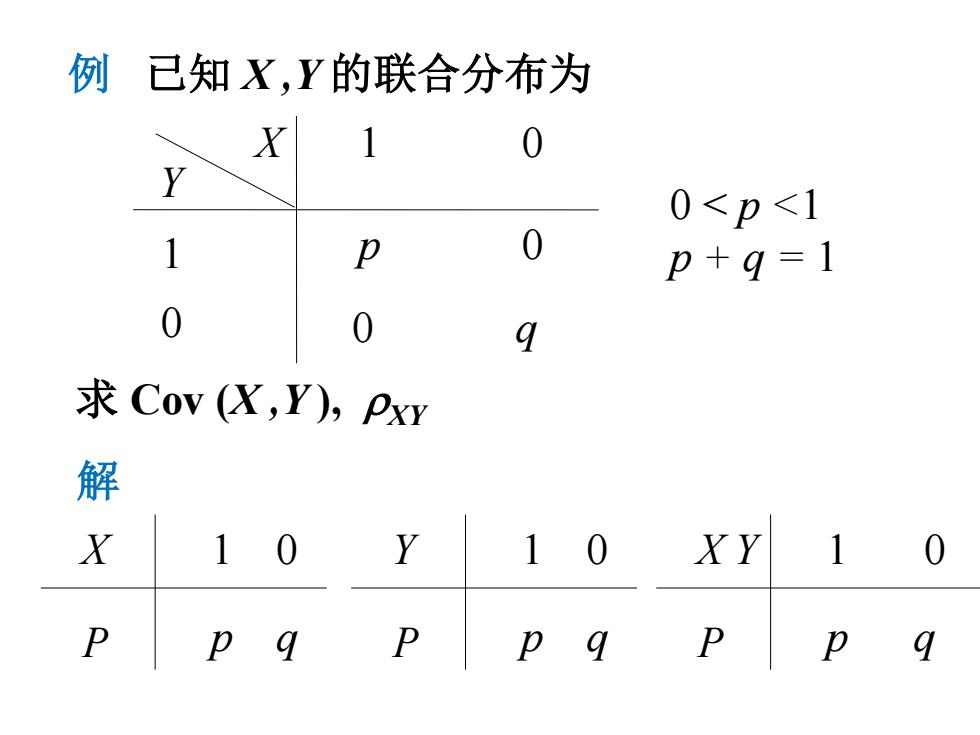
例已知X,Y的联合分布为 X 1 0 0<p<1 1 p 0 p+9=1 0 0 q 求Cov(X,Y),Pxw 解 X 10 1 0 P p②
求 Cov (X ,Y ), ρXY 1 0 p q X P 1 0 p q Y P 例 已知 X ,Y 的联合分布为 X Y 1 0 1 0 p 0 0 q 0 < p <1 p + q = 1 解 1 0 p q X Y P
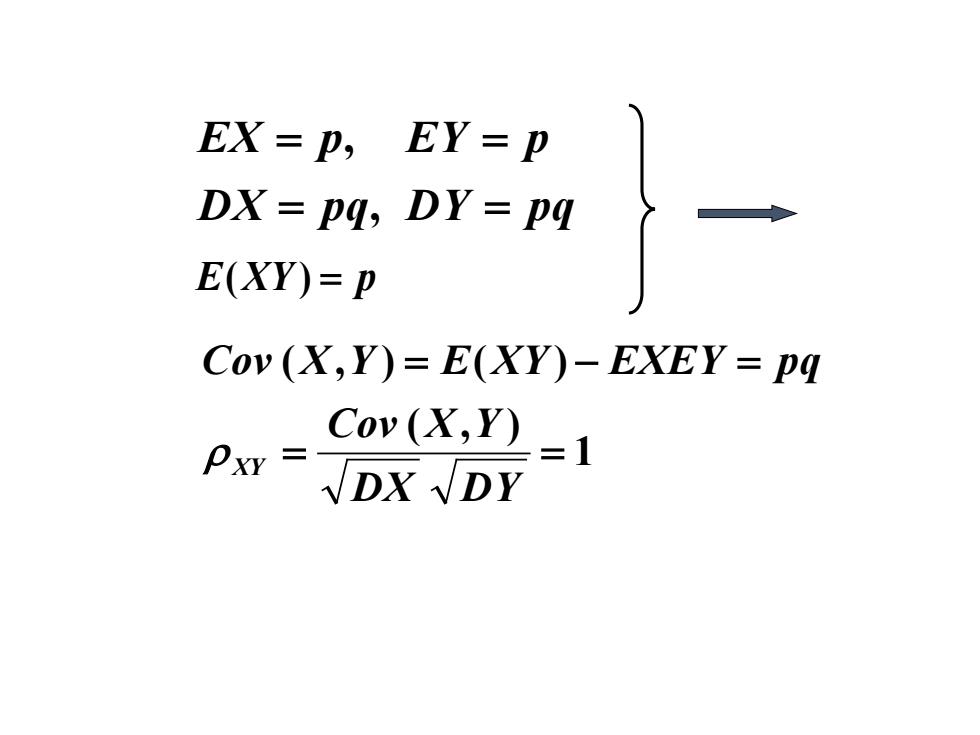
EX=p,EY=P DX=pq,DY=pq E(XY)=P Cov(X,Y)=E(XY)-EXEY=pq =1 Cov(X,Y) PxY-DX DY
DX pq DY pq EX p EY p = = = = , , E(XY ) = p 1 ( , ) ( , ) ( ) = = = − = DX DY Cov X Y Cov X Y E XY EXEY pq ρ XY
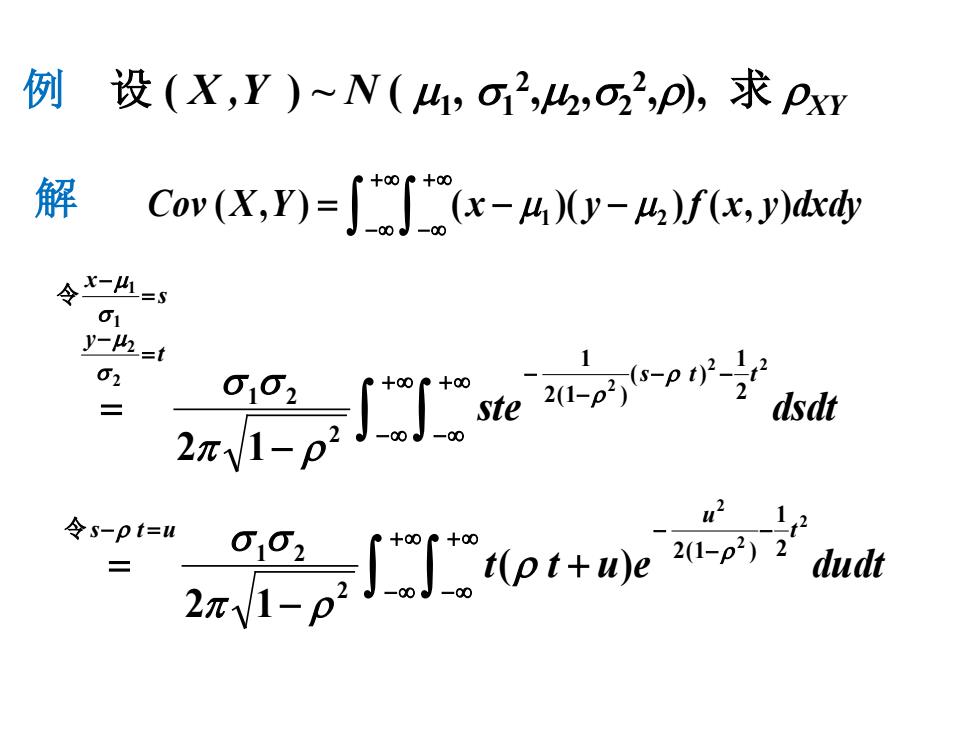
例设(X,Y)~N(h,O2,h2,O2p列,求pxy 解 Cov(X.Y)(x-mXy-)f(x,db 令-4=5 01 y-W=t 2 令s-pt= 2
例 设 ( X ,Y ) ~ N ( µ1, σ1 2 ,µ2,σ2 2 ,ρ), 求 ρXY 解 Cov (X,Y ) (x )( y )f (x, y)dxdy ∫ ∫ 1 2 +∞ −∞ +∞ −∞ = − µ − µ ste dsdt s t t t y s x 2 2 2 2 2 1 1 2 1 ( ) 2(1 ) 1 2 1 2 2 1 − − − ∞ − + −∞ +∞ −∞ = − = − ∫ ∫ − = ρ ρ σ µ σ µ π ρ σ σ 令 t t u e dudt t u s t u 2 2 2 2 1 2(1 ) 2 1 2 ( ) 2 1 − − ∞ − + −∞ +∞ −∞ − = + − = ∫ ∫ ρ ρ ρ π ρ σ σ 令

0102p 12 1 =0102P Px灯=P 若(X,Y)~N(4,σ2,h,22,P) 则X,Y相互独立→X,Y不相关 命题 (X,Y)~N(4,o4,o;p)相互独立 D=0
e du t e dt t u 2 2 2 2 1 2(1 ) 2 2 1 2 2 1 +∞ − −∞ +∞ −∞ − − ∫ ∫ − = ρ π ρ σ σ ρ = σ 1 σ 2ρ ρ ρ XY = 若 ( X ,Y ) ~ N ( µ1, σ1 2 , µ2, σ2 2 , ρ ) 则X ,Y 相互独立 X ,Y 不相关 ρ = 0 ( , ) ~ ( , ; , ; ) 2 2 2 2 命题 X Y N µ1 σ 1 µ σ ρ 相互独立

注:对一般的分布 X,Y相互独立之X,Y不相关 若(X,Y)~N(4,O2,2,O22,p, 则X,Y相互独立→X,Y不相关
若 (X ,Y ) ~ N (µ1, σ1 2 ,µ2,σ2 2 ,ρ), 则X ,Y 相互独立 X ,Y 不相关 注:对一般的分布 X ,Y 相互独立 X ,Y 不相关