
3.2二维随机变量的条件概率 在第一章中,我们介绍了条件概率的概念 在事件B发生的条件下事件A发生的条件概率 P(AB) P(A B)= P(B) 推广到随机变量 设有两个ryX,Y,在给定取某个或某些值 的条件下,求X的概率分布. 这个分布就是条件分布!
在第一章中,我们介绍了条件概率的概念. ( ) ( ) ( | ) P B P AB P A B = 在事件B 发生的条件下事件A 发生的条件概率 推广到随机变量 设有两个r.v X,Y , 在给定Y取某个或某些值 的条件下,求X的概率分布. 这个分布就是条件分布. 3.2 二维随机变量的条件概率

离散型随机变量的条件分布 实际上类似定义在X=x,条件下 率概念在另 种形式随机变量Y的条件分布律, 定义 设(X,Y)是二维离散型随机变量,对 于固定的j,若PY=y}>0,则称 P(X=x= PX=xY=}_,=12, P=} P.j 为在Y=y条件下随机变量X的条件分布律. 作为条件的那个:y,认为取值是给定的, 在此条件下求另一rv的概率分布
实际上是第一章讲过的条件概率概念在另 一种形式下的重复. 定义 设 ( X,Y ) 是二维离散型随机变量,对 于固定的 j,若 P{Y = yj} > 0,则称 为在 Y = yj 条件下随机变量X的条件分布律. P{X= xi |Y= yj }= j i j p p • = ,i=1,2, … 类似定义在 X= xi 条件下 随机变量Y 的条件分布律. { } { } ,i j j PX xY y PY y = = = 作为条件的那个r.v,认为取值是给定的, 在此条件下求另一r.v的概率分布. 一、离散型随机变量的条件分布

条件分布是一种概率分布,它具有概率 分布的一切性质.正如条件概率是一种概率, 具有概率的一切性质, 例如: P{x=xly=y}2012, 2P{X=Y=}=1
条件分布是一种概率分布,它具有概率 分布的一切性质. 正如条件概率是一种概率, 具有概率的一切性质. 例如: PX x Y y { = = ≥ i j} 0 i=1,2, … { } 1 1 i j i PX x Y y ∞ = ∑ = = =
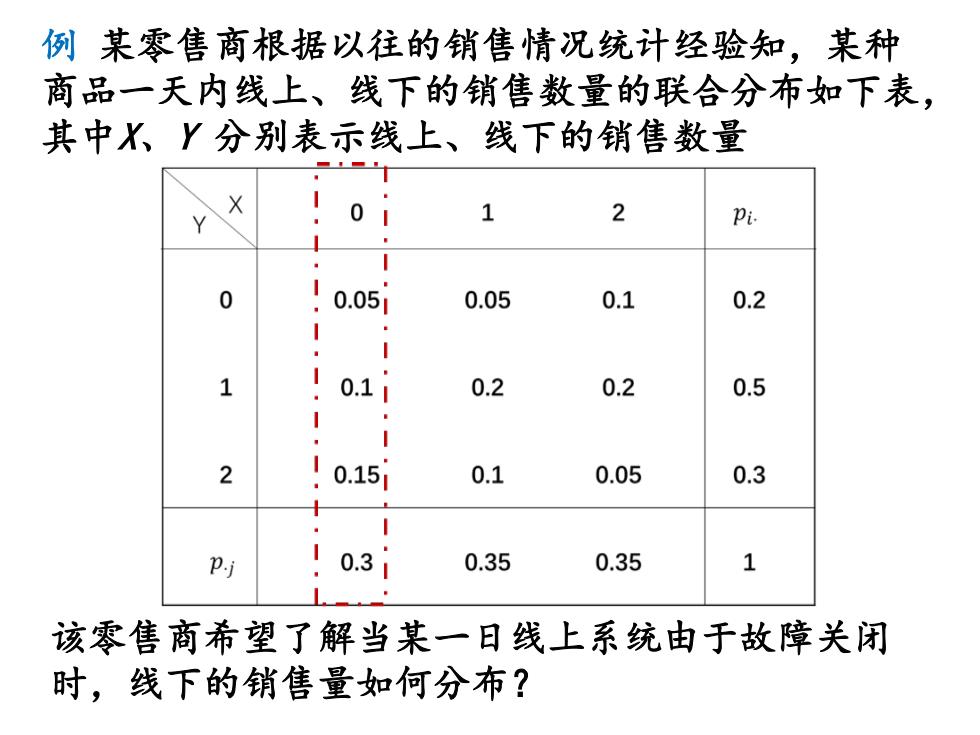
例某零售商根据以往的销售情况统计经验知,某种 商品一天内线上、线下的销售数量的联合分布如下表, 其中X、Y分别表示线上、线下的销售数量 01 2 10.051 0.05 0.1 0.2 0.11 0.2 0.2 0.5 10.151 0.1 0.05 0.3 P.i 0.31 0.35 0.35 该零售商希望了解当某一日线上系统由于故障关闭 时,线下的销售量如何分布?
例 某零售商根据以往的销售情况统计经验知,某种 商品一天内线上、线下的销售数量的联合分布如下表, 其中X、Y 分别表示线上、线下的销售数量 该零售商希望了解当某一日线上系统由于故障关闭 时,线下的销售量如何分布?

分析与解:不难理解当线上系统关闭时,那就相当 于X=0发生了。问题变为求X=0时,随机变量Y的条件 分布。由上述定义中给出条件分布的计算 P(Y=0X=0)= 0.051 0.36 P(Y=1X=0)= 0.11 0.33 P(Y=2X=0)= 0.151 0.3-2 我们可以用表格表示如下: Y=jX=0 0 1 2 P(Y=jX=0) 3
分析与解:不难理解当线上系统关闭时,那就相当 于X=0发生了。问题变为求X=0时,随机变量Y的条件 分布。由上述定义中给出条件分布的计算 0.05 1 ( 0 0) 0.3 6 PY X = = = = 0.1 1 ( 1 0) 0.3 3 PY X = = = = 0.15 1 ( 2 0) 0.3 2 PY X = = = = 我们可以用表格表示如下: Y jX = = 0 0 1 2 PY jX ( 0) = = 1 6 1 3 1 2
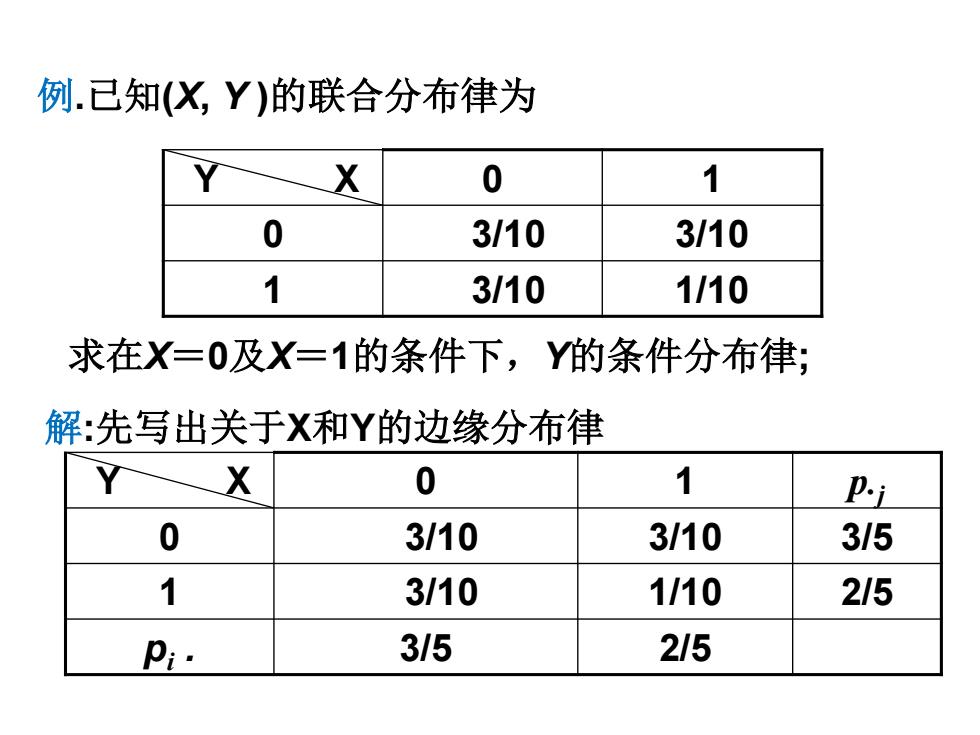
例.已知(X,Y)的联合分布律为 X 0 1 0 3/10 3/10 1 3/10 1/10 求在X=0及X=1的条件下,Y的条件分布律; 解:先写出关于X和Y的边缘分布律 Y X 0 1 卫P 0 3/10 3/10 3/5 1 3/10 1110 215 Pi. 3/5 215
例.已知(X, Y )的联合分布律为 Y X 0 1 0 3/10 3/10 1 3/10 1/10 求在X=0及X=1的条件下,Y的条件分布律; 解:先写出关于X和Y的边缘分布律 Y X 0 1 p.j 0 3/10 3/10 3/5 1 3/10 1/10 2/5 pi . 3/5 2/5

31 P{Y=0川X=0}= 10 PY=1X=0}= /10 在X=0的条件下,Y的条件分布律为 Y/X=0 0 1 P 1/2 112 同理在X=1的条件下,Y的条件分布律为 Y/X=1 0 1 Pk 3/4 1/4
在X=0的条件下,Y的条件分布律为 Y/X=0 0 1 Pk 1/2 1/2 3 10 1 { 0 | 0} , 3 2 5 PY X = = = = 3 10 1 { 1| 0} , 3 2 5 PY X = = = = 同理在X=1的条件下,Y的条件分布律为 Y/X=1 0 1 Pk 3/4 1/4

二、连续型随机变量的条件分布 设(X,)是二维连续型:v,由于对任意x,y, PX=x=0,P{Y=y}=0,所以不能直接用条件概 率公式得到条件分布
二、连续型随机变量的条件分布 设(X,Y)是二维连续型r.v,由于对任意x, y, P{X=x}=0, P{Y=y}=0 ,所以不能直接用条件概 率公式得到条件分布
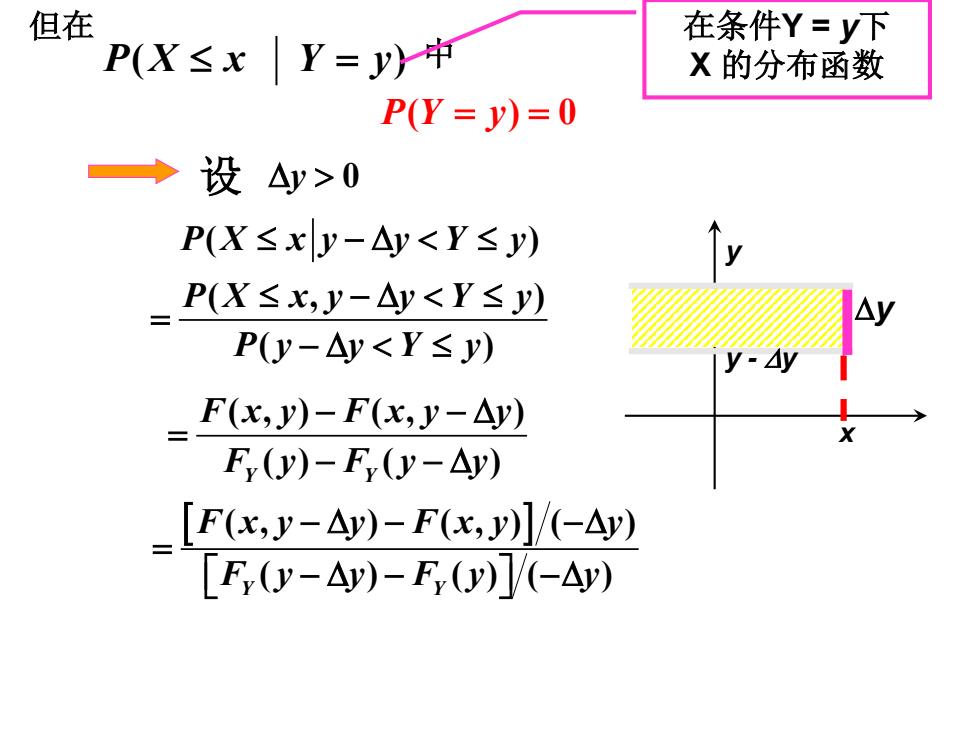
但在 在条件Y=y下 P(X≤xY=y)中 X的分布函数 P(Y=y)=0 →设△y>0 P(X≤x|y-△y<Y≤y) =PX≤x,y-4y<Y≤) P(y-△y<Y≤y) y-Ay F(x,y)-F(x,y-△y) F,y)-F(y-△y) _[F(x,y-Ay)-F(x,y)]/(-Ay) [F,(y-△y)-F,(Oy)]/(-△y)
( ) (, ) ( ) PX xy y Y y PX xy y Y y Py y Y y ≤ −∆ y 0 PY y ( )0 = = PX x Y y ( ) ≤ = 但在 中 在条件Y = y下 X 的分布函数

lim F(x,y-△y)-F(x,y)]/(-△y) △y-→0+ [F(y-△y)-F(y)]/(-△y) OF y (x,y) ["f(u,y)du d dF(y) f(y) 个 =P(X≤xY=y) y f(x,y) 连续 (y)≠0,连续
(,) ( ) Y F x y y dF y dy ∂ ∂ = (, ) ( ) x Y f u y du f y −∞ = ∫ def. = ≤= P X xY y ( ) [ ] 0 (, ) (,) ( ) lim ( ) () ( ) y Y Y Fxy y Fxy y ∆→+ Fy y Fy y − ∆ − −∆ − ∆ − −∆ (,) ( ) 0, Y f xy f y ≠ 连续 连续 (, ) ( ) x Y fuy du f y −∞ = ∫