
1.2概率 随机事件A发生可能性大小的数 值度量,称为A的概率
1.2 概率 随机事件A发生可能性大小的数 值度量,称为A的概率。 1

引例 概率起源于早期欧洲国家贵族之间盛行的赌 博问题。甲乙两个赌徒约定比赛规则为,投掷两颗骰 子,如果朝上的两个数的和为5则甲获胜,如果朝上 两个数的和为4,则乙获胜,这个规则公平吗? 2={(i,);i为第一次的点数;j为第二次的点数} ={(i2);i=1,2,.,6,j=1,2,.,6}; 2
引例 概率起源于早期欧洲国家贵族之间盛行的赌 博问题。甲乙两个赌徒约定比赛规则为,投掷两颗骰 子,如果朝上的两个数的和为5则甲获胜,如果朝上 两个数的和为4,则乙获胜,这个规则公平吗? ={( , ); } ={( , ); 1, 2,...,6; 1, 2,...,6} ij i j ij i j Ω = = 为第一次的点数; 为第二次的点数 ; 2

古典概率 设随机试验E具有下列特点: 概率的 古典定义 基本事件的个数有限 口每个基本事件等可能性发生 则称E为古典概型 古典概型中概率的计算: 记W=2中包含的基本事件总数 M=组成的基本事件个数 则 P(A-M/N
设 随机试验E 具有下列特点: 基本事件的个数有限 每个基本事件等可能性发生 则称 E 为 古典概型 古典概型中概率的计算: 记 N = Ω中包含的基本事件总数 M A = 组成 的基本事件个数 则 PA M N () / = 古典概率 概率的 古典定义 3

引例 概率起源于早期欧洲国家贵族之间盛行的赌 博问题。甲乙两个赌徒约定比赛规则为,投掷两颗骰 子,如果朝上的两个数的和为5则甲获胜,如果朝上 两个数的和为4,则乙获胜,这个规则公平吗? 令A=“点数和为4”,B=“点数和为5” P(A)= 31 3612 P(B)= 因为P(A)>P(B),甲赢的概率大
引例 概率起源于早期欧洲国家贵族之间盛行的赌 博问题。甲乙两个赌徒约定比赛规则为,投掷两颗骰 子,如果朝上的两个数的和为5则甲获胜,如果朝上 两个数的和为4,则乙获胜,这个规则公平吗? 令 A B = “点数和为4 5 ” , = “点数和为 ” 3 1 () ; 36 12 P A = = 4 1 () . 36 9 P B = = 因为 PA PB () () > ,甲赢的概率大。 4

例袋中有日只白球,b只红球,从袋中按 不放回与放回两种方式取个球, 求其中恰有k个(≤a,k≤m)白球的概率
例 袋中有a 只白球,b 只红球,从袋中按 不放回与放回两种方式取m个球, 求其中恰有 k 个 (k ≤ a,k ≤ m )白球的概率。 5

解(1)不放回情形 E:球编号,任取一球,记下颜色,放在一边, 重复m次 2:ng=Ac6)=(a+b)(a+b-1).(a+b-m+1) 记事件A为m个球中有k个白球,则 n4=C所AA- m! al b! k(m-k)!(a-k)!(b-m+k)月 则P(=C4 k≤a,k≤m 6
( )( 1) ( 1) n = A( + ) = a + b a + b − a + b − m + m Ω a b 解 (1)不放回情形 E: 球编号,任取一球,记下颜色,放在一边, 重复 m 次 W: 记事件 A 为m个球中有k个白球,则 ( )! ! ( )! ! !( )! ! b m k b a k a k m k m n C A Am k b k a k A m − + ⋅ − ⋅ − = = − 则 m a b m k b k a k m A C A A P A + − ( ) = k ≤ a,k ≤ m 6
又解E1:球编号,一次取m个球,记下颜色 21 记事件A为m个球中有k个白球,则 nA=C&C-k 因此 P(A)= k≤a,k≤m 称超几 atb 何分布 不放回地逐次取m个球,与一次任取m个 球算得的结果相同
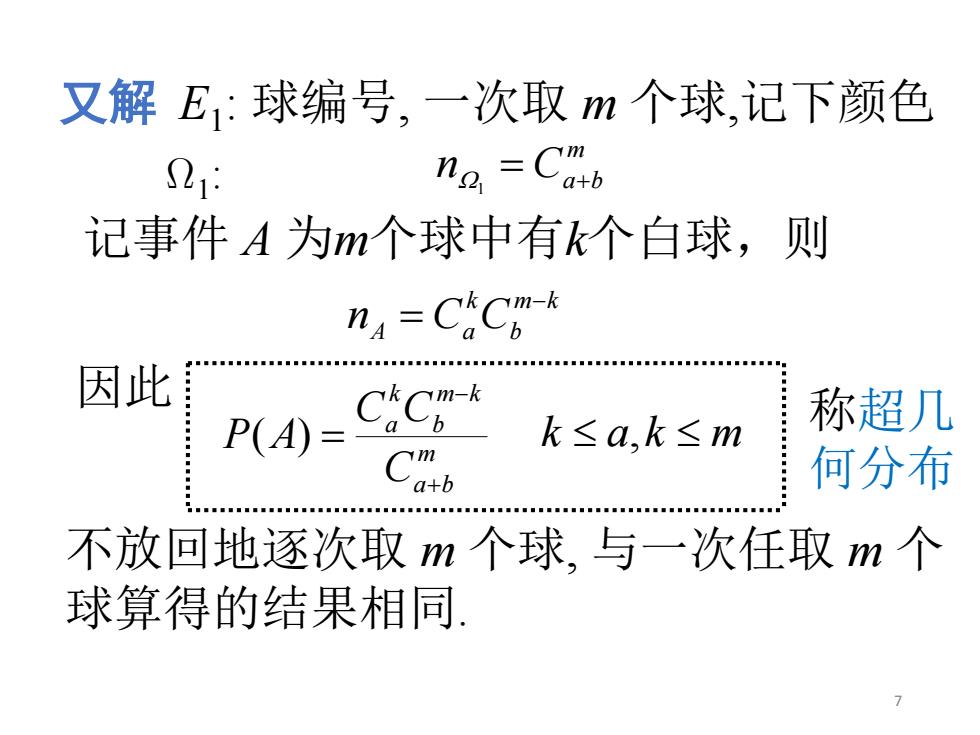
又解 E1: 球编号, 一次取 m 个球,记下颜色 m Ca b n W Ω1 = + 1: 记事件 A 为m个球中有k个白球,则 m k b k nA CaC − = 不放回地逐次取 m 个球, 与一次任取 m 个 球算得的结果相同. 因此 m a b m k b k a C C C P A + − ( ) = k ≤ a,k ≤ m 称超几 何分布 7

(2)放回情形 E2:球编号,任取一球,记下颜色,放回去, 重复m次 02 no,=(a+bym 记B为取出的m个球中有k个白球,则 Ckafb-k m-k P(B)= a (a+b)" = 记p= a+b P(B)=Chp*(1-p)"kk=1,2,..,min(a,m) 称二项分布
(2)放回情形 E2: 球编号, 任取一球, 记下颜色, 放回去, 重复 m 次 m n (a b) 2 W2 Ω = + : 记 B 为取出的 m 个球中有 k 个白球, 则 m k k m k m a b C a b P B ( ) ( ) + = − k m k k m a b b a b a C − + + = a b a p + 记 = P(B) C p (1 p) k 1,2, ,min( a,m) k k m k = m − − = 称二项分布 8

例(球入盒子模型)设有k个不同的球,每个 球等可能地落入N个盒子中(k≤),设 每个盒子容球数无限,求下列事件的概率: (1)某指定的k个盒子中各有一球: (2)某指定的一个盒子恰有m个球(m≤k) (3)某指定的一个盒子没有球: (4)恰有k个盒子中各有一球: (5)至少有两个球在同一盒子中; (6)每个盒子至多有一个球
例(球入盒子模型)设有 k 个不同的球, 每个 球等可能地落入 N 个盒子中( ), 设 每个盒子容球数无限, 求下列事件的概率: (1)某指定的 k 个盒子中各有一球; (4)恰有 k 个盒子中各有一球; (3)某指定的一个盒子没有球; (5)至少有两个球在同一盒子中; (6)每个盒子至多有一个球. (2)某指定的一个盒子恰有 m 个球( ) m k ≤ k N≤ 9

解 n Nk 设(1)~(6)的各事件分别为A→A, 则 m4= k! m4=k! P(A)= 2 m4=C(N-1)m→ P(A2)= C(N-1)-m N m4=(N-1) P(A)= (N-1 Nk ma.=Chk! P(A4)= k! Nk m,=-C一),1-m4) ma Chik! P(A)=P(A4)
解 k n N= 设 (1) ~ (6)的各事件分别为 A A 1 6 → 则 1 ! m k A = 1 1 ! ( ) A k m k P A n N = = 4 ! ( ) k N k C k P A N = 3 ( 1) ( ) k k N P A N − = 2 ( 1) ( ) m km k k C N P A N − − = 5 ! ( ) k k N k N Ck P A N − = 4 = −1 () P A 3 ( 1)k m N A = − 2 ( 1) m km m CN A k − = − 4 ! k m Ck A N = 5 ! k k m N Ck A N = − 6 ! k m Ck A N = 6 4 PA PA () () = 10