
3.5多维随机变量函数的分布 在第二章中,我们讨论了一维随机变量函数 的分布,现在我们进一步讨论: 当随机变量X1,X2,,Xn的联合分布已知时, 如何求出它们的函数 Y=gX1,X2),Xm),=1,2…,m 的分布? 我们先讨论两个随机变量的函数的分布问题, 然后将其推广到多个随机变量的情形
在第二章中,我们讨论了一维随机变量函数 的分布,现在我们进一步讨论: 我们先讨论两个随机变量的函数的分布问题, 然后将其推广到多个随机变量的情形. 当随机变量X1, X2, …,Xn的联合分布已知时, 如何求出它们的函数 Y=g(X1, X2, …,Xn), i=1,2,…,m 的分布? 3.5 多维随机变量函数的分布
一、离散型分布的情形 和的分布:Z=X+Y 例若X、Y独立,PX=)=uk,k=0,1,2,, P(Y=k)=bk,=0,1,2,…, 求Z=X+Y的概率函数. 解:P(Z=r)=P(X+Y=r) ∑P(X=i,y=r-) 由独立性 此即离散 i=0 卷积公式 ∑P(X=)PY=r- i=0 =ob,+a1b,-1+..+a,b01=0,1,2
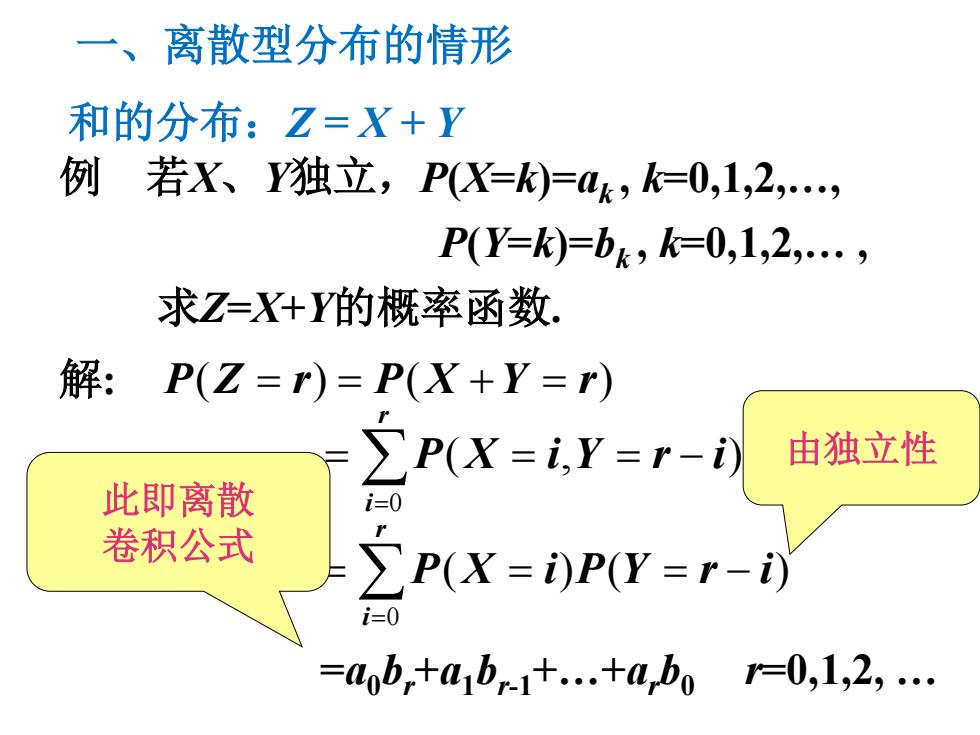
一、离散型分布的情形 例 若X、Y独立,P(X=k)=ak , k=0,1,2,…, P(Y=k)=bk , k=0,1,2,… , 求Z=X+Y的概率函数. 解: P(Z = r) = P(X +Y = r) ∑= = = = − r i P X i P Y r i 0 ( ) ( ) =a0br +a1br-1+…+arb0 ∑= = = = − r i P X i Y r i 0 ( , ) 由独立性 此即离散 卷积公式 r=0,1,2, … 和的分布:Z = X + Y

例已知随机变量(X,)的联合分布列为 1 2 3 1/5 0 1/5 2 1/5 1/5 1/5 求Z=X+Y,Z,=max{X,Y}的分布列
例 已知随机变量(X, Y)的联合分布列为 X Y 1 2 3 1 1/5 0 1/5 2 1/5 1/5 1/5 求 1 2 Z X YZ XY =+ = , max{ , }的分布列

例若X和Y相互独立,它们分别服从参数为 2,入的泊松分布, 证明Z=X+Y服从参数为 入+22的泊松分布 解:依题意 P(X=)= e2 i=0,1,2,.… 训 P(Y=j)= e j=0,1,2,… 由卷积公式 P(z=r)=∑P(x=i,Y=r-) i-0
解:依题意 ∑= = = = = − r i P Z r P X i Y r i 0 ( ) ( , ) 例 若X和Y相互独立,它们分别服从参数为 的泊松分布, 证明Z=X+Y服从参数为 1 2 λ λ, λ λ 1 2 + 的泊松分布 由卷积公式 i=0,1,2,… j=0,1,2,… ! ( ) i e P X i i 1 1 λ −λ = = ! ( ) j e P Y j j 2 2 λ −λ = =

由卷积公式 P(Z=)=∑P(X=i,Y=r-) =24e西 i=0 (r-i)川 e(+) (元1+22)',=0,1,. 即Z服从参数为人+入的泊松分布
∑= = = = = − r i P Z r P X i Y r i 0 ( ) ( , ) 由卷积公式 1 2 i r-i - - 1 2 0 e e i! (r -i)! r i λ λ λ λ = = ⋅ ∑ ∑= − + = r r i e 0 r-i 2 i 1 ( ) i!(r -i)! r! ! 1 2 λ λ λ λ ( ) , ! 1 2 ( ) 1 2 r r e λ λ λ λ = + − + 即Z服从参数为λ λ 1 2 + 的泊松分布. r=0,1,…

具有可加性的两个离散分布 口设X~B(n,p,Y~B(n2,p),且独立, 则X+Y~B(n1+n2,p) 口设X~P(1),Y~P(2),且独立, 则X+Y~P(九+2)
具有可加性的两个离散分布 设 X ~B (n1, p), Y ~B (n2, p), 且独立, 则 X + Y ~ B ( n1+n2, p) 设 X ~ P (λ1), Y ~ P (λ2), 且独立, 则 X + Y ~ P (λ1+ λ2)

二、连续型分布的情形 (1)和的分布:Z=X+Y 例设X和Y的联合密度为fx,y),求Z=X+Y的密度 解:Z=X+Y的分布函数是: F)=P(ZZ)=PXK+Y≤z) (x.yddy 这里积分区域D={化,y):x+y≤ 是直线x+y=z左下方的半平面
例 设X和Y的联合密度为 f (x,y),求Z=X+Y的密度 解: Z=X+Y的分布函数是: FZ(z)=P(Z≤z)=P(X+Y ≤ z) (, ) D = f x y dxdy ∫∫ 这里积分区域D={(x, y): x+y ≤z} 是直线x+y =z 左下方的半平面. 二、连续型分布的情形 (1) 和的分布:Z = X + Y • z • z

F(a)=∬f(x,y)drd x+y≤Z 化成累次积分,得 Fz(z)=广[frf(x,y)dr]d =∫f(x,y)dy]l fz(2)=F(a)=f(2-y,y)d 由X和Y的对称性,f(亿)又可写成 fz(2)=F2(z)=f(x,z-x)dx 以上两式是两个随机变量和的概率密度的一般公式
化成累次积分,得 () (, ) Z xyz F z f x y dxdy + ≤ = ∫∫ () [ (, ) ] z y F z f x y dx dy Z ∞ − −∞ −∞ = ∫ ∫ [ (, ) ] z y f x y dy dx − ∞ −∞ −∞ = ∫ ∫ () () ( , ) Z Z f z F z f z y y dy ∞ −∞ = = − ′ ∫ 由X和Y的对称性, fZ (z)又可写成 () () (, ) Z Z f z F z f x z x dx ∞ −∞ = = − ′ ∫ 以上两式是两个随机变量和的概率密度的一般公式

特别,当X和Y独立,设(X,)关于X,Y的边缘 密度分别为fx),fy),则上述两式化为: f(2)=[fx(z-y)/y(y)dy f(z)=fx(x)f (z-x)dx 这两个公式称为卷积公式.记为 f()=fx(a)*f(=f(a)*fx (2)
特别,当X和Y独立,设(X,Y)关于X,Y的边缘 密度分别为fX(x) , fY(y) , 则上述两式化为: () ( ) () Z XY f z f z y f y dy ∞ −∞ = − ∫ 这两个公式称为卷积公式 . 记为 () () ( ) Z XY f z f x f z x dx ∞ −∞ = − ∫ () () () () () Z XY YX fz f z fz fz f z = ∗=∗

推广:已知(X,Y)的联合密度f(xy) 求Z=aX+bY+c的密度函数, 其中a,b,c为常数,a,b≠0 a=62g- a=打r-h
推广:已知 ( X ,Y )的联合密度 f (x,y) 求 Z = aX +bY + c 的密度函数, 其中 a,b,c为常数,a , b ≠ 0 1 () , | | Z z at c f z f t dt b b +∞ −∞ − − = ∫ 1 ( ) , | | Z z bt c f z f t dt a a +∞ −∞ − − = ∫