
§2.4 随机变量的函数及其分布 问题:已知随机变量X的概率特性 分布函数或密度函数(分布列) 当 Y=8(X) 求随机因变量Y的概率特性 方法:将与Y有关的事件转化成X的事件 1
§2.4 随机变量的函数及其分布 问题:已知随机变量 X 的概率特性 —— 分布函数或密度函数(分布列) 当 Y = g ( X ) 求 随机因变量Y 的概率特性 方法:将与 Y 有关的事件转化成 X 的事件 1

一、离散型随机变量函数的概率分布 设随机变量X的分布列为 P(X=x1)=Pk, k=1,2,… 由已知函数g()可求出随机变量Y的所有 可能取值,则Y的概率分布为 P(Y=y)= ∑p, i=1,2,… k:g(xk)=yi 2
设随机变量 X 的分布列为 P(X = xk ) = pk , k =1,2, 由已知函数 g ( X) 可求出随机变量 Y 的所有 可能取值,则 Y 的概率分布为 ( ) , 1,2, : ( ) = = ∑ = = P Y y p i k i k g x y i k 一、离散型随机变量函数的概率分布 2

例1已知X的概率分布为 X -1 0 12 1 1 1 Pk 8 8 4 2 求Y=2X-1与Y2=X2的分布律 解 Y -3 -1 1 3 1 1 1 1 Pi 8 8 4 2 5
例1 已知 X 的概率分布为 X pk -1 0 1 2 2 1 4 1 8 1 8 1 求 Y 1= 2X – 1 与 Y 2= X 2 的分布律 解 Y 1 pi -3 -1 1 3 2 1 4 1 8 1 8 1 5

例(p8847题)已知X的概率分布为 P(X=k)=pg,k=012, 其中p+q=1,0<p<1, 求Y=SinX的概率分布 解pW=0)=r0x=2m =∑pm2m= 1-0 n=0
例(p88 47题) 已知 X 的概率分布为 ( ) , 0,1,2, 2 k P X k pq k π = = = 其中 p + q = 1, 0 < p < 1, 求 Y = Sin X 的概率分布 解 P Y( 0) = 0 (2 ) m 2 P Xm π ∞ = = = ⋅ 2 0 m m pq ∞ = = ∑ 2 1 p q = −

POY-1)=PU(X-2mx+ n=0 =P心x=(4m+1 00 m=0 1-4 Pr=-=PUX=2mx+】 、m=0 00 =PU(X=4m+3)) =∑pm3=,pg n=0 1-q
P Y( 1) = 0 (2 ) m 2 P Xm π π ∞ = = = + 0 ( (4 1) ) m 2 P Xm π ∞ = = = + 4 1 0 m m pq ∞ + = = ∑ 4 1 pq q = − P Y( 1) = − 0 3 (2 ) m 2 P Xm π π ∞ = = = + 0 ( (4 3) ) m 2 P Xm π ∞ = = = + 4 3 0 m m pq ∞ + = = ∑ 3 4 1 pq q = −
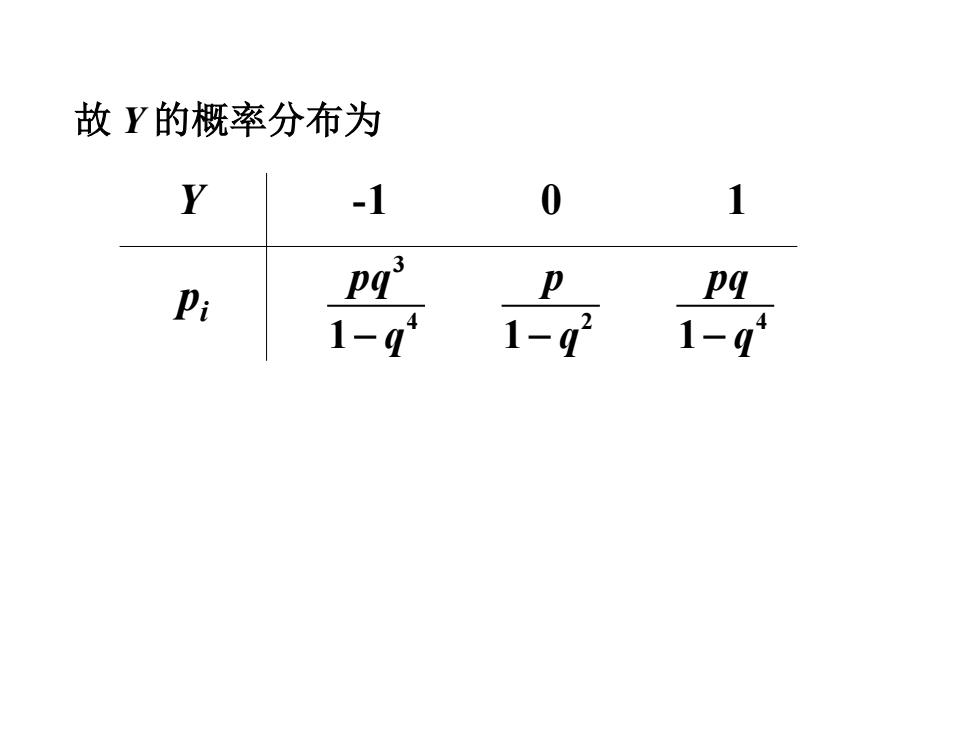
故Y的概率分布为 -1 0 Pi pqi 1-q
故 Y 的概率分布为 Y pi -1 0 1 3 424 111 pq p pq −−− qqq

二、连续型随机变量函数的分布 已知随机变量X的密度函数fx)(或分布函数) 求Y=(X)的密度函数或分布函数 方法: (1) 从分布函数出发,求出的分布函数 (2) 通过求导得密度函数 (1) 先求Y=g(X)的分布函数 F(y)=P{Y≤y以=P{g(X)≤y=∫fx(x) g(x)≤y (2)利用Y=g(X)的分布函数与密度函数之间的 关系求Y=g(X)的密度函数f(y)=FY(y): 10
已知随机变量 X 的密度函数 f (x) (或分布函数) 求 Y = g( X ) 的密度函数或分布函数 方法: (1) 从分布函数出发,求出Y的分布函数 (2) 通过求导得密度函数 二、连续型随机变量函数的分布 ⑴ 先求Y gX = ( )的分布函数 ( ) ( ) Y gX Y gX = = ⑵ 利用 的分布函数与密度函数之间的 关系求 的密度函数 F y PY y Y ( ) = ≤ { }= ≤ PgX y { ( ) } ( ) ( ) X gx y f x dx ≤ = ∫ ( ) ( ). Y Y f y Fy = ′ 10

例 设随机变量X具有概率密度: f=0, 2x,0<x<1, 其它 试求=X-4的概率密度. 解:先求Y=X-4的分布函数Fy): E,(y)=P{Y≤y} =P{X-4≤y}=P{X≤y+4} 11
2 , 0 1, ( ) 0, . X x x f x < < = 其它 设随机变量 X 具有概率密度: 试求 Y=X-4 的概率密度. 解: 先求 Y =X-4 的分布函数 FY(y): () { } F y PY y Y = ≤ 例 = −≤ = ≤+ PX y PX y { 4 } { 4} 11

F(y)=fx(x)dx. 利用F(y)=(y)可以求得: fx(X)= 2x,0<x<1, 0, 其它. f(y)=fx(y+4)×(y+4)1 2(y+4)×1,0<y+4<1, 其它 12
() () Fy f y Y Y 利用 ′ = 可以求得: ( ) ( 4) ( 4) Y X fy f y y = +×+ ′ 4 () () . y F y f x dx Y X + −∞ = ∫ < < = 0, . 2 , 0 1, ( ) 其它 x x f X X = 0 4 1, <+< y 其它. 2( 4) 1, y + × 0, 12

整理得Y=X-4的概率密度为: 2y+8,-4<y<-3, 其它 本例用到变限的定积分的求导公式 如果F)=f0dt 则 F'(x)=f[o(x)]p'(x)-f[w(x)]w'(x) 13
2 8, 4 3, ( ) 0, . Y y y f y + − < <− = 其它 整理得 Y=X-4 的概率密度为: 本例用到变限的定积分的求导公式 ( ) ( ) ( ) () , ( ) [ ( )] ( ) [ ( )] ( ). x x F x f t dt Fx f x x f x x ϕ ψ ϕϕ ψψ = ′′′ = − 如果 ∫ 则 13