
4.4矩和协方差矩阵 定义 设X和Y是随机变量,若 E0Xk),k=1,2,… 存在,称它为X的k阶原点矩,简称k阶矩 若E{[X-E(X)]},k=2,3,… 存在,称它为X的k阶中心矩 可见,均值E()是X一阶原点矩,方差D() 是X的二阶中心矩
4.4 矩和协方差矩阵 定义 设 X 和 Y 是随机变量,若 (| | ), 1, 2, k EX k = 存在,称它为 X 的 k 阶原点矩,简称 k 阶矩 若 E{[X − E(X )]k },k = 2,3, 存在,称它为 X 的 k 阶中心矩 可见,均值 E(X) 是 X 一阶原点矩,方差 D(X) 是X的二阶中心矩

设X和Y是随机变量,若 E((Xk1Y)k,L=1,2,. 存在, 称它为X和Y的k+L阶混合(原点)矩 若E{[X-E(X)][Y-E(Y)]}存在, 称它为X和Y的k+L阶混合中心矩 协方差Co(X,)是X和Y的二阶混合中心矩
协方差Cov(X,Y)是X 和Y 的二阶混合中心矩. 称它为 X 和 Y 的 k+L 阶混合(原点)矩 若 {[ ( )] [ ( )] } k L E X − E X Y − E Y 存在, 称它为X 和 Y 的 k+L 阶混合中心矩 (| | | | ) k L EX Y 设 X 和 Y 是随机变量,若 k,L=1,2,… 存在

协方差矩阵 将二维随机变量(X,X2)的四个二阶中心矩 C1=E{[X,-E(X)]2} C2=E{[X-E(X)[X2-E(X2)J} c21=E{[X2-E(X2)[X,-E(X]} c22=E{[X2-E(X2)]2} 这是一个 排成矩阵的形式: C11 C12 对称矩阵 C21 22 称此矩阵为(X,X2)的协方差矩阵
协方差矩阵 将二维随机变量(X1,X2)的四个二阶中心矩 {[ ( )] } 2 11 E X1 E X1 c = − {[ ( )][ ( )]} 12 E X1 E X1 X2 E X2 c = − − 排成矩阵的形式: {[ ( )][ ( )]} 21 E X2 E X2 X1 E X1 c = − − {[ ( )] } 2 22 E X2 E X2 c = − 称此矩阵为(X1,X2)的协方差矩阵. 11 12 21 22 c c c c 这是一个 对称矩阵

类似定义n维随机变量(X1,X2,,X)的协方差矩阵. 若c=C0v(X,Xj) =E{[X,-E(X;[X,-E(X;]} (i,j=1,2,,n) 都存在,称 矩阵 C C21 C22 Cn2 nn 为(X1,X2,,X)的协方差矩阵
类似定义n 维随机变量(X1,X2, …,Xn) 的协方差矩阵. 为 (X1,X2, …,Xn) 的协方差矩阵 都存在, ( i, j=1,2,…,n ) ( , ) i j Cov Xi X j 若 c = {[ ( )][ ( )]} = E Xi − E Xi X j − E X j = n n nn n n c c c c c c c c c C 1 2 21 22 2 11 12 1 矩阵 称

维正态分布的概率密度 设X'=(XX2,,X)是一个n维随机向量, 若它的概率密度为 fW)F2o1c阳exp2(X-4yC'(X-w} 则称X服从n维正态分布. 其中C是(X1,X2,…X,)的协方差矩阵. C是它的行列式,C表示C的逆矩阵, X和是n维列向量,X'表示X的转置
n 维正态分布的概率密度 ( ) ( )} 2 1 exp{ (2 ) | | 1 1 2 1 2 µ µ π = − − ′ − − X C X C n f (x1,x2, …,xn) 则称 X 服从 n 维正态分布. 其中C是(X1,X2, …,Xn) 的协方差矩阵. |C|是它的行列式,C−1 表示C的逆矩阵, X 和 µ是 n 维列向量,X′表示X 的转置. 设 =(X1,X2, …,Xn) 是一个n维随机向量, 若它的概率密度为 X′
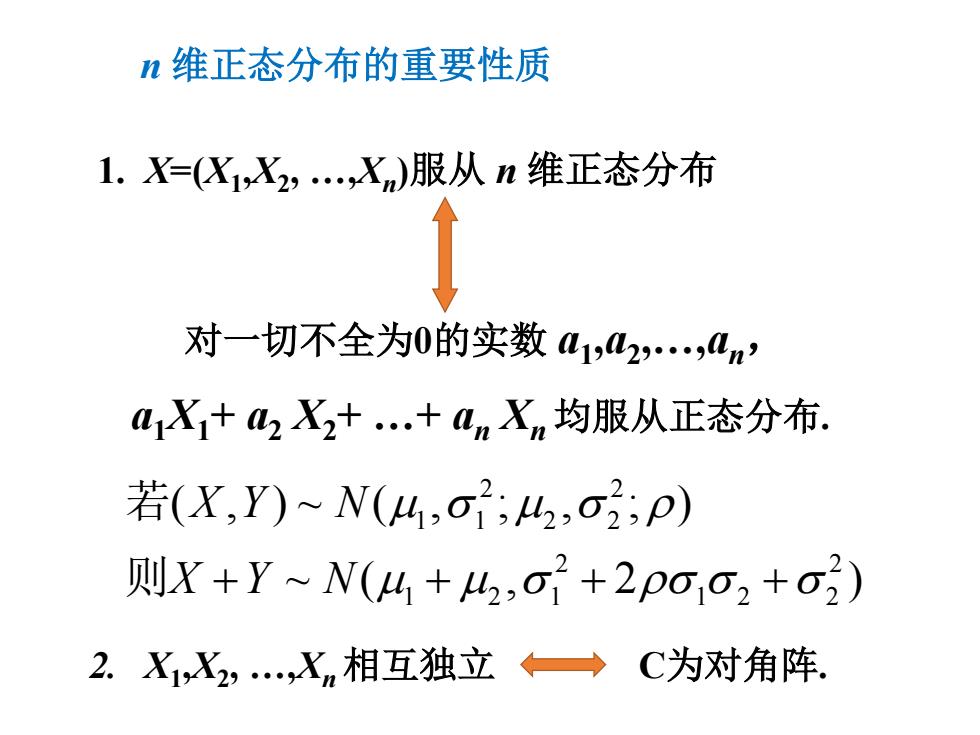
n维正态分布的重要性质 1.X=(X,X,,X)服从n维正态分布 对一切不全为0的实数01,42,0n’ 1X+2X2+.+nXn均服从正态分布. 若(X,Y)~N(4,o;42,02P) 则X+Y~N(4+42,o2+2po02+o2) 2.X1,X2,…,Xn相互独立→C为对角阵
n 维正态分布的重要性质 1. X=(X1,X2, …,Xn)服从 n 维正态分布 a1X1+ a2 X2+ …+ an Xn 均服从正态分布. 对一切不全为0的实数 a1,a2,…,an, 2. X1,X2, …,Xn 相互独立 C为对角阵. 2 2 11 2 2 2 2 1 2 1 12 2 ( , )~ ( , ; , ; ) ~( , 2 ) XY N XY N µσ µσ ρ + ++ + µ µ σ ρσ σ σ 若 则