
4.2方差 引例检验两批灯泡的质量,从中分别随机抽样5只, 测得使用寿命(单位:小时)如下: A:20001500 1000 500 1000 B:15001500 10001000 1000 试比较这两批灯泡质量的好坏 计算得:平均寿命分别为:A:1200B:1200 数学期望 方差 观察得:A中使用寿命偏离较大,B中使用寿命 偏离较小,所以,B产品质量较好
4.2 方差 引例 检验两批灯泡的质量,从中分别随机抽样5只, 测得使用寿命(单位:小时)如下: A: 2000 1500 1000 500 1000 B: 1500 1500 1000 1000 1000 试比较这两批灯泡质量的好坏 计算得:平均寿命分别为:A:1200 B:1200 观察得:A中使用寿命偏离较大,B中使用寿命 偏离较小,所以,B产品质量较好 数学期望 方差

1.方差的定义 定义:设X是一个随机变量,若E(X-EX)2存在 则称E(X-EX)2为X的方差,记为DX,即 方差 DX=E(X-EX) 均方差(标准差)ox=VDX (X-EX)2— 随机变量X的取值偏离平均值的 情况,是X的函数,也是随机变量 EX-EX)2一随机变量X的取值偏离平均值 的平均偏离程度—数 注:方差反映了随机变量相对其均值的偏离程度
2 2 ,( ) , () , , X E X EX E X EX X DX − − 设 是一个随机变量 若 存在 则称 为 的方差 记为 即 1. 方差的定义 (X - EX)2 —— 随机变量X 的取值偏离平均值的 情况, 是X的函数, 也是随机变量 E(X - EX)2 —— 随机变量X的取值偏离平均值 的平均偏离程度—— 数 定义: 2 方差 DX E X EX = − ( ) ( ) 均方差 标准差 σ X = DX 注: 方差反映了随机变量相对其均值的偏离程度

若X为离散型随机变量,概率分布为 P(X=Xk)=pk,k=1,2,… DX=∑(x&-EX}P 若X为连续型随机变量,概率密度为f(x) DX=∫(x-EX}f(x)d 常用的计算方差的公式: DX=EX2-(EX)
P(X = xk ) = pk , k = 1,2, 若 X 为离散型随机变量,概率分布为 = ∑( − ) k k k DX x EX p 2 若 X 为连续型随机变量,概率密度为f (x) DX (x EX) f (x)dx 2 ∫ +∞ −∞ = − 常用的计算方差的公式: 2 2 DX EX EX = − ( )
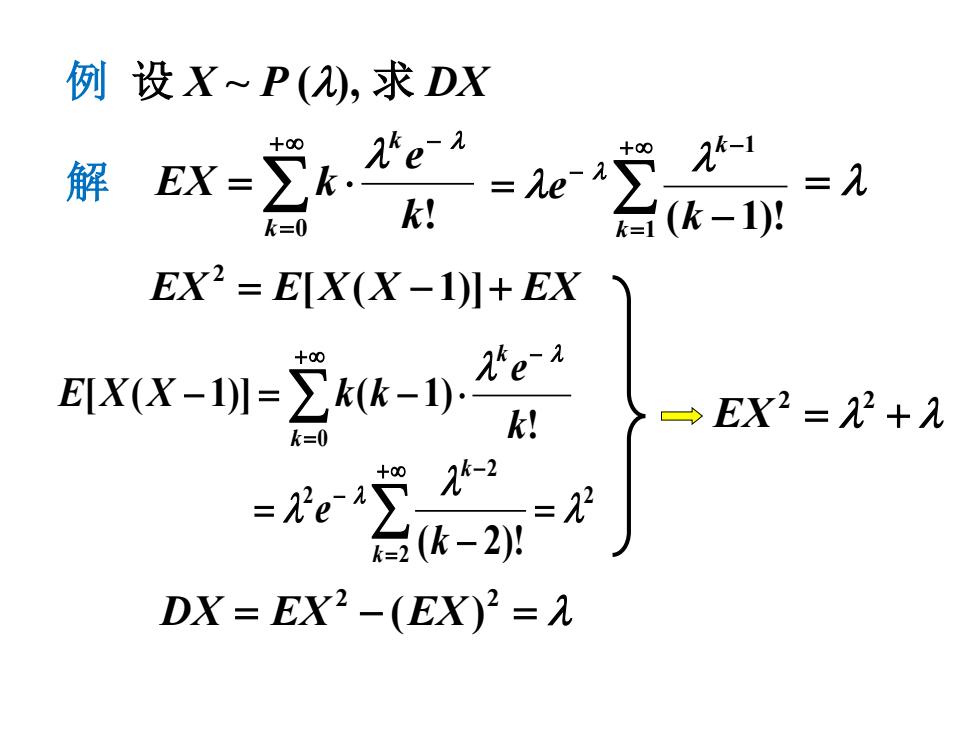
例设X~P(2),求DX +0 解 EX= . 2-1 =见 k=0 k! 台(k-1)月 EX2=EX(X-1)川+EX XX-叨=kk-). 十00 →EX2=22+孔 k=0 +0 =e 1-2 =12 k-2 DX=EX2-(EX)2=入
例 设 X ~ P (λ), 求 DX 解 ∑ +∞ = − = ⋅ 0 ! k k k e EX k λ λ ∑ +∞ = − − − = 1 1 ( 1)! k k k e λ λ λ = λ EX = E[X(X − 1)]+ EX 2 ! [ ( 1)] ( 1) 0 k e E X X k k k k λ λ +∞ − = − = ∑ − ⋅ 2 2 2 2 ( 2)! λ λ λ λ = − = ∑ +∞ = − − k k k e = λ + λ 2 2 EX = − = λ 2 2 DX EX (EX)

例设X~U(a,b),求DX 解DX=EX2-(EX)2 ='-( (b-a)2 12
解 DX 2 2 = − EX EX ( ) 2 2 1 ( ) 2 b a a b x dx b a + = − − ∫ 2 ( ) 12 b a − = 例 设 X ~ U( a , b),求 DX

例设X~N(4,σ2),求DX 第=。罗。 202 dx =02
例 设 X ~ N ( µ , σ 2), 求 DX 解 DX x e dx x 2 2 2 ( ) 2 2 1 ( ) σ µ πσ µ − +∞ − ∫ −∞ = − t e dt t t x 2 2 2 2 2 +∞ 1 − −∞ = − ∫ = π σ σ µ 令 2 = σ

例假设某品牌热水器的寿命服从参数为2的指 数分布,为安全起见,厂家建议热水器用到第 m年要被淘汰(m为一正常数),否则会有一 些安全隐患。如果用户按照厂家的建议年即 淘汰热水器,那么对于用户来讲热水器寿命的 平均值和方差各是多少? 解设热水器的寿命用X表示,对用户来讲热水器寿 命用Y表示,根据题意Y=min{X,m} 根据假设X的概率密度为: Ae, x>0 f(x)= 0, x≤0
例 假设某品牌热水器的寿命服从参数为λ的指 数分布,为安全起见,厂家建议热水器用到第 m年要被淘汰(m为一正常数),否则会有一 些安全隐患。如果用户按照厂家的建议m年即 淘汰热水器,那么对于用户来讲热水器寿命的 平均值和方差各是多少? 解 设热水器的寿命用 X 表示,对用户来讲热水器寿 命用 Y 表示,根据题意 Y m Xm = in{ , } 根据假设 X 的概率密度为: , 0 ( ) 0, 0 x e x f x x λ λ − > = ≤
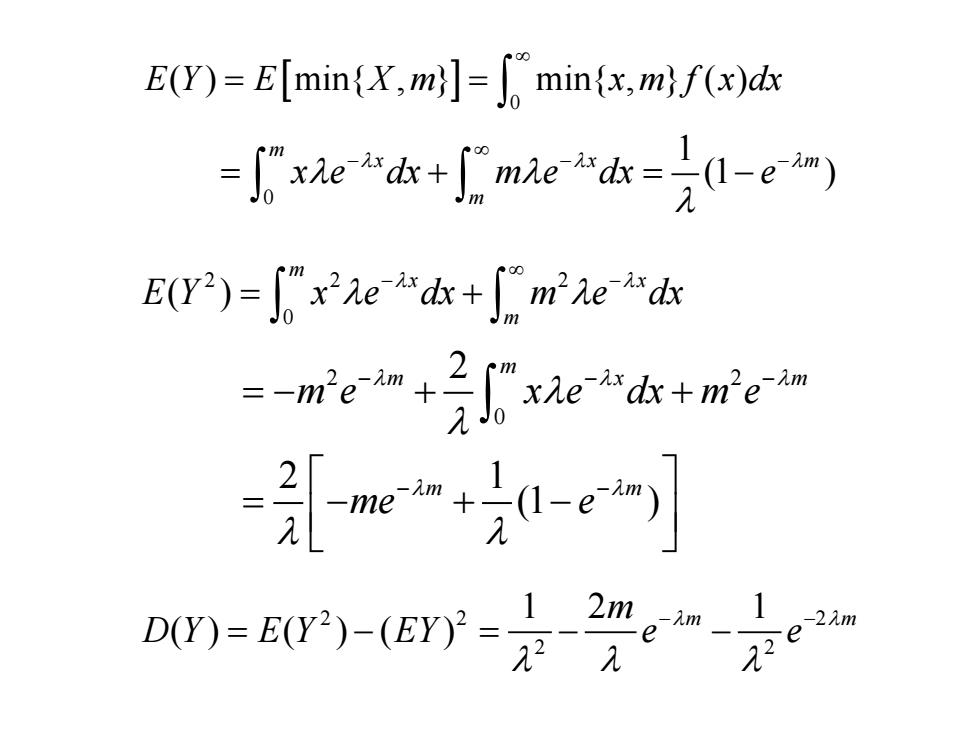
E(Y)=E[min{X,m]=min{x,m)f(x)dx -e“dk+me“ak=2l-e) E(Y2)=xr2aedk+∫m2e“dk 引“+0e D(Y)=E(Y)-(Er)= 2m 2m 12 e
[ ] 0 E Y E X m x m f x dx ( ) min{ , } min{ , } ( ) ∞ = = ∫ 0 1 (1 ) m xx m m x e dx m e dx e λλ λ λ λ λ ∞ −− − = + =− ∫ ∫ 22 2 0 ( ) m x x m E Y x e dx m e dx λ λ λ λ ∞ − − = + ∫ ∫ 2 2 0 2 2 1 (1 ) m m xm m m m e x e dx m e me e λ λλ λ λ λ λ λ λ − −− − − =− + + =− + − ∫ 2 2 2 2 2 12 1 () ( ) ( ) m m m D Y E Y EY e e λ λ λλ λ − − = − =− −

2.方差的性质 (I)D(X)存在台E(X2)<+o (2)D(C)=0(C为常数) (3)D(CX)=C2D(X) (4)设X,Y是两个相互独立的随机变量,则 D(X±Y)=DX+DY 推广:X,…,Xn相互独立,D(X,)存在,则 D2X,)=2D(X,》
2. 方差的性质 (2) 0 ( DC C ( )= 为常数) 2 (3) ( ) D CX C D X = ( ) 1 1 1 (4) , , ( ) , , ( ) ( ) () n i n n i i i i X Y D X Y DX DY X X DX D X DX = = ±= + ∑ ∑= 设 是两个相互独立的随机变量 则 推广: 相互独立, 存在,则 2 (1) ( ) (| | ) DX E X 存在 ⇔ < +∞

(5) D(X)=E(X-a)2)-(E(X)-a)2 (a为任意常数) (6)D(X)≤E(X-a)2)(a为任意常数) (7)D(X)=0的充要条件是X以概率1取常数C (这里C=E(X),即P(X=C)=1
(7) ( ) 0 1 ( ( )) , ( ) 1 D X X C C EX PX C = = = = 的充要条件是 以概率 取常数 这里 即 2 2 (5) ( ) (( ) ) ( ( ) ) ( ) DX E X a EX a a = −− − 为任意常数 2 (6) ( ) (( ) ) ( DX E X a a ≤ − 为任意常数)