
第七章参数佑计
第七章 参数估计

什么是参数估计? 参数是刻画总体某方面的概率特性的数量, 当这个数量是未知的时候,从总体抽出一个 样本,用某种方法对这个未知参数进行估计 就是参数估计. 例如,X~N(4,σ2), 若4ō2未知,通过构造样本的函数,给出它 们的估计值或取值范围就是参数估计的内容 点估计 区间估计
什么是参数估计? 参数是刻画总体某方面的概率特性的数量. 当这个数量是未知的时候,从总体抽出一个 样本,用某种方法对这个未知参数进行估计 就是参数估计. 例如,X ~N (µ ,σ 2), 点估计 区间估计 若µ, σ 2未知,通过构造样本的函数, 给出它 们的估计值或取值范围就是参数估计的内容

参数估计的类型 点估计(point Estimation)一估计未知参数的值 区间估计(interval Estimation)一 估计未知参数的 取值范围,使得这个范围包含未知参数真值的 概率为给定的值
参数估计的类型 点估计(point Estimation) —— 估计未知参数的值 区间估计(interval Estimation)—— 估计未知参数的 取值范围,使得这个范围包含未知参数真值的 概率为给定的值

7.1点估计法 点估计的思想方法 设总体X的分布函数的形式已知,但它含有 一个或多个未知参数:0,02,,0 设X,X2,,X,为总体的一个样本 构造k个统计量: 0(X1,X2,…,Xn) 02(X1,X2,…,Xn) 随机变量 0(X1,X2,…,Xn)
7.1 点估计法 点估计的思想方法 设总体X 的分布函数的形式已知,但它含有 一个或多个未知参数:θ1,θ2, …,θk 设 X1, X2,…, Xn为总体的一个样本 构造 k 个统计量: ( , , , ) ( , , , ) ( , , , ) 1 2 2 1 2 1 1 2 k n n n X X X X X X X X X θ θ θ 随机变量
当测得一组样本值化1,x2,x)时,代入上述 统计量,即可得到k个数: 01(x1,x2,…,xn) 02(x1,x2,…,xn) 数值 0(x1,x2,…,xn) 称数0,,…,0为未知参数0,02,…,0.的估计值 对应的统计量为未知参数0,02,…,O的估计量 Q:如何构造统计量? 如何评价估计量的好坏?
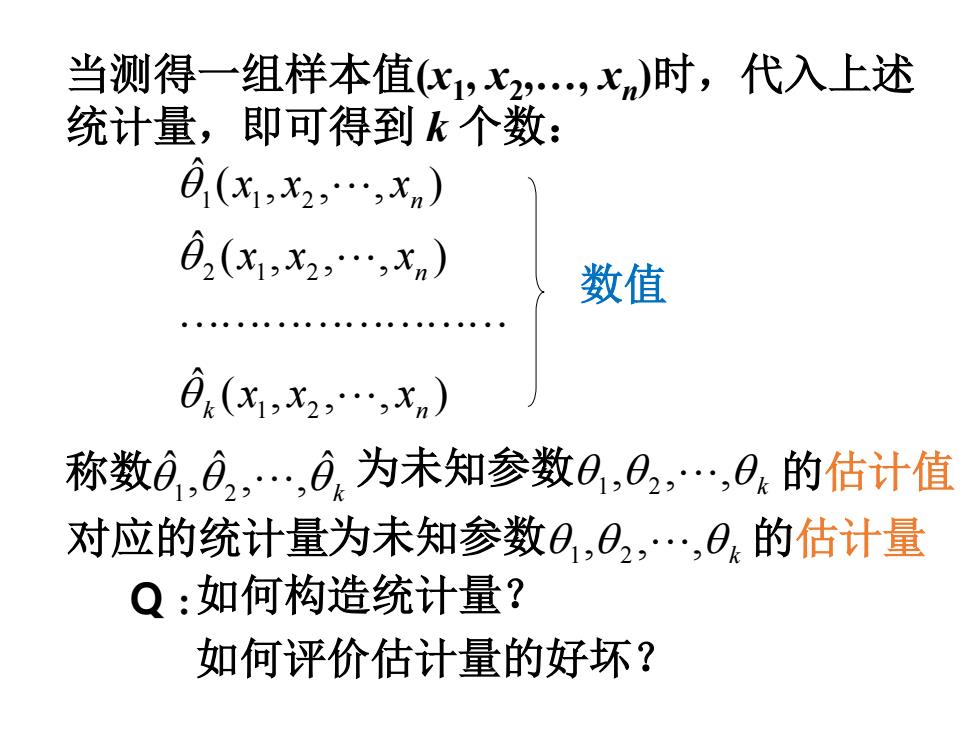
当测得一组样本值(x1, x2,…, xn)时,代入上述 统计量,即可得到 k 个数: ( , , , ) ˆ ( , , , ) ˆ ( , , , ) ˆ 1 2 2 1 2 1 1 2 k n n n x x x x x x x x x θ θ θ 数值 称数θ θ θ k ˆ , , ˆ , ˆ 1 2 为未知参数θ θ θ k , , , 1 2 的估计值 如何构造统计量? 如何评价估计量的好坏? 对应的统计量为未知参数θ θ θ k , , , 1 2 的估计量 Q :

常用的点估计方法 口频率替换法 利用事件A在n次试验中发生频率 n 作为事件A发生的概率D的估计量 卫 n
常用的点估计方法 频率替换法 利用事件A 在 n 次试验中发生频率 n nA 作为事件A 发生的概率 p 的估计量 p n nA p →

例1设总体X~N(4,2),在对其作28次独立 观察中,事件“X<4”出现了21次,试用频率替 换法求参数的估计值, 释由P<4E02≈207万 28 查表得 4-4=0.675 V2 于是的估计值为d≈3.045
例1 设总体X ~ N ( µ , 2 ), 在对其作28 次独立 观察中, 事件 “X < 4”出现了21 次, 试用频率替 换法求参数 µ的估计值. 解 由 0.75 28 21 ) 2 4 ( 4) ( ≈ = − < = Φ µ P X 0.675 2 4 = − µ 查表得 于是 µ的估计值为 ∧ µ ˆ ≈ 3.045

口矩估计法 用样本的k阶矩作为总体的k阶矩的 方法 估计量,建立含有待估计参数的方程, 从而可解出待估计参数
矩估计法 方法 用样本的 k 阶矩作为总体的 k 阶矩的 估计量, 建立含有待估计参数的方程, 从而可解出待估计参数

设待估计的参数为0,02,…,0 设总体的r阶矩存在,记为 E(X)=4,(0,02,…,0k) 设X,X2,Xn为一样本,样本的r阶矩为 B.-X 应 i=1 4.(0,02,…,0)=2Xr=1,2,,k n i=l 含未知参数日,0,,9的方程组
设待估计的参数为θ θ θ k , , , 1 2 设总体的 r 阶矩存在,记为 ( ) ( , , , ) r 1 2 k r E X = µ θ θ θ 设 X1, X2,…, Xn为一样本,样本的 r 阶矩为 ∑ = = n i r r Xi n B 1 1 r =1,2,,k 令 ( , , , ) µr θ1 θ 2 θ k ∑= = n i r Xi n 1 1 —— 含未知参数 θ1,θ2, …,θk 的方程组
解方程组,得k个统计量: (X1,X2,…,Xn) 02(X1,X2,…,Xm) 未知参数0,02,…,0k 的矩估计量 0(X1,X2,…,Xn) 代入一组样本值得k个数: 61=01(x1,x2,…,xm) 62=02(x1,x2,…,xn) 未知参数0,02,,0 的矩估计值 6=0%(c1,x2,…,xn)
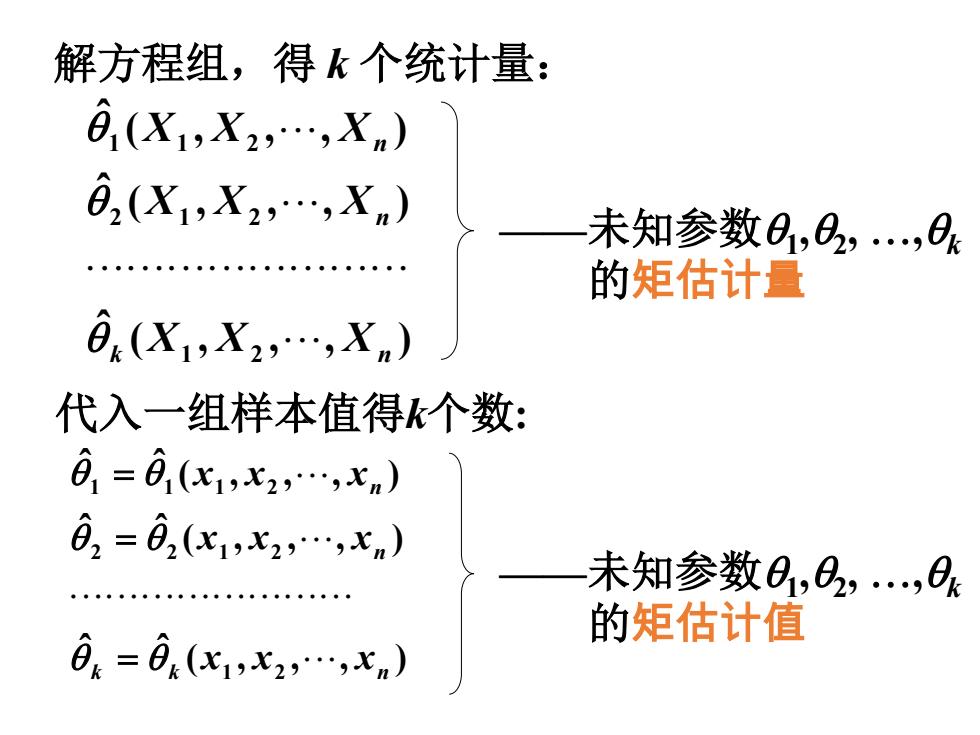
解方程组,得 k 个统计量: ( , , , ) ˆ ( , , , ) ˆ ( , , , ) ˆ 1 2 2 1 2 1 1 2 k n n n X X X X X X X X X θ θ θ ——未知参数θ1,θ2, …,θk 的矩估计量 ( , , , ) ˆ ˆ ( , , , ) ˆ ˆ ( , , , ) ˆ ˆ 1 2 2 2 1 2 1 1 1 2 k k n n n x x x x x x x x x θ θ θ θ θ θ = = = ——未知参数θ1,θ2, …,θk 的矩估计值 代入一组样本值得k个数: