
线性代数教学参考书 刘剑平 2006年9月 前言 课程介绍 背景 线性代数是代数的一个分支,由于费马和笛卡儿的工作而起源于十七什纪,线性代数是 研究有限维空间中线性关系的理论和方法的数学。线性代数课程在高等工业学校的教学计划 中是一门基础理论课,也是一门研究生入学考试的必考课程。由于线性问题广泛存在于技 科学的各个领域,某些非线性问题在一定条件下可以转化为线性问题,而且无限维的问题也 常“离散化”为有限维问题来处理,因此线性代数的理论与方法已经渗透到现代科学、技术、 经济、管理的各个领域,提供描述、处理问颗的思想和方法。随若科学技术数学化和计算机 的广泛应用,线性代数在现代科技和高等教有中的地位和作用愈显重要,尤其在计算机日益 普及的今天,解决大型线性方程组 、求矩阵的特征值与特征向量等已经成为工程人员常遇到 的课题,因此木课程所介绍的方法广泛地应用各个学科,尤其在计算机、通讯、电子等学科 领域,这就要求学生具有关于本课程地基础知识,并熟练地掌捏它地方法。 培养目的 线性代数是以讨论有限维空间线性理论为主的课程,具有较强地抽象性与逻辑性。通过 本课程地学习,使学生掌握线性代数地基本理论和基本方法,使学生获得应用科学中常用地 矩阵方法、线性方程组、二次型等理论及其有关基木知识,并具有熟练地矩阵运算能力和用 矩阵方法解决一些实际问题的能力,并在抽象思维和逻辑推理能力方面得到一定地训练,提 高分析和解决问题的能力,培养科学思维和创新能力,从而为学习后继课程及进一步扩大数 学知识面莫定必要的数学基础。 学习方法 本课程定义、定理等概念比较多,由一定地抽象性,且有一套独特地理论体系和处理问 题的规律和方法。因此,有一定地学习难度。要学好,除了重视书本的学习,认其阅读教材 以外,做一定量的课外练习也是必不可少的,参考书的合理使用是行之有效的。只有在阅读 的基础上加以练习,才能加深对概念的理解和方法的掌握,从而获得相关的知识,进一步提 高逻辑思维能力。 课程的重点、难点 木课程的重点句括:矩阵的定义和运算:逆矩阵的求解:矩阵方程的求解:矩阵的初等 变换:行列式的定义和性质:行列式按行(列)展开定理 的计 克莱姆法则: 阵的秩的定义和计算:线性方程组的求解:向量组的线性关系:相似矩阵的定义和求解 木课程的难点包括:逆矩阵的求解:矩阵的初等变换:高阶行列式的计算:线性方程组 的求解:向最组的线性关系:相似矩阵的求解。 PDF文件使用"pdfFactory Pro”试用版本创建w,fineprint,cn
线性代数教学参考书 刘剑平 2006 年 9 月 前言 课程介绍 背景 线性代数是代数的一个分支,由于费马和笛卡儿的工作而起源于十七世纪,线性代数是 研究有限维空间中线性关系的理论和方法的数学。线性代数课程在高等工业学校的教学计划 中是一门基础理论课,也是一门研究生入学考试的必考课程。由于线性问题广泛存在于技术 科学的各个领域,某些非线性问题在一定条件下可以转化为线性问题,而且无限维的问题也 常“离散化”为有限维问题来处理,因此线性代数的理论与方法已经渗透到现代科学、技术、 经济、管理的各个领域,提供描述、处理问题的思想和方法。随着科学技术数学化和计算机 的广泛应用,线性代数在现代科技和高等教育中的地位和作用愈显重要,尤其在计算机日益 普及的今天,解决大型线性方程组、求矩阵的特征值与特征向量等已经成为工程人员常遇到 的课题,因此本课程所介绍的方法广泛地应用各个学科,尤其在计算机、通讯、电子等学科 领域,这就要求学生具有关于本课程地基础知识,并熟练地掌握它地方法。 培养目的 线性代数是以讨论有限维空间线性理论为主的课程,具有较强地抽象性与逻辑性。通过 本课程地学习,使学生掌握线性代数地基本理论和基本方法,使学生获得应用科学中常用地 矩阵方法、线性方程组、二次型等理论及其有关基本知识,并具有熟练地矩阵运算能力和用 矩阵方法解决一些实际问题的能力,并在抽象思维和逻辑推理能力方面得到一定地训练,提 高分析和解决问题的能力,培养科学思维和创新能力,从而为学习后继课程及进一步扩大数 学知识面奠定必要的数学基础。 学习方法 本课程定义、定理等概念比较多,由一定地抽象性,且有一套独特地理论体系和处理问 题的规律和方法。因此,有一定地学习难度。要学好,除了重视书本的学习,认真阅读教材 以外,做一定量的课外练习也是必不可少的,参考书的合理使用是行之有效的。只有在阅读 的基础上加以练习,才能加深对概念的理解和方法的掌握,从而获得相关的知识,进一步提 高逻辑思维能力。 课程的重点、难点 本课程的重点包括:矩阵的定义和运算;逆矩阵的求解;矩阵方程的求解;矩阵的初等 变换;行列式的定义和性质;行列式按行(列)展开定理;行列式的计算;克莱姆法则;矩 阵的秩的定义和计算;线性方程组的求解;向量组的线性关系;相似矩阵的定义和求解。 本课程的难点包括:逆矩阵的求解;矩阵的初等变换;高阶行列式的计算;线性方程组 的求解;向量组的线性关系;相似矩阵的求解。 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

教学内容和教学安排 以线性方程组的求解为核心展开矩阵、行列式等基本概念的讨论,进而解决线性方程组 的求解:同时,为了引出线性方程组解的结构,讨论了问量空间:最后,讨论了用途极广的 特征问题及二次型。 先讲矩阵是因为矩阵是线性代数的基础,一切代数运算归根到底是矩阵的运算,同时,讲行列 式也丰富了许多:先讲线性方程组的求解后讲向量空间是为了将抽象的向量关系用具体的线性方程 组的求解来解释,以便学生很好地理解概念。 教材:《线性代数》,刘剑平、施劲松、曹宵临主编华东理工大学出版社,2003 《线性代数》电子教材,刘剑平主编华东理工大学出版社,2004 《工程数学》,刘剑平、施劲松、陆元鸿主编,华东理工大学出版社,2003 参考书:《线性代数精析与精练》,刘剑平、曹肖临主编,华东理工大学出版社,2004 《线性代数复习与解题指导》,刘剑平、曹宵临主编,华东理工大学出版社,2001 《工程数学习题解答与复习指南》,刘剑平等主编,华东理工大学出版社,2003 教学的基本内容安排 (一)矩阵(11学时) 1.矩阵的概念 2.矩阵的运算 3.逆矩阵 4.矩阵的分块 5.初等变换与初等矩阵 (二)行列式(9学时) 1.行列式的定义 2.n阶行列式的展开公式 3.行列式的性质 PDF文件使用”pdfFactory Pro”试用版本创建ww,fineprint.cn
教学内容和教学安排 以线性方程组的求解为核心展开矩阵、行列式等基本概念的讨论,进而解决线性方程组 的求解;同时,为了引出线性方程组解的结构,讨论了向量空间;最后,讨论了用途极广的 特征问题及二次型。 先讲矩阵是因为矩阵是线性代数的基础,一切代数运算归根到底是矩阵的运算,同时,讲行列 式也丰富了许多;先讲线性方程组的求解后讲向量空间是为了将抽象的向量关系用具体的线性方程 组的求解来解释,以便学生很好地理解概念。 教 材:《线性代数》,刘剑平、施劲松、曹宵临主编 华东理工大学出版社,2003 《线性代数》电子教材,刘剑平主编 华东理工大学出版社,2004 《工程数学》,刘剑平、施劲松、陆元鸿主编,华东理工大学出版社,2003 参 考 书:《线性代数精析与精练》,刘剑平、曹宵临主编,华东理工大学出版社,2004 《线性代数复习与解题指导》,刘剑平、曹宵临主编,华东理工大学出版社,2001 《工程数学习题解答与复习指南》,刘剑平等主编,华东理工大学出版社,2003 教学的基本内容安排 (一) 矩阵(11 学时) 1.矩阵的概念 2.矩阵的运算 3.逆矩阵 4.矩阵的分块 5.初等变换与初等矩阵 (二) 行列式(9 学时) 1.行列式的定义 2.n 阶行列式的展开公式 3.行列式的性质 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

4.行列式的计算 5.行列式的应用 (三)矩阵的秩和线性代数方程组(9学时) 1.矩阵的秩 2。齐次线性方程组 3.非齐次线性方程组 (四)向量空间(11学时) 1.向量的线性相关与线性无关 2.向量组的秩 3.向量空间 4,线性方程组解的结构 5.向量的内积 (五)特征值问题与二次型(12学时) 1.方阵的特征值与特征向量 2。相似矩阵 3.实对称矩阵的对角化 4.二次型及其标准形 5.正定二次型与正定矩阵 机动(2学时) 注:(36学时到四2止) 第一章 1.1基本内容 PDF文件使用"pdfFactory Pro”试用版本创建,fineprint,cn
4.行列式的计算 5. 行列式的应用 (三) 矩阵的秩和线性代数方程组(9 学时) 1.矩阵的秩 2.齐次线性方程组 3.非齐次线性方程组 (四) 向量空间(11 学时) 1.向量的线性相关与线性无关 2.向量组的秩 3.向量空间 4.线性方程组解的结构 5. 向量的内积 (五)特征值问题与二次型(12 学时) 1.方阵的特征值与特征向量 2.相似矩阵 3.实对称矩阵的对角化 4.二次型及其标准形 5. 正定二次型与正定矩阵 机动(2 学时) 注:(36 学时到四 2 止) 第一章 1.1 基本内容 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

11.1矩阵的概老 (1)定义 由m×n个元素a,=1,2,,m,j=1,2,…,n)排成的m行,n列的矩阵元素表 [ala2…an dm d2…am 称为维是m×n的矩阵,简记为A=a,) 注1本书中我们时论的主要是实矩阵,即A的元素a,为实数的情形。 注2当m=n时,称A为n阶方阵。 注3称An与B为同维(阶)矩阵,如果两个同维矩阵A与B的对应元素相等,则A B (2)特殊矩阵 零矩阵:元素全为零的矩阵,记作0 行矩阵:A=[4,a2,…,an] a 列矩阵:A=9, a。 au an...am 三角阵:A= a…a2m 称为上三角,满足a=0(>) 00…am a10 0 B= a21a2…0 称为下三角,满足a。=01<) 2… PDF文件使用”pdfFactory Pro”试用版本创建,fineprint,cn
1.1.1 矩阵的概念 (1)定义 由 m´ n 个元素 a (i m j n) ij = 1,2,L, ; = 1,2,L, 排成的 m 行,n 列的矩阵元素表 ú ú ú ú ú û ù ê ê ê ê ê ë é = m m mn n n a a a a a a a a a A L L L L L 1 2 21 22 2 11 12 1 称为维是 m´ n 的矩阵,简记为 ( ) m n A aij ´ = 。 注1 本书中我们讨论的主要是实矩阵,即 A 的元素 aij 为实数的情形。 注2 当 m = n时,称 A 为 n 阶方阵。 注3 称 Am´n 与 Bm´n 为同维(阶)矩阵,如果两个同维矩阵 A 与 B 的对应元素相等,则 A =B。 (2)特殊矩阵 零矩阵:元素全为零的矩阵,记作 0 行矩阵: [ ] n A a , a , ,a = 1 2 L 列矩阵: ú ú ú ú û ù ê ê ê ê ë é = an a a A M 2 1 三角阵: A = ú ú ú ú ú û ù ê ê ê ê ê ë é mn n n a a a a a a L M M O M L L 0 0 0 22 2 11 12 1 称为上三角,满足 a (i j) ij = 0 > ú ú ú ú ú û ù ê ê ê ê ê ë é = m m mn a a a a a a B L M M O M L L 1 2 21 22 11 0 0 0 称为下三角,满足 a (i j) ij = 0 < PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

[a0…0 对角阵:A= 0a2…0 diag(an,a2n,…am) 00…a 「k 数量阵:diag(k,k,…k)= k 入 1 单位阵:diag(L,…)= 常记作In或I,有时也记作En或E。 1 对称阵:A=A「 反对称阵:A=一A 注1行(列)矩阵通常称为行(列)向量。并习惯用小写字母表示,其每一元素称为分量。 分量个数称为维数。 注2上述所列的特殊矩阵,除零矩阵、行或列矩阵外,均为方阵。 注3对反对称阵A=Qg)来说,必有a。=0(=1,2…n)。 注4任一方阵A均可表示为一个对称阵和一个反对称阵之和,即 A=4+4)+-) 11.2矩阵的运算 (1)加法:设A=a,),B=6,)m,则A+B=a,+b,) (2)数承:设A=by)k为数,则M=a,)n (3)乘法:设A=(a,)'B=b,)n,则AB=e,)n,其中 C,=aby=a4y+ab,+…a.b,6=l2.…mj=l2.n) 注两矩阵可乘的条件:左边矩阵的列数等于右边矩阵的行数。 PDF文件使用"pdfFactory Pro”试用版本创建w,fineprint,cn
对角阵: ( ) nn mn diag a a a a a a A L L M M O M L L , , 0 0 0 0 0 0 11 22 22 11 = ú ú ú ú ú û ù ê ê ê ê ê ë é = 数量阵: ( ) ú ú ú ú û ù ê ê ê ê ë é = k k k diag k k k O , ,L 单位阵: ( ) ú ú ú ú û ù ê ê ê ê ë é = 1 1 1 1,1, 1 O diag L ,常记作 n I 或 I ,有时也记作 En 或 E 。 对称阵: T A = A 反对称阵: T A = -A 注1 行(列)矩阵通常称为行(列)向量。并习惯用小写字母表示,其每一元素称为分量。 分量个数称为维数。 注2 上述所列的特殊矩阵,除零矩阵、行或列矩阵外,均为方阵。 注3 对反对称阵 ( ) A = aij 来说,必有 a (i n) ii = 0 = 1,2,L 。 注4 任一方阵 A 均可表示为一个对称阵和一个反对称阵之和,即 ( ) ( ) T T A = A + A + A - A 2 1 2 1 1.1.2 矩阵的运算 (1) 加法:设 ( ) m n A aij ´ = , ( ) m n B bij ´ = ,则 ( ) m n A B aij bij ´ + = + (2) 数承:设 ( ) m n A aij ´ = ,k 为数,则 ( ) m n ij kA ka ´ = (3) 乘法:设 ( ) m s A aij ´ = , ( ) s n B bij ´ = ,则 ( ) m n ij AB c ´ = ,其中 C a b a b a b a b (i m j n) i j i j is sj s k ij ik kj 1 1 2 2 L 1,2,L ; 1,2,L 1 = å = + + = = = 注 两矩阵可乘的条件:左边矩阵的列数等于右边矩阵的行数。 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn
a1a2…aim [aa21…a (4)转置:设A= aan…a2n 称为A的转置,记作 A或N (5)运算规律 下表给出了矩阵与数的运算规律之比较, 运算 新 矩阵 说明 加法 a+b-bta A+B-B+A 能铭相加的矩阵 (a+b)+c-a+(b+c) (A+B)+C-A+(B+C) 必须是同维矩阵 a+0=a A+0=A 数乘 (ab)A=a(bA)=b(aA) a.b是数 (a+b)A=aA+bA A,B是同维矩阵 a(A+B)=aA+aB 乘 a*1=a A*I=A 要注意1的维数 】*a=a I'A=A (ab)c=a(bc) (AB)C=A(BC) A的列数须等于B的行 勒 B的列数须等于D的行 A(b+c)=ab+ac A(B+CEAB+AC B与C须同维,A的列 (b+c)d=bd+cd (B+C)D=BD+CD 数须等于B的行数,B 的列数须等于D的行 Ab-ba 般AB≠BA 阿 如 [10T1111 0o2F0 的ee 若k≠0, 且若 消去律一般不成立,但 ak=bk或(ka=b), K≠0(或L≠O)且KA=KB 当K(或L)可逆时, A=B必成立 则a=b (或AL=BL),一般A≠B aa=a A·A=A A必须是方阵,且k, 为非负整数 (ab)"=a'b 一般(AB)≠AB 当A,B为同阶方阵, 且AB=BA,k为非负 整数时, (AB)≠AB PDF文件使用”pdfFactory Pro”试用版本创建,fineprint,cn
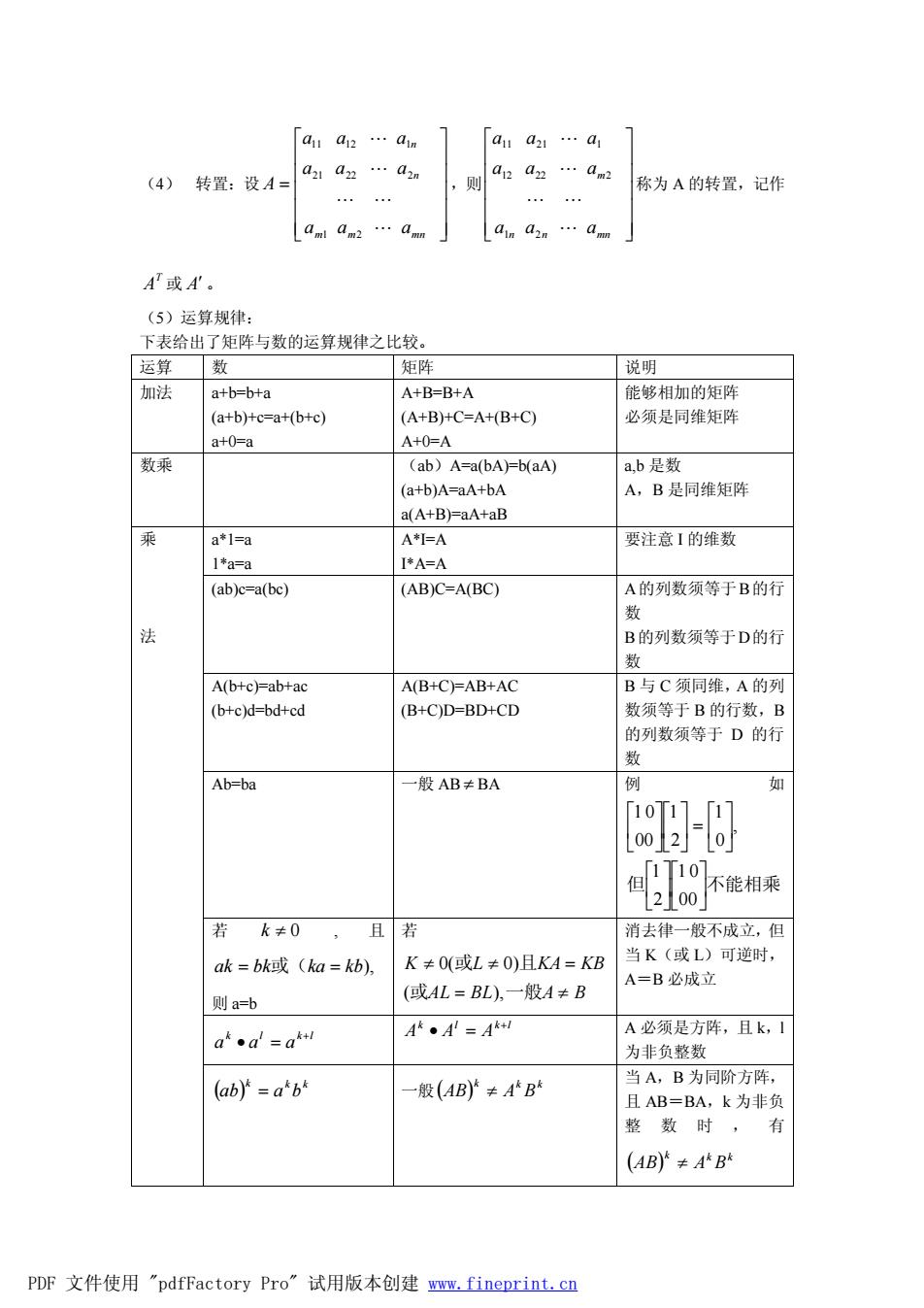
(4) 转置:设 ú ú ú ú ú û ù ê ê ê ê ê ë é = m m mn n n a a a a a a a a a A L L L L L 1 2 21 22 2 11 12 1 ,则 ú ú ú ú ú û ù ê ê ê ê ê ë é n n mn m a a a a a a a a a L L L L L 1 2 12 22 2 11 21 1 称为 A 的转置,记作 T A 或 A¢ 。 (5)运算规律: 下表给出了矩阵与数的运算规律之比较。 运算 数 矩阵 说明 加法 a+b=b+a (a+b)+c=a+(b+c) a+0=a A+B=B+A (A+B)+C=A+(B+C) A+0=A 能够相加的矩阵 必须是同维矩阵 数乘 (ab)A=a(bA)=b(aA) (a+b)A=aA+bA a(A+B)=aA+aB a,b 是数 A,B 是同维矩阵 a*1=a 1*a=a A*I=A I*A=A 要注意 I 的维数 (ab)c=a(bc) (AB)C=A(BC) A的列数须等于B的行 数 B的列数须等于D的行 数 A(b+c)=ab+ac (b+c)d=bd+cd A(B+C)=AB+AC (B+C)D=BD+CD B 与 C 须同维,A 的列 数须等于 B 的行数,B 的列数须等于 D 的行 数 Ab=ba 一般 AB ¹ BA 例 如 但 ú不能相乘 û ù ê ë é ú û ù ê ë é ú û ù ê ë é =ú û ù ê ë é ú û ù ê ë é 00 1 0 2 1 , 0 1 2 1 00 1 0 若 k ¹ 0 , 且 ak = bk或(ka = kb), 则 a=b 若 AL BL A B K L KA KB = ¹ ¹ ¹ = 或 一般 或 且 ( ), 0( 0) 消去律一般不成立,但 当 K(或 L)可逆时, A=B 必成立 k l k l a a a + · = k l k l A A A + · = A 必须是方阵,且 k,l 为非负整数 乘 法 ( ) k k k ab = a b 一般( ) k k k AB ¹ A B 当 A,B 为同阶方阵, 且 AB=BA,k 为非负 整 数 时 , 有 ( ) k k k AB ¹ A B PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

转置 (4Y=A A,B为同维矩阵, k为数 (A+B)=4+B A的列数须等于B的行 (kA)=kA (AB)=BA 1.13矩阵的初等变换与初等矩阵 (1)矩阵A的初等变换有如下三类 第一类:将A的第i行(列)与第j行(列)对换,记为,C): 第二类:以非零常数k乘A的i行(列),记作r(k)C,(k)。 第三类:将A的第i行(列的k倍加到第j行(列)上去,记作,化北k): (2)初等矩阵是单位阵1经过一次初等变换后得到的矩阵 1R,1RW,1因)R, 1S6,1c国e.1R (4)初等变换与初等矩阵之间的关系 (5)初等矩阵左(右)乘A,相当与对A进行一次相应的初等行(列)变换,例如: AB台R,AB,ASB台4C,=B. 注1若矩阵A经过有限次初等变换得到矩阵B,则称B与A等价,此时必有等式 R,…RAC,…C,=B成立,其中R,…R和C,…C,均为初等矩阵 注2任一矩阵A经有限次初等变换后均可化为形如[0]的矩阵,其中1为A的铁,称 L00 1.1.4可逆矩阵的定义 设A为n阶方阵,若存在n阶方阵B,使AB=BA=I,则称A为可逆矩阵,称B为A的你 矩阵。 注1可逆矩阵必是方阵。 注2A若为可逆,其逆必唯一,故A的呢矩阵记作A,即有 A4-=AA=I 注4可逆矩阵又称为非退化阵或非奇异阵或满秩阵,不可逆阵又称为退化阵或奇异阵或降 秩阵。 1.1.5可逆矩阵的性质 (1)若A可逆,则A,A均可逆,且(4=A,(A)~=(Ay PDF文件使用"pdfFactory Pro”试用版本创建,fineprint,cn
转置 ( ) ( ) ( ) ( ) T T T T T T T T T T AB B A kA kA A B A B A A = = + = + = A, B 为同维矩阵, k 为数 A的列数须等于B的行 数 1.1.3 矩阵的初等变换与初等矩阵 (1)矩阵 A 的初等变换有如下三类: 第一类:将 A 的第 i 行(列)与第 j 行(列)对换,记为 ( ) ij ij r c 。 第二类:以非零常数 k 乘 A 的 i 行(列),记作 r k (c (k )) i i ( ) 。 第三类:将 A 的第 i 行(列)的 k 倍加到第 j 行(列)上去,记作 r (k )(c (k )) ij ij 。 (2)初等矩阵是单位阵 I 经过一次初等变换后得到的矩阵 ij ij R r I ¾¾® , ( ) ( ) R k r k I i ¾¾ ® i ¾ , ( ) ( ) R k r k I ij ¾¾ij ¾® ij ij c c I ¾¾® , ( ) ( ) c k c k I i ¾¾i ¾® , ( ) ( ) R k c k I ij ¾¾ij ¾® (4) 初等变换与初等矩阵之间的关系 (5) 初等矩阵左(右)乘 A,相当与对 A 进行一次相应的初等行(列)变换,例如: B R AB r A ij ¾¾®ij Û , B AC B c A ij ij ¾¾® Û = 。 注 1 若矩阵 A 经过有限次初等变换得到矩阵 B,则称 B 与 A 等价,此时必有等式 Rs LR1AC1LCt = B 成立,其中 Rs LR1 和C1LCt 均为初等矩阵。 注 2 任一矩阵 A 经有限次初等变换后均可化为形如 ú û ù ê ë é 0 0 0 r I 的矩阵,其中 r 为 A 的秩,称 矩阵 ú û ù ê ë é 0 0 0 r I 为 A 的标准型。 1.1.4 可逆矩阵的定义 设 A 为 n 阶方阵,若存在 n 阶方阵 B,使 AB=BA=I,则称 A 为可逆矩阵,称 B 为A的你 矩阵。 注 1 可逆矩阵必是方阵。 注 2 A 若为可逆,其逆必唯一,故 A 的呢矩阵记作 -1 A ,即有 AA = A A = I -1 -1 注4 可逆矩阵又称为非退化阵或非奇异阵或满秩阵,不可逆阵又称为退化阵或奇异阵或降 秩阵。 1.1.5 可逆矩阵的性质 (1)若 A 可逆,则 T A , -1 A 均可逆,且(A ) = A - - 1 1 , ( ) T T A A 1 1 ( ) - - = PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

2)若A可递,数长0,则可地,且一 (3)若A,B是同阶可逆阵,则AB可逆,且(AB=B-A 注若A,B为同阶的可逆矩阵,则A十B不一定可逆。 1.1.6可逆矩阵的判别方法 (I)利用定义:若AB=BA=,则必有A可逆,且A=B。 (2)利用行列式:若「A≠0,则A可逆。 (3)利用性质(3):将矩阵分解成可逆矩阵的乘积。 (4)利用矩阵的秩:A为n阶方阵,若()=n,则A可逆。 (5)利用线性方程组:若n×n方程组Ar=b有唯一解,则A可逆。 (6)利用向量组的线性无关性:若方阵A的行(或列)向量线性无关,则A可逆。 (7)利用初等矩阵:若A可分解为有限个初等矩阵之积,则A可逆。 (8) 利用特 :证明数零不是A的特征值,则A可逆, (9)利用反证法:这是常用方法。 注1方法(1)在具体使用时,实际上只需验证AB=I或BA=I,即两者只要有一个成立 时,就必有A=B,当然此时A,B必须是同阶矩阵。 注2初等矩阵都是可逆阵,且其逆也是初等矩阵 (心=见风因=只得=风人小.因此,对任矩库九多存在可 逆阵P,Q,使PAQ= 「1,01 00 ,这称为A的标准分解。 注3方法(7)说明可逆阵必与单位阵等价,这一结论也是我们利用初等变换求逆矩阵的 理论依据。 1.1.7逆矩阵的计算方法 (1)利用初等变换 aI)五1合)别化】 注(1))行14)只能用行初等变换 (份列化)小只监用列脚等表换 PDF文件使用"pdfFactory Pro”试用版本创建,fineprint.cn
(2)若 A 可逆,数 k ¹ 0 ,则 kA 可逆,且 1 1 1 ( ) - - = A k kA (3) 若 A,B 是同阶可逆阵,则 AB 可逆,且( ) -1 -1 -1 AB = B A 注 若 A,B 为同阶的可逆矩阵,则 A+B 不一定可逆。 1.1.6 可逆矩阵的判别方法 (1) 利用定义:若 AB=BA=I,则必有 A 可逆,且 A = B -1 。 (2) 利用行列式:若 éAù ¹ 0,则 A 可逆。 (3) 利用性质(3):将矩阵分解成可逆矩阵的乘积。 (4) 利用矩阵的秩:A 为 n 阶方阵,若 r(A) = n,则 A 可逆。 (5) 利用线性方程组:若 n´ n 方程组 Ax = b 有唯一解,则 A 可逆。 (6) 利用向量组的线性无关性:若方阵 A 的行(或列)向量线性无关,则 A 可逆。 (7) 利用初等矩阵:若 A 可分解为有限个初等矩阵之积,则 A 可逆。 (8) 利用特征值:证明数零不是 A 的特征值,则 A 可逆。 (9) 利用反证法:这是常用方法。 注1 方法(1)在具体使用时,实际上只需验证 AB=I 或 BA=I,即两者只要有一个成立 时,就必有 A = B -1 ,当然此时 A,B 必须是同阶矩阵。 注2 初 等 矩 阵 都 是 可 逆 阵 , 且 其 逆 也 是 初 等 矩 阵 ( ( ) R ( ) k R ( k ) k Rij Rij Ri k Ri ÷ ij = ij - ø ö ç è æ = = -1 -1 -1 , 1 , ),因此,对任一矩阵 A,必存在可 逆阵 P,Q,使 ú û ù ê ë é = 0 0 0 r I PAQ ,这称为 A 的标准分解。 注3 方法(7)说明可逆阵必与单位阵等价,这一结论也是我们利用初等变换求逆矩阵的 理论依据。 1.1.7 逆矩阵的计算方法 (1) 利用初等变换 ( ) ( ) 1 | | 行 - A I ¾¾® I A 或 ÷ ÷ ø ö ç ç è æ ÷ ÷ ¾¾® ø ö ç ç è æ 1 I A - 列 A I 注 ( ) ( ) 1 | | 行 - A I ¾¾® I A 只能用行初等变换 ÷ ÷ ø ö ç ç è æ ÷ ÷ ¾¾® ø ö ç ç è æ 1 I A - 列 A I 只能用列初等变换 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

(2)利用伴随阵 注在具体计算时这一公式适用于较低阶的矩阵 (3)利用分块矩阵 (4)凑法:当条件中有矩阵方程时,通过矩阵运算规律从矩阵方程中凑出AB=I的形式, 从而可得A=B,这一方法适用于抽象矩阵求逆。 1.1.8分块矩阵的定义于运算 (1)定义 用若干条纵线和横线把一个矩阵分成若干个小块。每一小块称为矩阵的一个子块和 子矩阵,则一这些子块为元素的原矩阵称为分块矩阵, (2)运算 (3)进行分块矩阵的加、减、乘法和转置运算,可降子矩阵当作通常矩阵的元素看待。 注1同维矩阵,只有用同样的分块方法时,才能进行分块相加。 这2分块乘法只有当左边矩阵分法于右边矩阵的行分法一致时才能进行。 注4分块转置除了行列互换外,每一子块也需转置,即若 AA2…A 4=4…4, ::: AA2…An 则 「AA…A 4T= A站A品…A AA…A 1.1.9利用分块矩阵求逆矩阵 (1)对分块对角阵 A 若A,=1,2,…,s)可逆,则A可逆且 PDF文件使用"pdfFactory Pro”试用版本创建,fineprint,cn
(2) 利用伴随阵 A A A * 1 = - 注 在具体计算时这一公式适用于较低阶的矩阵 (3) 利用分块矩阵 (4) 凑法:当条件中有矩阵方程时,通过矩阵运算规律从矩阵方程中凑出 AB=I 的形式, 从而可得 A = B -1 ,这一方法适用于抽象矩阵求逆。 1.1.8 分块矩阵的定义于运算 (1) 定义 用若干条纵线和横线把一个矩阵分成若干个小块。每一小块称为矩阵的一个子块和 子矩阵,则一这些子块为元素的原矩阵称为分块矩阵。 (2) 运算 (3) 进行分块矩阵的加、减、乘法和转置运算,可降子矩阵当作通常矩阵的元素看待。 注 1 同维矩阵,只有用同样的分块方法时,才能进行分块相加。 这 2 分块乘法只有当左边矩阵分法于右边矩阵的行分法一致时才能进行。 注4 分块转置除了行列互换外,每一子块也需转置,即若 ú ú ú ú û ù ê ê ê ê ë é = s s sr r r A A A A A A A A A A L M M M L L 1 2 21 22 2 11 12 1 则 ú ú ú ú ú û ù ê ê ê ê ê ë é = T sr T r T r T s T T T s T T T A A A A A A A A A A L M M M L L 1 2 12 22 2 11 21 1 1.1.9 利用分块矩阵求逆矩阵 (1) 对分块对角阵 ú ú ú ú û ù ê ê ê ê ë é = As A A A O 2 1 若 Ai (i = 1,2,L,s)可逆,则 A 可逆且 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn
(2)对 A 若A,=1,2,,s)可逆,则A可逆且 A (3)对 4 D C 其中B为m×m可逆阵,C为n×n可逆阵,则A可逆,且 哦4 07 o C L-C-DB C 注当矩阵的零元素较多时,可考虑分块,时告诚矩阵的运算转化为低阶矩阵的运算,这是 简化矩阵运算的一个途径。 1.1.10用列(行)方块易推得的一些结论 (1)将A按列分块 a1a2…am A= a1am…an =a,a2,…,an] dd2…am 其中a,是A的第j列,则 Ae,=a,U=1,2,…nm PDF文件使用"pdfFactory Pro”试用版本创建,fineprint.cn
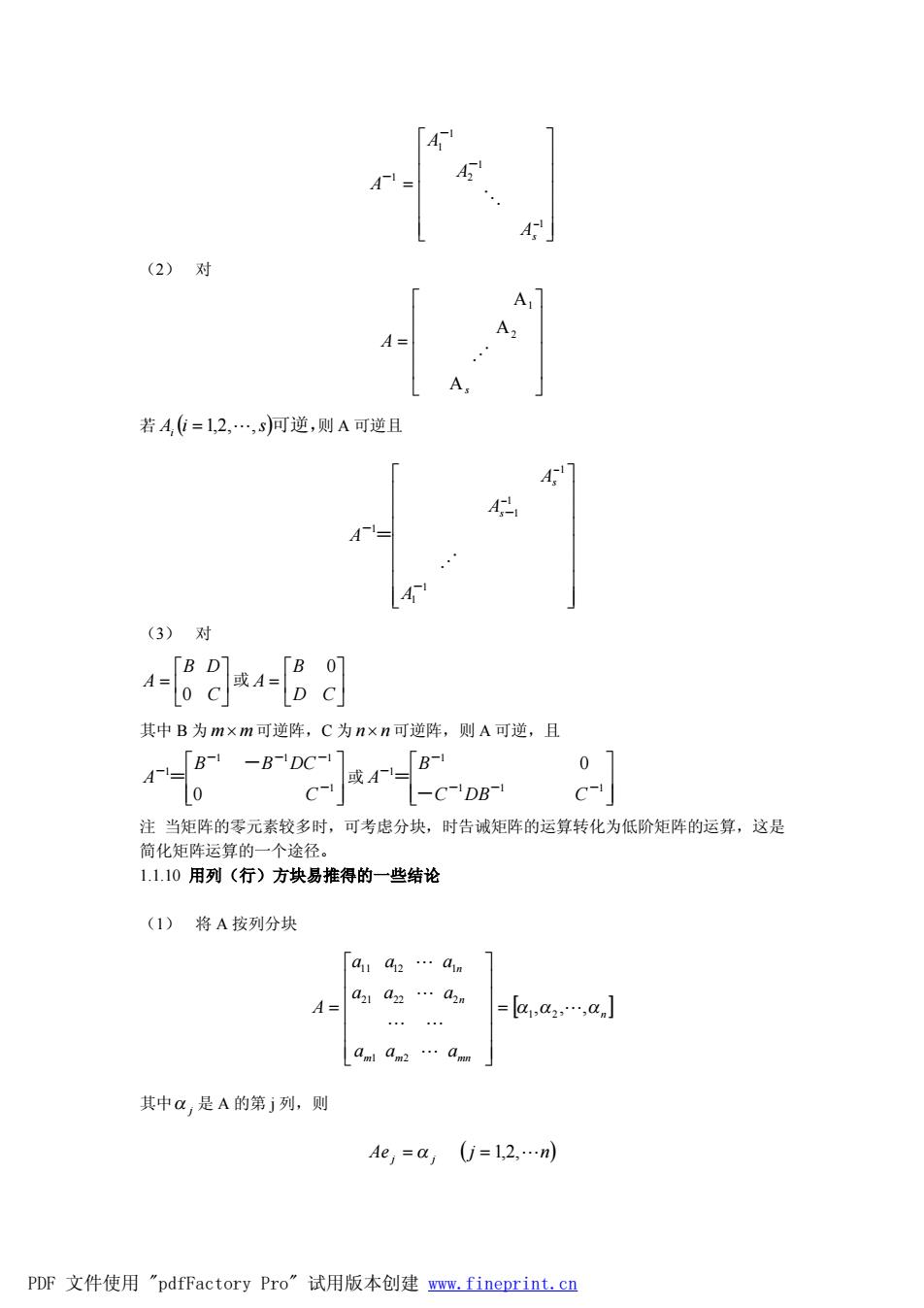
ú ú ú ú ú û ù ê ê ê ê ê ë é = -1 1 2 1 1 1 As A A A O - - - (2) 对 ú ú ú ú û ù ê ê ê ê ë é = s A A A A 2 1 N 若 Ai (i = 1,2,L,s)可逆,则 A 可逆且 ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ë é - - 1 1 1 1 1 1 - - - = A A A A s s N (3) 对 ú û ù ê ë é = C B D A 0 或 ú û ù ê ë é = D C B A 0 其中 B 为 m´ m可逆阵,C 为 n´ n 可逆阵,则 A 可逆,且 ú ú û ù ê ê ë é 1 1 1 1 1 0 - - - - - - = C B B DC A 或 ú ú û ù ê ê ë é 1 1 1 1 1 0 - - - - - - = C DB C B A 注 当矩阵的零元素较多时,可考虑分块,时告诫矩阵的运算转化为低阶矩阵的运算,这是 简化矩阵运算的一个途径。 1.1.10 用列(行)方块易推得的一些结论 (1) 将 A 按列分块 [ ] n m m mn n n a a a a a a a a a A a1 ,a2 , ,a 1 2 21 22 2 11 12 1 L L L L L L = ú ú ú ú ú û ù ê ê ê ê ê ë é = 其中a j 是 A 的第 j 列,则 Ae ( j n) j = a j = 1,2,L PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn